
第十五章食品分析中的质量保证 食品分析的结果是许多重要决策的基础 如,食品企业根据原辅材料的分析结果决定 接受还是拒受:根据加工过程中各个关健控制点的在线检测结果,了解食品安全控制状态 决定是否需要采取预防或纠偏措施:根据终产品的分析结果决定某批次产品是否合格,能否 放行出厂,进入食品流通渠道。又如,相关政府机构根据食品分析结果进行食品质量与安全 方面的监督和管理,以保护消费者健康。维护消费者合法权荟。总而言之,食品分析结果的 质量直接影响生产、科研、司法等重要活。 实践证明 如果没有可靠的分析质量保证措施 就不能提供可靠的分析数据,由此造成的后果可能会比没有数据更为严重。另 一方面,分利 人员本身也常常面临证明其分析结果的准确性或可靠性的压力,需要用分析质量保证体系来 证明其有能力提供符合质量要求的分析结果。所以,分析质量保证对食品企业、食品科学研 究机构、食品质量与安全管理机构以及分析人员都具有十分重要的意义。 分析质量保证(Ana ytical AQA)指分析测试过程中,为了将各种误 差减少到预期要求而采取一系列培训、能力测 、控制、监督 ,审核 认证等措施的过稻 因此,分析质量保证涉及许多影响分析结果的因素,例如,分析测试中使用仪器设备的性能 玻璃量器的准确性、试剂的质量、分析测量环境和条件、分析人员的素质和技术熟练程度、 采样的代表性以及选用分析方法的灵敏度等等。由于整个分析过程比较复杂,不可能做到完 于缺,日题中任何 一个环节发生问趣,就一定会影响测定结果的准确性,产生测量误差 虽然,随若现代科学技术水平以及分析人员素质的提高 可以将误差控制在比较小的范围内 但是,不论分析人员怎样努力,都不可能彻底消除分析过程中的误差。所以,分析质量保证 是一个需要不断改进与完善的过程。 本章将从如何保证分析数据的质量、如何进行实验室质量控制等方面,阐述食品分析 中质量保证的主要内容 第一节 分析数据的质量 分析人员和利益相关各方都非常关心分析过程和分析结果是否有效和可信,或者说分积 结果的质量如何。对分析结果(即分析数据)的可信程度提出疑问是很自然的,因为人们需 要比较、评价或再现(复现)分析结果。但是,回答这些问题存在一定的难度,因为,影响 测定结果的因素很多,而人们对各影响因素又缺乏全面的了解。在实际工作中,尽管分析人 员选择最准确的分析方法、使 用最精密的仪器设备,具各丰富的经验和熟练的技术 对同 样品进行多次重复分析,也不会获得完全相同的结果,更不可能得到绝对准确的结果。这就 表明,误差是客观存在的。如何减少分析过程中的误差,减少分析数据的不确定度,是保证 分析数据质量的关键措施。 误差或测量误差是指测量值或测量结果与真实值之间的差异。根据误差的性质,误差可 分为系统误差、偶然误差和过失误差三大类。 (1)系统误差 系统误差是由分析过程中某些周定原因造成的,使测定结果系统地偏高或偏低。常见 的系统误差根据其性质和产生的原因,可将其分为方法误差、仪器误差、试剂误差、操作误 差(或主观误差)等几种。 (2)偶然误若 偶然误差又称随机误差。它是由某些难以控制、无法避免的偶然因素造成的,其大小 与正负值都不固定,又称不定误差。偶然误差的产生难以找到确定的原因,似乎没有规律性。 1
1 第十五章 食品分析中的质量保证 食品分析的结果是许多重要决策的基础。如,食品企业根据原辅材料的分析结果决定 接受还是拒受;根据加工过程中各个关键控制点的在线检测结果,了解食品安全控制状态, 决定是否需要采取预防或纠偏措施;根据终产品的分析结果决定某批次产品是否合格,能否 放行出厂,进入食品流通渠道。又如,相关政府机构根据食品分析结果进行食品质量与安全 方面的监督和管理,以保护消费者健康,维护消费者合法权益。总而言之,食品分析结果的 质量直接影响生产、科研、司法等重要活动。实践证明,如果没有可靠的分析质量保证措施, 就不能提供可靠的分析数据,由此造成的后果可能会比没有数据更为严重。另一方面,分析 人员本身也常常面临证明其分析结果的准确性或可靠性的压力,需要用分析质量保证体系来 证明其有能力提供符合质量要求的分析结果。所以,分析质量保证对食品企业、食品科学研 究机构、食品质量与安全管理机构以及分析人员都具有十分重要的意义。 分析质量保证(Analytical Quality Assurance, AQA)指分析测试过程中,为了将各种误 差减少到预期要求而采取一系列培训、能力测试、控制、监督、审核、认证等措施的过程。 因此,分析质量保证涉及许多影响分析结果的因素,例如,分析测试中使用仪器设备的性能、 玻璃量器的准确性、试剂的质量、分析测量环境和条件、分析人员的素质和技术熟练程度、 采样的代表性以及选用分析方法的灵敏度等等。由于整个分析过程比较复杂,不可能做到完 美无缺,只要其中任何一个环节发生问题,就一定会影响测定结果的准确性,产生测量误差。 虽然,随着现代科学技术水平以及分析人员素质的提高,可以将误差控制在比较小的范围内, 但是,不论分析人员怎样努力,都不可能彻底消除分析过程中的误差。所以,分析质量保证 是一个需要不断改进与完善的过程。 本章将从如何保证分析数据的质量、如何进行实验室质量控制等方面,阐述食品分析 中质量保证的主要内容。 第一节 分析数据的质量 分析人员和利益相关各方都非常关心分析过程和分析结果是否有效和可信,或者说分析 结果的质量如何。对分析结果(即分析数据)的可信程度提出疑问是很自然的,因为人们需 要比较、评价或再现(复现)分析结果。但是,回答这些问题存在一定的难度,因为,影响 测定结果的因素很多,而人们对各影响因素又缺乏全面的了解。在实际工作中,尽管分析人 员选择最准确的分析方法、使用最精密的仪器设备,具备丰富的经验和熟练的技术,对同一 样品进行多次重复分析,也不会获得完全相同的结果,更不可能得到绝对准确的结果。这就 表明,误差是客观存在的。如何减少分析过程中的误差,减少分析数据的不确定度,是保证 分析数据质量的关键措施。 一、误差 误差或测量误差是指测量值或测量结果与真实值之间的差异。根据误差的性质,误差可 分为系统误差、偶然误差和过失误差三大类。 (1)系统误差 系统误差是由分析过程中某些固定原因造成的,使测定结果系统地偏高或偏低。常见 的系统误差根据其性质和产生的原因,可将其分为方法误差、仪器误差、试剂误差、操作误 差(或主观误差)等几种。 (2)偶然误差 偶然误差又称随机误差。它是由某些难以控制、无法避免的偶然因素造成的,其大小 与正负值都不固定,又称不定误差。偶然误差的产生难以找到确定的原因,似乎没有规律性

但如果进行很多次测量,就会发现其服从正态分布规律。偶然误差在分析操作中是不可避免 的。 (3)过失误差 分析工作中除上述两类误差外,还有一类“过失误差”。它是由于分析人员粗心大意或 未按操作规程办事所造成的误差。在分析工作中,当出现误差值很大时,应分析其原因,如 是过失误差引起的,则该结果应舍去。 、不确定度 1完义 不确定度是测量不确定度的简称 ,指对分析结果的正确性或准确性的可疑程度。不确 定度是用于表达分析质量优劣的一个指标,是合理地表征测量值或其误差离散程度的一个参 数。 不确定度又叫可疑程度,习惯地俗称为“不可靠程度”。它定量地表述了分析结果的可可 疑程度,定量地说明了实验室(包括所用设备和条件)分析能力水平。因此,常作为计量认 质量认证以及实验室认可等活动的重要依据 一。另外, 通常真实值是未知的, 析结果是分析组分真实值的一个估计值。只有在得到不确定度值后,才能衡量分析所得数据 的质量,才能指导数据在技术、商业、安全和法律方面的应用。 2分类 不确定度是与分析结果有关的参数,在分析结果的完整表述中,应句括不确定度。不 确定度可以用标准差或其倍数,或是一定置信水平下的区间(置信 间) 来表示,因此就可 将不确定度分为两大类:标准不确定度和扩展不确定度。 (1)标准不确定度 用标准偏差表示的分析结果的不确定度。根据计算方法,标准不确定度又分为三类。A 类标准不确定度是用统计分析方法计算的不确定度:B类标准不确定度是用不同于A类的 其他方法计算的,以估计的标准差表示:而所有标准不确定度分量的合成称为合 成标准不确 定度, 其标准偏差也是 估计值 (2)扩展不确定用 扩展不确定度又称为总不确定度。它提供了一个区间。分析值以一定的置信水平落在这 个区间内。扩展不确定度一般是这个区间的半宽。 不确定府分类如下 「A类标准不确定度 标准不确定度B类标准不确定度 不确定度」 合成标准不确定度 扩展不确定度 3来源 在实际分析工作中,分析结果的不确定度来源于很多方面,典型的来源包括:对样品 的定义不完整或不完善:分析的方法不理想:取样的代表性不够:对分析过程中环境影响的 认识不周全,或对环境条件的控制不完善:对仪器的读数存在偏差:分析仪器计量性能(灭 敏度、分辨力、稳定性等)上的局限性:标准物质的标准值不准确:引进的数据或其他参量 的不确定度:与分析方法和分析程序有关的近似性和假定性:在表面上看来完全相同的条件 下,分析时重观测估的弯化签 典型的不确定度源包括 (1)取样 分析过程中在实验室或现场取样时,取样代表性不够、不同样品间的随机变化和在取样 过程中潜在的偏差可导致最终结果的不确定度。 2
2 但如果进行很多次测量,就会发现其服从正态分布规律。偶然误差在分析操作中是不可避免 的。 (3)过失误差 分析工作中除上述两类误差外,还有一类“过失误差”。它是由于分析人员粗心大意或 未按操作规程办事所造成的误差。在分析工作中,当出现误差值很大时,应分析其原因,如 是过失误差引起的,则该结果应舍去。 二、不确定度 1.定义 不确定度是测量不确定度的简称,指对分析结果的正确性或准确性的可疑程度。不确 定度是用于表达分析质量优劣的一个指标,是合理地表征测量值或其误差离散程度的一个参 数。 不确定度又叫可疑程度,习惯地俗称为“不可靠程度”。它定量地表述了分析结果的可 疑程度,定量地说明了实验室(包括所用设备和条件)分析能力水平。因此,常作为计量认 证、质量认证以及实验室认可等活动的重要依据之一。另外,由于通常真实值是未知的,分 析结果是分析组分真实值的一个估计值。只有在得到不确定度值后,才能衡量分析所得数据 的质量,才能指导数据在技术、商业、安全和法律方面的应用。 2.分类 不确定度是与分析结果有关的参数,在分析结果的完整表述中,应包括不确定度。不 确定度可以用标准差或其倍数,或是一定置信水平下的区间(置信区间)来表示,因此就可 将不确定度分为两大类:标准不确定度和扩展不确定度。 (1) 标准不确定度 用标准偏差表示的分析结果的不确定度。根据计算方法,标准不确定度又分为三类。A 类标准不确定度是用统计分析方法计算的不确定度;B 类标准不确定度是用不同于 A 类的 其他方法计算的,以估计的标准差表示;而所有标准不确定度分量的合成称为合成标准不确 定度,其标准偏差也是一个估计值。 (2) 扩展不确定度 扩展不确定度又称为总不确定度。它提供了一个区间,分析值以一定的置信水平落在这 个区间内。扩展不确定度一般是这个区间的半宽。 不确定度分类如下: A 类标准不确定度 标准不确定度 B 类标准不确定度 不确定度 合成标准不确定度 扩展不确定度 3.来源 在实际分析工作中,分析结果的不确定度来源于很多方面,典型的来源包括:对样品 的定义不完整或不完善;分析的方法不理想;取样的代表性不够;对分析过程中环境影响的 认识不周全,或对环境条件的控制不完善;对仪器的读数存在偏差;分析仪器计量性能(灵 敏度、分辨力、稳定性等)上的局限性;标准物质的标准值不准确;引进的数据或其他参量 的不确定度;与分析方法和分析程序有关的近似性和假定性;在表面上看来完全相同的条件 下,分析时重复观测值的变化等。 典型的不确定度源包括: (1) 取样 分析过程中在实验室或现场取样时,取样代表性不够、不同样品间的随机变化和在取样 过程中潜在的偏差可导致最终结果的不确定度

(2)存放冬件 实验样品在分析前要存放一段时间,存放条件可能影响结果。存放期限和存放条件应 该作为不确定度源加以考虑。 如分析天平校准的准确度范围,温度控制器可能保持与它的指示设定点不同的平均温 度,自动分析仪可能有滞后效应等。 (4)式体度 即使已测定了试剂的纯府,试剂溶液的浓度仍不能准确知道,因为与测定过程有关的 (5)假定的化学计算 一般分析时都要假定分析过程遵循一个特殊反应的化学计算,但这一化学计算和实际的 计算还是有差异的,而且还可能发生了不完全反应或剧反应。 (6)分析条件 如分析环境温度有时会影响到分析结 ,要考虑到温度的不确定度,当然,显著的温月 效应必须校正。同样,在样品对可能的湿度变化敏感的情况下,湿度也会引起分析结果的不 确定度。 (7)样品效应 复杂的样品中被分析成分的回收率或仪器响应可能受到样品组成的影响,被分析成分 可能 步复合这种影响。由于复杂的成分改变了热状态或光分解效应,样品和被分析成分 的稳定性在分析中也会发生变化。 (8)计算上的影响 选择的校准模式,如对曲线的响应选择直线校准,可能会导致较大的不确定度:舍项也 可能会导致结果不准确。 (9 空白校正 空白值和空白矫正的合理性均存在不确定度,这在痕量分析中特别重要, (10)分析人员的影明 读数可能偏高或偏低 (11)随机效应 所有分析中都有随机因素响产生的不确定度 4,不确定度的评估过程 不确定度的评估在原理上很简单。下面叙述了为获取分析结果的不确定度估计值所要 进行的工作。这些步骤包括: (1)规定分析对象 清楚地写明需要分析什么,包括分折对象和分析所依赖的输入量倒如所测定的参教、 常数、校准标准值等)的关系。只要可偷 ,还应该包括对已知系统影响量的修正。该技术 定资料应在有关的标准操作程序(SOP)或其他方法描述中给出。 (2) 识别不确定度的可能来源 列出不确定度的可能来源。包括第一步所规定的关系式中所含参数的不确定度来源, 但是也可以有其他来源,必须句括那些由化学霞设所生的不确定度来源。 (3)不确定度分最的量化 测量或估计与所识别的每 一个潜在的不确定度来源相关的不确定分量的大小。通常能 评估或测量与大量独立来源有关的不确定度的单个分量,要考虑数据是否足以反映所有的不 确定度来源,计划其他的实验和研究来保证所有的不确定度来源都得到充分的考虑。 3
3 (2) 存放条件 实验样品在分析前要存放一段时间,存放条件可能影响结果。存放期限和存放条件应 该作为不确定度源加以考虑。 (3) 仪器效应 如分析天平校准的准确度范围,温度控制器可能保持与它的指示设定点不同的平均温 度,自动分析仪可能有滞后效应等。 (4) 试剂纯度 即使已测定了试剂的纯度,试剂溶液的浓度仍不能准确知道,因为与测定过程有关的 不确定度仍存在。而有些试剂在放置过程中也会发生纯度的变化。如氢氧化钠试剂和氢氧化 钠溶液在放置过程中都会和空气中的二氧化碳反应生成碳酸氢钠,纯度发生了变化。 (5) 假定的化学计算 一般分析时都要假定分析过程遵循一个特殊反应的化学计算,但这一化学计算和实际的 计算还是有差异的,而且还可能发生了不完全反应或副反应。 (6) 分析条件 如分析环境温度有时会影响到分析结果,要考虑到温度的不确定度,当然,显著的温度 效应必须校正。同样,在样品对可能的湿度变化敏感的情况下,湿度也会引起分析结果的不 确定度。 (7) 样品效应 复杂的样品中被分析成分的回收率或仪器响应可能受到样品组成的影响,被分析成分 可能进一步复合这种影响。由于复杂的成分改变了热状态或光分解效应,样品和被分析成分 的稳定性在分析中也会发生变化。 (8) 计算上的影响 选择的校准模式,如对曲线的响应选择直线校准,可能会导致较大的不确定度;舍项也 可能会导致结果不准确。 (9) 空白校正 空白值和空白矫正的合理性均存在不确定度,这在痕量分析中特别重要。 (10) 分析人员的影响 读数可能偏高或偏低。 (11) 随机效应 所有分析中都有随机因素响产生的不确定度。 4.不确定度的评估过程 不确定度的评估在原理上很简单。下面叙述了为获取分析结果的不确定度估计值所要 进行的工作。这些步骤包括: (1)规定分析对象 清楚地写明需要分析什么,包括分析对象和分析所依赖的输入量(例如所测定的参数、 常数、校准标准值等)的关系。只要可能,还应该包括对已知系统影响量的修正。该技术规 定资料应在有关的标准操作程序(SOP)或其他方法描述中给出。 (2) 识别不确定度的可能来源 列出不确定度的可能来源。包括第一步所规定的关系式中所含参数的不确定度来源, 但是也可以有其他来源,必须包括那些由化学假设所产生的不确定度来源。 (3)不确定度分量的量化 测量或估计与所识别的每一个潜在的不确定度来源相关的不确定分量的大小。通常能 评估或测量与大量独立来源有关的不确定度的单个分量。要考虑数据是否足以反映所有的不 确定度来源,计划其他的实验和研究来保证所有的不确定度来源都得到充分的考虑

(4)计算合成不确定度 在第三步中得到的信息是总不确定度的一些量化分量,它们可能与单个来源有关,也 可能与几个不确定度来源的合成影响有关。这些分量必须以标准偏差 的形式表 并根据 关规则进行合成,以得到合成标准不确定度。应使用适当的包含因子来给出扩展不确定度。 图151表示不确定度的评估过程。 二、误差和不确定度 误差和不确定度是两个完全不同的概念。误差是本,没有误差,就没有误差的分布,就 无法估计分布的标准偏差,当然也就不会有不确定度了。而不确定分析实质上是误差分析中 对误差分布的分析。然面,误差分析更具广义性,包含的内容更多 ,如系统误差的消除与减 胡等。可见,误差和不确定度紧密相关,但也有区别,其具体区别见表15-1。 表15-1误差与不确定度的主要区别 序号 误差 不流定 单一估 区间形式,可用于其所描述的所有分析位 2 表示分析结果相对真实值的偏离 表示分析结果的离散性 有正号或负号,其值为分析结果减去无符号的参数,用标准差或标准差的倍数 真实值 或置信区间的半宽表示 客观存在,不以人的认识程度而改变 与人们对分析对象 影响因素及分析过稻 4 的认识有关 由于真实值未知,往往不能准确得到,可以由人们根据实验、资料、经验等信息 5 当用约定真实值代替真实值时,可以进行评定,从而可以定量估计。评定方法 得到其估计值 有A和B两类 按性质可分为随机误差、系统误差和 不确定度分量评定时一般不必区分其性 过失误差三类。定义随机误差和系纷 质,若需要区分时应表述为:“由随机效 6. 误差都是无穷多次分析情况下的理想引入的不确定度分量”和“由系统效应 概念 入的不确定度分量” 己知系统误差的估计值时可以对分析不能用不确定度对分析结果进行正,在 7 结果进行修正。得到已修正的分析结 己修正分析结果的 下确定度中应考虑修 果 不完善而引入的不确定度 四、如何提高分折结果的准确度,减少不确定度 分析结果的准确度是指分析结果与真实值之间的一致程度。在定量分析工作中,为了使 分析结果和数据有意义,就要尽量提高分析结果的准确度。因此,定量分析必须对所测的数 据进行归纳、 取 舍等一系列分析处理(见第十六章): 同时,还需根据具体分析任务对准确 度的要求,合理判 和正 表述分析结果的可靠性与精密度以及分析的不确定度。 为此, 析人员应:该了解分析过程中产生误差的原因及误差出现的规律,并采取相应的措施碱小误 差,使分析结果尽量地接近客观的真实值。 从前面有关误差的讨论中可知,在分析测试过程中,不可避免地存在误差和不确定度。 那么如何尽可能地减小分析误差和分析的不 确定度,提高分析结果的准确度呢?下面结合实 际情况简单地予以讨论。 1选择合适的分析方法 各种分析方法的准确度和灵敏度是不同的,在实际工作中要根据具体情况和要求来选择 分析方法。化学分析法中的重量分析和滴定分析相对于仪器分析而言,准确度高,但灵敏度 低,话用于质量分数高的组分的测定。而仪墨分析方法相对而言灵敏度高,准确度低,因此 它适于质量分数低的组分的测 例如有 试样铁的质量分数为40, 10%,若用重铬酸钾法 滴定铁,其方法的相对误差为士02%,则铁的质量分数范用是40.02%~40.18%。若采用分
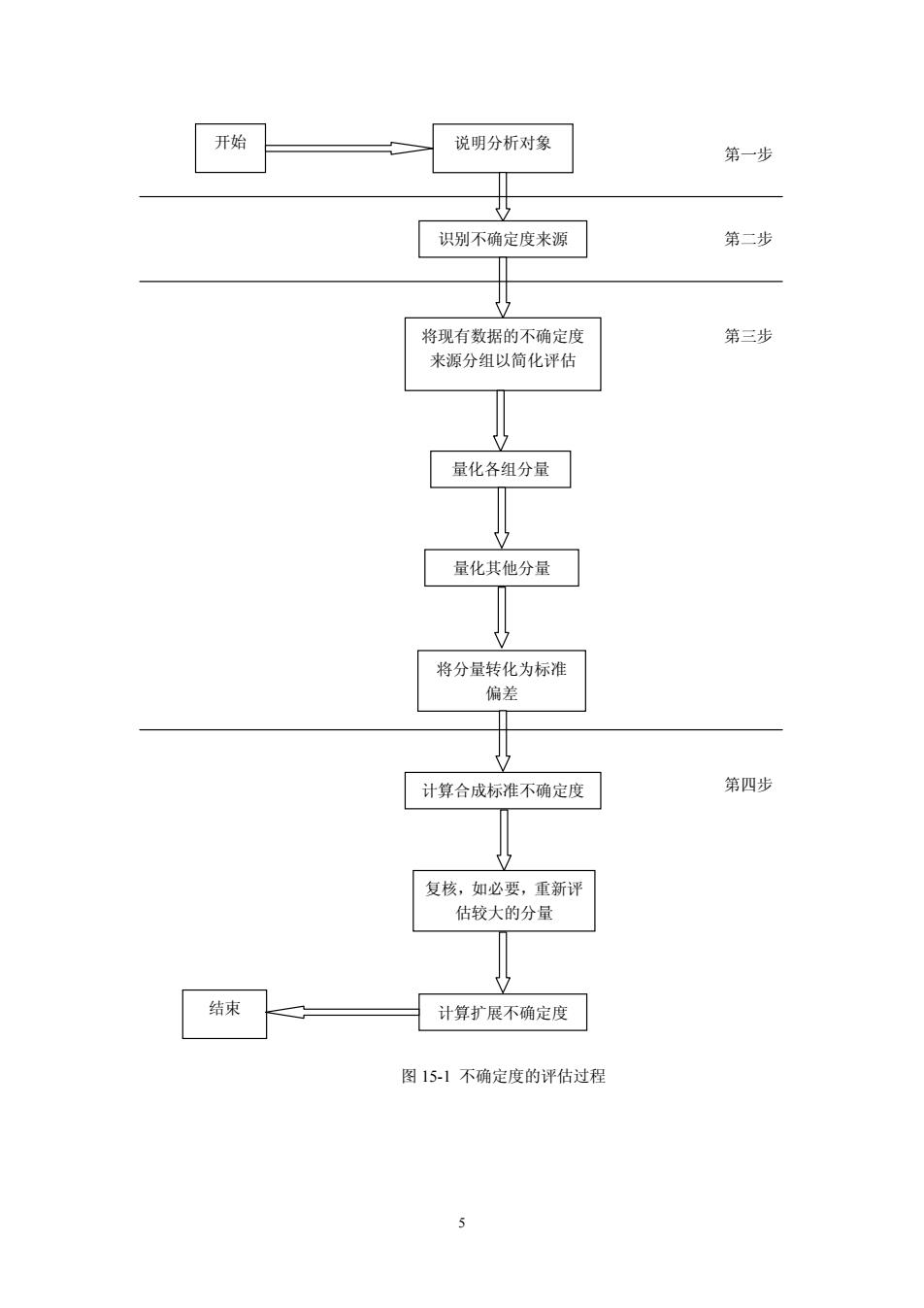
4 (4)计算合成不确定度 在第三步中得到的信息是总不确定度的一些量化分量,它们可能与单个来源有关,也 可能与几个不确定度来源的合成影响有关。这些分量必须以标准偏差的形式表示,并根据有 关规则进行合成,以得到合成标准不确定度。应使用适当的包含因子来给出扩展不确定度。 图 15-1 表示不确定度的评估过程。 三、误差和不确定度 误差和不确定度是两个完全不同的概念。误差是本,没有误差,就没有误差的分布,就 无法估计分布的标准偏差,当然也就不会有不确定度了。而不确定分析实质上是误差分析中 对误差分布的分析。然而,误差分析更具广义性,包含的内容更多,如系统误差的消除与减 弱等。可见,误差和不确定度紧密相关,但也有区别,其具体区别见表 15-1。 表 15-1 误差与不确定度的主要区别 序号 误差 不确定度 1 单一值 区间形式,可用于其所描述的所有分析值 2 表示分析结果相对真实值的偏离 表示分析结果的离散性 3 有正号或负号,其值为分析结果减去 真实值 无符号的参数,用标准差或标准差的倍数 或置信区间的半宽表示 4 客观存在,不以人的认识程度而改变 与人们对分析对象、影响因素及分析过程 的认识有关 5 由于真实值未知,往往不能准确得到, 当用约定真实值代替真实值时,可以 得到其估计值 可以由人们根据实验、资料、经验等信息 进行评定,从而可以定量估计。评定方法 有 A 和 B 两类 6 按性质可分为随机误差、系统误差和 过失误差三类。定义随机误差和系统 误差都是无穷多次分析情况下的理想 概念 不确定度分量评定时—般不必区分其性 质,若需要区分时应表述为:“由随机效应 引入的不确定度分量”和“由系统效应引 入的不确定度分量” 7 已知系统误差的估计值时可以对分析 结果进行修正.得到已修正的分析结 果 不能用不确定度对分析结果进行修正,在 已修正分析结果的不确定度中应考虑修正 不完善而引入的不确定度 四、如何提高分析结果的准确度,减少不确定度 分析结果的准确度是指分析结果与真实值之间的一致程度。在定量分析工作中,为了使 分析结果和数据有意义,就要尽量提高分析结果的准确度。因此,定量分析必须对所测的数 据进行归纳、取舍等一系列分析处理(见第十六章);同时,还需根据具体分析任务对准确 度的要求,合理判断和正确表述分析结果的可靠性与精密度以及分析的不确定度。为此,分 析人员应该了解分析过程中产生误差的原因及误差出现的规律,并采取相应的措施减小误 差,使分析结果尽量地接近客观的真实值。 从前面有关误差的讨论中可知,在分析测试过程中,不可避免地存在误差和不确定度。 那么如何尽可能地减小分析误差和分析的不确定度,提高分析结果的准确度呢?下面结合实 际情况简单地予以讨论。 1.选择合适的分析方法 各种分析方法的准确度和灵敏度是不同的,在实际工作中要根据具体情况和要求来选择 分析方法。化学分析法中的重量分析和滴定分析相对于仪器分析而言,准确度高,但灵敏度 低,适用于质量分数高的组分的测定。而仪器分析方法相对而言灵敏度高,准确度低,因此 它适于质量分数低的组分的测定。例如有一试样铁的质量分数为 40.10%,若用重铬酸钾法 滴定铁,其方法的相对误差为 ± 0.2%,则铁的质量分数范围是 40.02%~40.18%。若采用分
开始 说明分析对象 第一步 识别不确定度来源 第二步 将现有数据的不确定度 第三步 来源分组以简化评估 量化各组分量 最化其他分量 将分量转化为标准 编类 计算合成标准不确定度 第四步 复核,如必要,重新评 估较大的分量 结束 计算扩展不确定度 图15-1不确定度的评估过程
5 图 15-1 不确定度的评估过程 开始 说明分析对象 识别不确定度来源 将现有数据的不确定度 来源分组以简化评估 量化各组分量 量化其他分量 将分量转化为标准 偏差 计算合成标准不确定度 复核,如必要,重新评 估较大的分量 结束 计算扩展不确定度 第二步 第一步 第三步 第四步