豌豆杂种F,代性状分离的观察次数与理论次数(n=556) 黄子叶 黄子叶 绿子叶 绿子叶 次数 饱满 皱缩 饱满 皱缩 实际次数(O) 315 101 108 32 理论次数E) 312.75 104.25 104.25 34.75 假设H:F2代的分离符合93:3:1的理论比率 22=315-312.75y+101-104.25+108-104.25432-34.752 =0.470 312.75 104.25 104.25 34.75 df2k-1=4-1=3 x2=0.47<x20.05,3=7.815,p>5%,接受H0。 认为豌豆杂种F,代的分离是符合9:3:3:1的理论比率
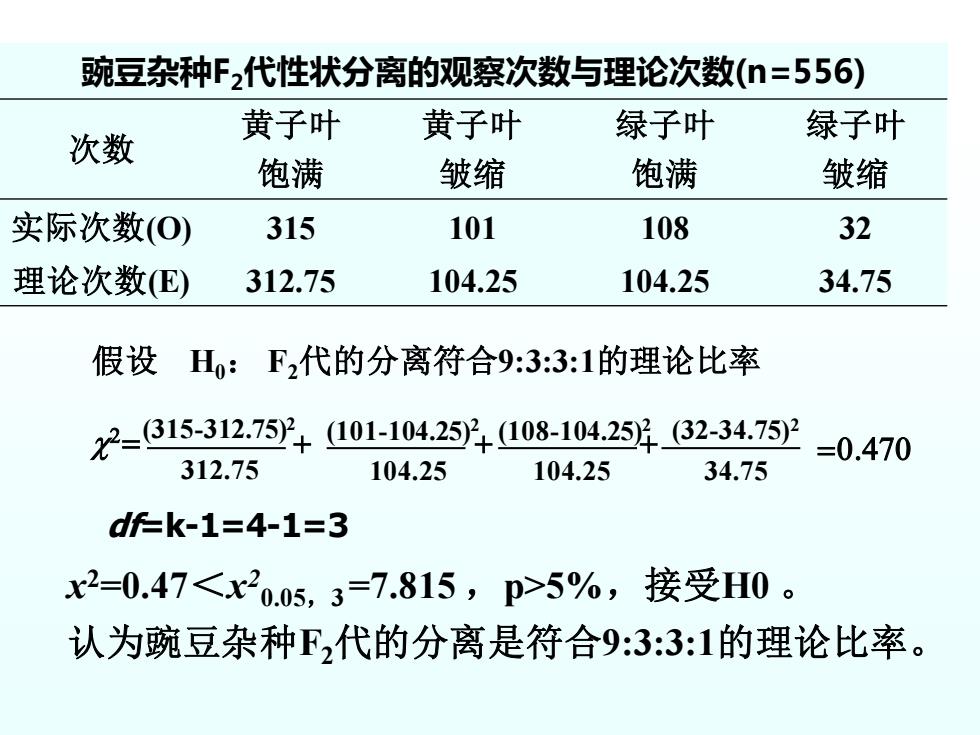
豌豆杂种F2代性状分离的观察次数与理论次数(n=556) 次数 黄子叶 饱满 黄子叶 皱缩 绿子叶 饱满 绿子叶 皱缩 实际次数(O) 315 101 108 32 理论次数(E) 312.75 104.25 104.25 34.75 假设 H0: F2代的分离符合9:3:3:1的理论比率 2= + + + (32-34.75)2 (315-312.75)2 (101-104.25)2 (108-104.25)2 312.75 104.25 104.25 34.75 =0.470 df=k-1=4-1=3 x 2=0.47<x 2 0.05,3=7.815 ,p>5%,接受H0 。 认为豌豆杂种F2代的分离是符合9:3:3:1的理论比率

【例6.2】有一批水稻种子,规定发芽率达80%合格, 即发芽:不发芽=4:1。随机抽200粒做发芽试验,发芽 种子数为150粒。这批水稻种子是否合格? 假设H:合格,即发芽:不发芽=4:1 发-20-E1-052 E 150-16d-0.52+50-40-0.5=2.82 160 40 dk-1=2-1=1,由附表4查出2x2.05,1=3.84。 结论:x2<o.5,1,不能否定H,认为这 批水稻种子是合格的
假设 H0:合格,即发芽:不发芽=4:1 df=k-1=2-1=1,由附表4查出 2 0.05,1 =3.84 。 结论: c 2< 2 0.05,1,不能否定H0,认为这 批水稻种子是合格的。 Oi -Ei -0.5)2 2 = Σ 1 k i = Ei c ( = + =2.82 ( 150-160 -0.5)2 ( 50-40 -0.5)2 160 40 【例6.2 】有一批水稻种子,规定发芽率达80%合格, 即发芽:不发芽=4:1。随机抽200粒做发芽试验,发芽 种子数为150粒。这批水稻种子是否合格?

&6.3独立性测验 独立性测验(independence test)是 测验两个变数之间是相互独立还是彼 此相关的统计方法,是次数资料的一 种相关研究。 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 &6.3 独立性测验 ◼ 独立性测验(independence test)是 测验两个变数之间是相互独立还是彼 此相关的统计方法,是次数资料的一 种相关研究

X2独立性其方法和步骤是: Ho:两个变数相互独立, HA:两个变数彼此相关。 将资料按两向分组排列成r行、c列的相依表(表5.3)。 X2基本公式或变形公式计算x2值 按自由度d(r-1)c-1)查表进行x2测验。 写统计结论
X2独立性其方法和步骤是: H0:两个变数相互独立, HA:两个变数彼此相关。 将资料按两向分组排列成r行、c列的相依表(表5.3)。 按自由度df=(r-1)(c-1)查表进行 2测验。 X2基本公式或变形公式计算x 2值 写统计结论