
解题方法 由初始条件求解振幅和初相位: 设t=0时,振动位移:x=x0 振动速度:v=0 x=Acos(@t+p) xo Acosp v=-@Asin (@t+o) Vo =-OAsin p
解题方法 由初始条件求解振幅和初相位: 设 t = 0时,振动位移:x = x0 振动速度:v = v0 x = Acos(t + ) x0 = Acos v = −Asin (t + ) v0 = −Asin

xo Acos p 0o Asin p ① (n'p+cos) tan o = NX
2 2 0 0 = + v A x x0 = Acos sin 0 − = A v 2 2 2 2 2 2 2 0 0 x + = A (sin + cos ) = A v o o x v tan = −
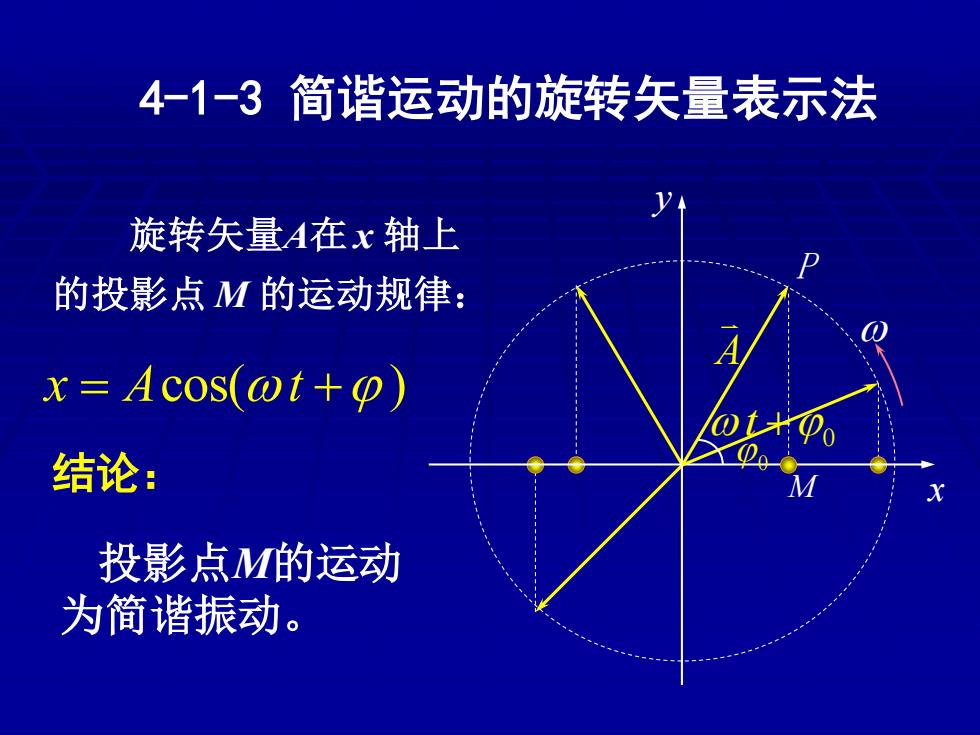
4-1-3简谐运动的旋转矢量表示法 旋转矢量A在x轴上 D 的投影点M的运动规律: x=Acos(@t+o) Po 结论: 投影点M的运动 为简谐振动
4-1-3 简谐运动的旋转矢量表示法 旋转矢量A在 x 轴上 的投影点 M 的运动规律: x = Acos(t + ) 结论: 投影点M的运动 为简谐振动。 y x 0 +0 t A P M
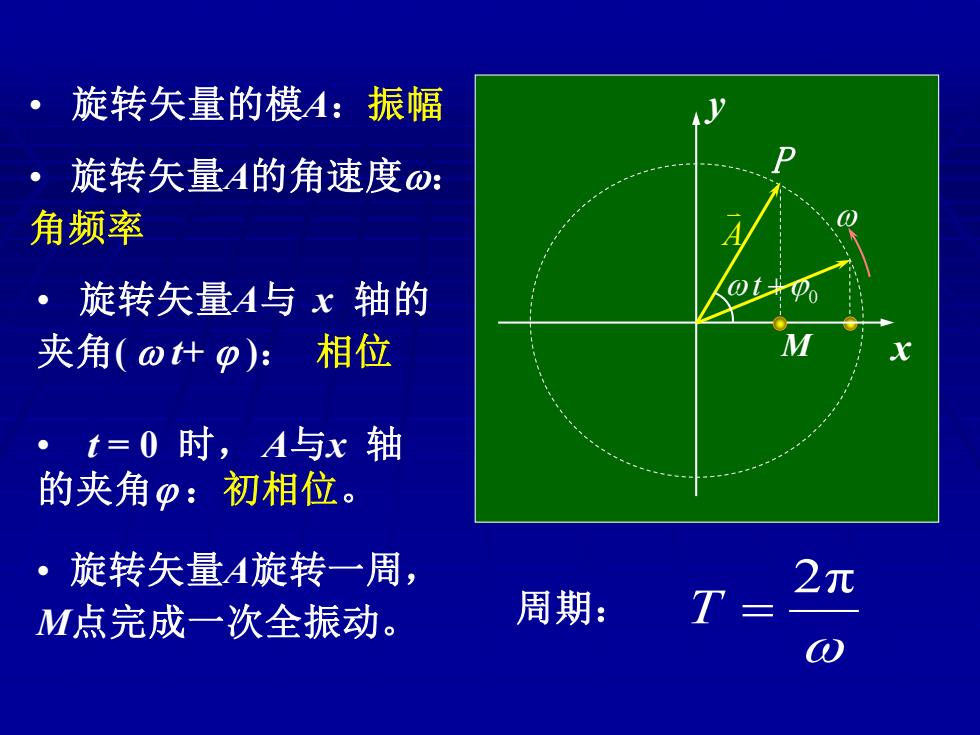
。旋转矢量的模A:振幅 ·旋转矢量A的角速度o: 角频率 ·旋转矢量A与x轴的 夹角(o什p):相位 。t=0时,A与x轴 的夹角p:初相位。 。旋转矢量A旋转一周, T= 2元 M点完成一次全振动。 周期:
y x +0 t A P M • 旋转矢量A旋转一周, M点完成一次全振动。 • 旋转矢量的模A:振幅 • 旋转矢量A的角速度: 角频率 • t = 0 时, A与x 轴 的夹角 :初相位。 • 旋转矢量A与 x 轴的 夹角( t+ ): 相位 2π 周期: T =

例1一质点沿x轴作简谐振动,振幅为12cm,周期为 2s。当t=0时,位移为6cm,且向x轴正方向运动。 求:(1)振动方程;(2)t=0.5s时,质点的位置、速度和加 速度;3)如果在某时刻质点位于x=-6cm,且向x轴负 方向运动,从该位置回到平衡位置所需要的时间。 解:设简谐振动表达式为 x=Acos(@t+p) 2元 已知:A=12cm,T=2s, =π5 T x=0.12cos(ot+p) 初始条件:t=0时,x0=0.06m,0>0
例1 一质点沿x 轴作简谐振动,振幅为12 cm,周期为 2s。当t = 0时, 位移为6 cm,且向x 轴正方向运动。 求:(1)振动方程;(2)t = 0.5 s时,质点的位置、速度和加 速度;(3)如果在某时刻质点位于x = -6 cm,且向 x 轴负 方向运动,从该位置回到平衡位置所需要的时间。 解: 设简谐振动表达式为 已知:A =12 cm , T = 2 s , 1 π 2π − = = s T 初始条件: t = 0 时, x0 = 0.06 m , v0 > 0 x = Acos(t + ) x = 0.12cos(t +)