中国科学技术大学：《应用时间序列分析》课程教学资源（课件讲稿）第三章 平稳时间序列分析

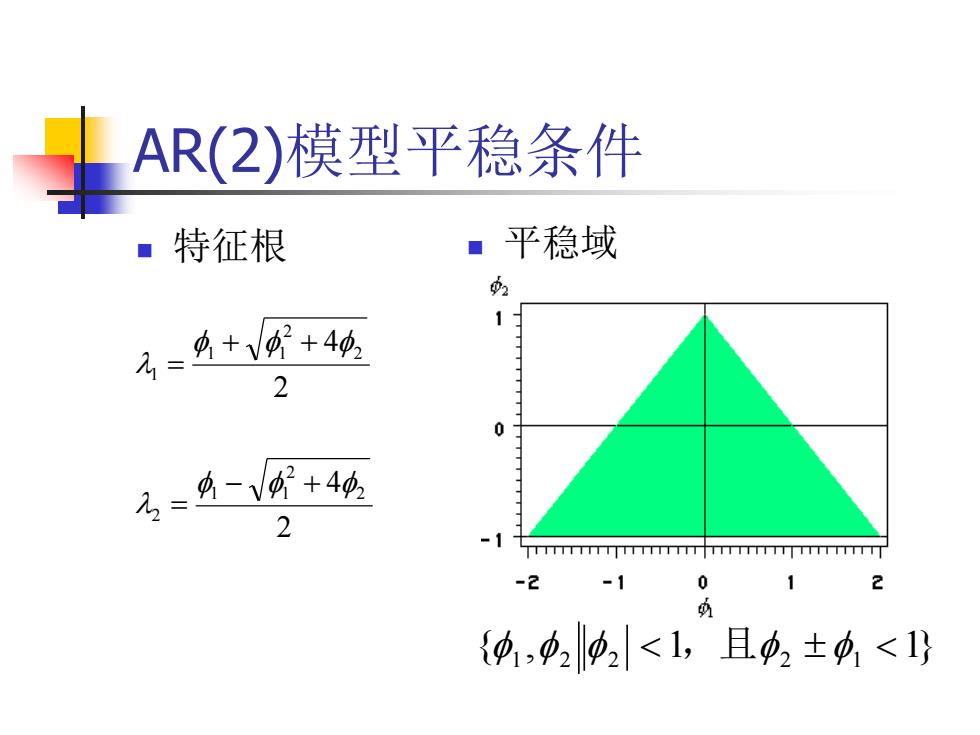
AR(2)模型平稳条件 ■特征根 ■平稳域 名=4+⑧+4顷 2 0 名，=4-+4项 2 TTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT -2 -1 0 1 2 {0,2p2<1,且中2±功<1

AR(2)模型平稳条件  特征根  平稳域 2 4 2 4 2 2 1 1 2 2 2 1 1 1               { , 1 1} 1  2  2  ，且 2 1 

例3.1平稳性判别 模 特征根判别 平稳域判别 论 (1) 21=0.8 p=0.8 平稳 (2) 21=-1.1 p=-1.1 非 平稳 (3) , 4|=0.5,4+4=0.5,4-4=-1.5 平稳 (4) 名1-g 4=0.5,4+4=1.5,42-4=-0.5 非 2 2 平稳

例3.1平稳性判别 0.8 1    0.8 1.1 1     1.1 2 1 1  i   2 1 2  i   2 2 1 2 1            0.5, 0.5, 1.5 2 1 3 1    2 1 3 2    2 2 1 2 1            0.5, 1.5, 0.5 模 型 特征根判别 平稳域判别 结 论 (1) 平稳 (2) 非 平稳 (3) 平稳 (4) 非 平稳

平稳AR模型的统计性质 ■均值 ■方差 ■协方差 ■自相关系数 ■偏自相关系数

平稳AR模型的统计性质  均值  方差  协方差  自相关系数  偏自相关系数

均值 如果AR(p)模型满足平稳性条件，则有 Ex,=E(4+4x-1+…+中pX-p+8i) ■根据平稳序列均值为常数，且{ε，为白噪声序列， 有 Ex,=4,E(E)=0,t∈T ■推导出 功。 4=1---

均值  如果AR(p)模型满足平稳性条件，则有  根据平稳序列均值为常数，且 为白噪声序列， 有  推导出   p       1  0 1 ( ) t 0 1 t 1 p t p t Ex  E   x   x     Ext  ,E( t )  0 ,t T { }t 

Green函数定义 ■AR模型的传递形式 Φ(B)台1-，B i=1i=0 =∑k46△∑G, i0i=1 i=0 ■其中系数{G,j=1,2,}称为Green函数

Green函数定义  AR模型的传递形式  其中系数 {Gj , j 1,2, } 称为Green函数 t j j j j p i t j j i i p i j t j i i p i t i t i t k G k B B k B x                               0 1 0 1 1 0 ( ) ( ) 1