
例3.1:考察如下四个模型的平稳性 (1)x=0.8x-1+8 (2)x,=-1.1x-1+8 (3)x,=x-1-0.5x-2+8 (4)x,=x-1+0.5x-1+8
例3.1:考察如下四个模型的平稳性 1 (1) 0.8 t t t x x 1 (2) 1.1 t t t x x 1 2 (3) 0.5 t t t t x x x t t t t x x x 1 5 1 (4) 0

例3.1平稳序列时序图 ×3 432 432. 1 0 湖 -4 .5 20 4060 80100 20406080100 (1①)x,=0.8x-1+8 (3)x,=x-1-0.5x-2+8
例3.1平稳序列时序图 1 (1) 0.8 t t t x x 1 2 (3) 0.5 t t t t x x x
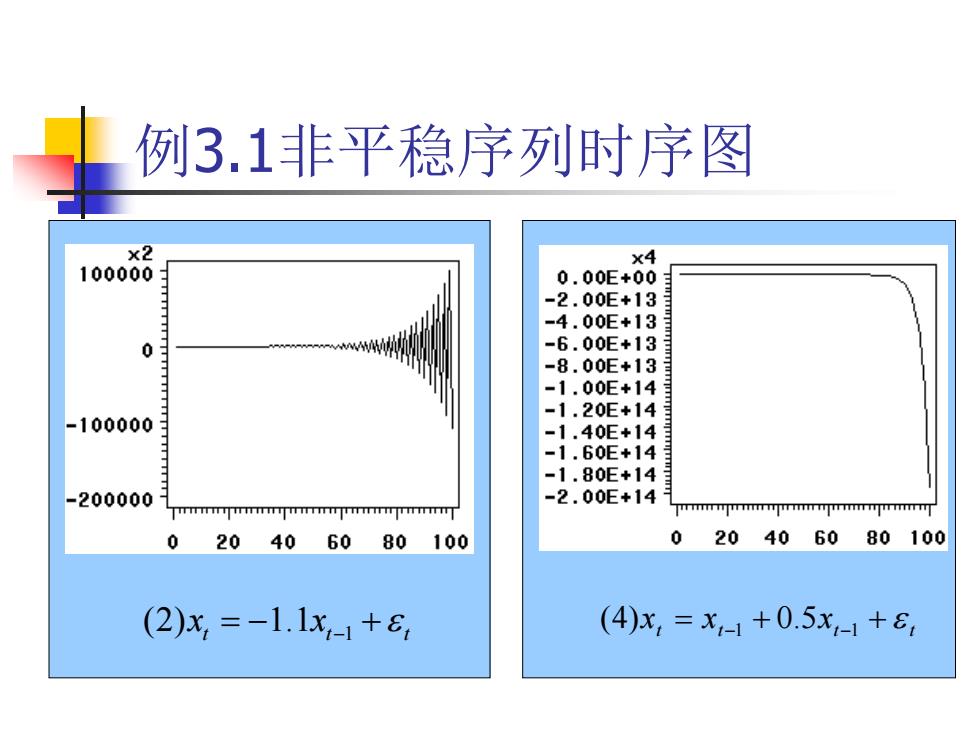
例3.1非平稳序列时序图 x2 x4 100000 0.00E+00 -2.00E+13 -4.00E+13 0 w -6.00E+13 -8.00E+13 -100000 -1.60E+14 -1.80E+14 -200000 -2.00E+14 rmmnjmmmnprrmnpmmnprmnp 0 20406080100 020406080100 (2)x,=-1.1x1+8 (4)x,=x,-1+0.5x-1+8
例3.1非平稳序列时序图 1 (2) 1.1 t t t x x t t t t x x x 1 5 1 (4) 0

AR模型平稳性判别方法 特征根判别 ■AR(p)模型平稳的充要条件是它的p个特征根都在单 位圆内 ·根据特征根和自回归系数多项式的根成倒数的性质, 等价判别条件是该模型的自回归系数多项式的根都 在单位圆外 ■平稳域判别 ·平稳域 {中,中2,…,中,单位根都在单位圆内}
AR模型平稳性判别方法 特征根判别 AR(p)模型平稳的充要条件是它的p个特征根都在单 位圆内 根据特征根和自回归系数多项式的根成倒数的性质, 等价判别条件是该模型的自回归系数多项式的根都 在单位圆外 平稳域判别 平稳域 { , , , } 1 2 p 单位根都在单位圆内

AR(1)模型平稳条件 ■特征根 九=功 ■平稳域 外1
AR(1)模型平稳条件 特征根 平稳域 〈1