
应用统计复习题 线性回归的基本假设和高斯马尔可夫条件 1.解释变量x,x2,…,是非随机变基,观测值x,2,…,z是 常数 2.等方差及不相关的假定条件为 [E(e)=0,i=1,2,…,n l6=g2,=1,2, 0,≠j 这个条件称为高斯-马尔柯夫(Gauss-Markov)条件,简称GM条件。在此条 件下,便可以得到关于回归系数的最小二乘估计及误差项方差。估计的一些重 要性质,如回归系数的最小二乘估计是回归系数的最小方差线性无偏估计等。 3.正态分布的假定条件为 J-N0,a2),i=1,2,…,n 12,…,,相互独立 在此条件下便可得到关于问归系数的最小二乘估计及。2估计的进一步的结果, 如它们分别是回归系数及。2的最小方差无偏估计等,并且可以作回归的显著性 检验及区间估计。 4.通常为了便于数学上的处理,还要求n>p,即样本容量的个数要多于解 释变量的个数。在整个回归分析中,线性回归的统计模型最为重要。一方面是因 推导一元回归的系数最小二乘估计
应⽤统计复习题 线性回归的基本假设和⾼斯⻢尔可夫条件 推导⼀元回归的系数最⼩⼆乘估计
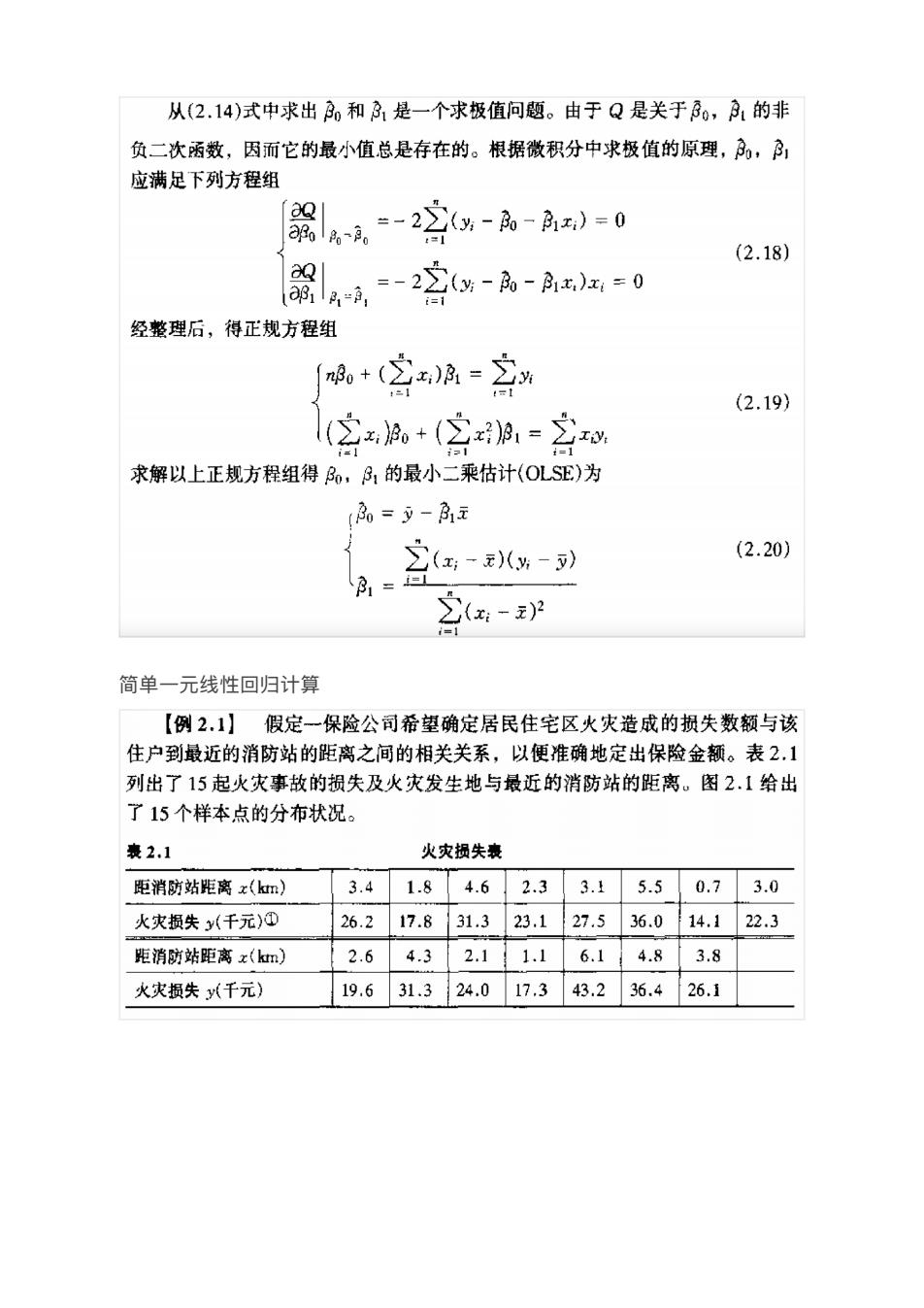
从(2.14)式中求出和31是一个求极值问题。由于Q是关于0,31的非 负二次函数,因而它的最小值总是存在的。根据微积分中求极值的原理,月,序 应满足下列方程组 器4-2%-A-)=0 「aQ (2.18) 器-2-A-Ax话=0 经整理后,得正规方程组 +(空a=立 (2.19) (2x,o+(空a1=2w 求解以上正规方程组得风,房的最小二柔估计(OLSE)为 =y-商 2(x-(%-) (2.20) 之(-P 简单一元线性回归计算 【例2,1】假定一保险公司希望确定居民住宅区火灾造成的损失数额与该 住户到最近的消防站的距离之间的相关关系,以便准确地定出保险金额。表2.1 列出了15起火灾事故的损失及火灾发生地与最近的消防站的距离。图2.1给出 了15个样本点的分布状况 表2.1 火灾损失表 距消防站距离x(m) 3.41.84.62.33.15.50.73.0 火灾损失y(千元)① 26.217.831.323.127.536.014.122.3 距消防站距离x(m) 2.64.32.11.16.14.83.8 火灾损失(千元) 19.631.324.017.343.236.426.1
简单⼀元线性回归计算

利用上述公式就可以具体计算回归方程的参数。下面以例2.1数据为例,建 立火灾损失与住户到最近的消防站的距离之间的回归方程。很据表2.1数据计算 得 %=3.28,9=2=2640 ba=空-(z =196.16-15×(3.28)2=34.784 Ln=空ow-酒 =1470.65-1299.536=171.114 代入(2.23)式得 =-31x=26.413-4.919×3.28=10.279 31=La/L=171.11434.784=4.919 于是回归方程为 y=10.279+4.919x 证明最小二乘估计所得的系数是无偏的 E(A)= x4-元 E(y) j=1 会名归 =王—(角+月)= (2.39) 证得月是月的无偏估计,其中用到∑(x-)=0,∑(x4-x)x= ∑(-)。同理可证A是风的无偏估计,证明过程请读者自己完成。 最小二乘估计系数的方差推导
证明最⼩⼆乘估计所得的系数是⽆偏的 最⼩⼆乘估计系数的⽅差推导

由1,2,…,为相互独立,ar()=2及(2.37)式,得 var(ai)=】 var(片) =1 ()2 var(Bo) = 一元回归的方程显著性检验与区间估计 也就是说自变量x的变化对因变量y并没有影响。由(2.44)式知,A一N (,号)因而当原假设Ho:A=0成立时有 a-No,】 (2.51) 此时,在零附近波动,构造t统计量 t1 A红 (2.52) 其中 =中2"2-加 (2.53) 是。2的无偏估计,称G为回归标准差。 当原假设H,:A=0成立时,(2.52)式构造的:统计量服从自由度为n一2 的t分布。给定显著性水平a,双侧检验的临界值为t,2。当t≥t,2时拒绝原 假设H0R=0,认为A显著不为零,因变量y对自变量x的一元线性回归成 立;当|:<t。2时接受原假设Ho:A=0,认为A为零,因变量y对自变量x的 一元线性回归不成立
⼀元回归的⽅程显著性检验与区间估计

在实际应用中,我们主要关心回归系数房的精度,因而这里只推导,的置 信区间。根银(2.4)式-NA)可得 8山 (2.66) 服从自由度为n-2的t分布。因而 p组-8<4aa-2到=1-。 (2.67) 上式等价于 Pa-是<<a+是I-。 (2.68) 即得A的置信度为1-a的置信区间为 a6是A+a2 (2.69) 画出方差分析表(ANOVA) 表2.3 一元线性回归方整分析表 方差米源工自由度厂平方和 均方 F值 P值 SSR/1 SSR/1 P(F>F值) -2 SE/八m-2) SSE/(n-2) =P值 总和 n-1 sST 证明方差分解式 含·护=多-驴+空(%- (2.55) 其中,之(-?称为总平方和,简记为SST或SB或L·ST表示Sum of Squares for Total。 空位一小称为画自平方和,简记为部或Sa,R表标Rga 之0以~9护称为残差早方和,筒记为签或$a,E表示Em 因而平方和分解式可以简写为 SST=SSR+SSE
画出⽅差分析表(ANOVA) 证明⽅差分解式