
三、时序电路的分类 1.同步时序电路与异步时序电路 同步:存储电路中所有触发器的时钟使用统一的CLK,状态变 化发生在同一时刻 异步:没有统一的CLK,触发器状态的变化有先有后 2. Meal y型和Moore型 Mealy:型: Y=F(X,2) 与X、O有关 Moore型: Y=F(2) 仅取决于电路状态
6 1. 同步时序电路与异步时序电路 同步:存储电路中所有触发器的时钟使用统一的CLK,状态变 化发生在同一时刻 异步:没有统一的CLK,触发器状态的变化有先有后 2. Mealy型和Moore型 Mealy型: Moore型: 三、时序电路的分类 仅取决于电路状态 与 、 有关 ( ) ( , ) Y F Q Y F X Q X Q = =

6.2时序逻辑电路的分析方法 时序逻辑电路可分为: 同步时序电路和异步时序电路。 6.2.1同步时序逻辑电路分析方法 ◆从给定的逻辑图中写出每个触发器的驱动方程。 ◆把得到的驱动方程代入相应触发器的特性方程, 得状态方程,从而得到整个电路的状态方程组。 ◆根据逻辑图写出电路的输出方程。 返回目录
7 时序逻辑电路可分为: 同步时序电路和异步时序电路。 6.2 时序逻辑电路的分析方法 6.2.1 同步时序逻辑电路分析方法 ◆从给定的逻辑图中写出每个触发器的驱动方程。 ◆把得到的驱动方程代入相应触发器的特性方程, 得状态方程,从而得到整个电路的状态方程组。 ◆根据逻辑图写出电路的输出方程
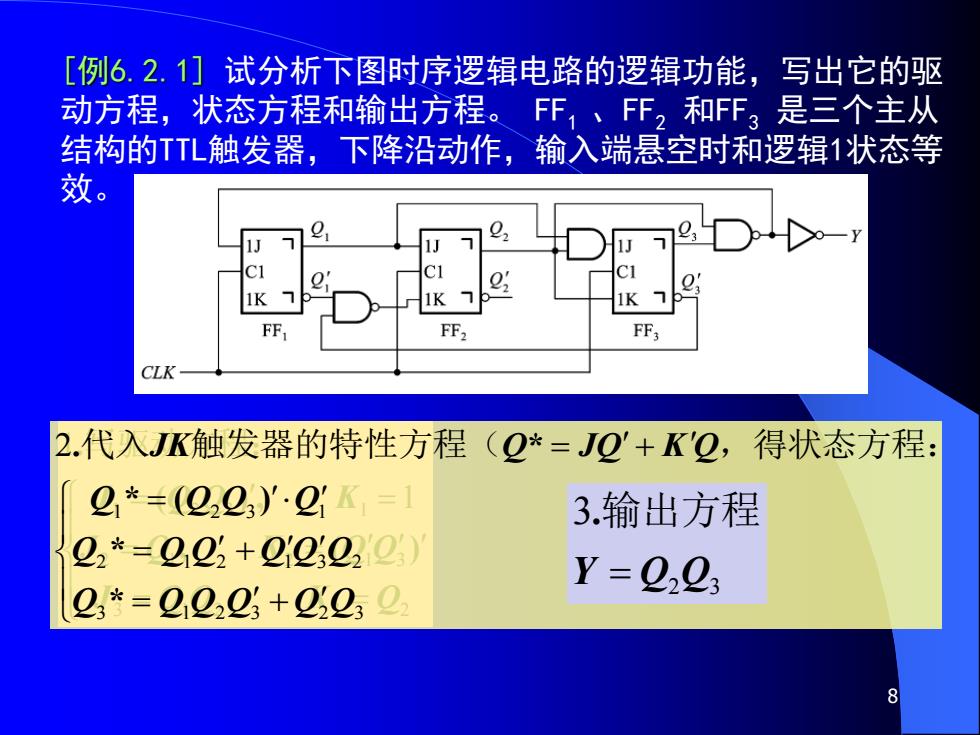
[例6.2.1]试分析下图时序逻辑电路的逻辑功能,写出它的驱 动方程,状态方程和输出方程。FF,、FF2和FF3是三个主从 结构的TTL触发器,下降沿动作,输入端悬空时和逻辑1状态等 效。 1K FF. FF 2.代入JK触发器的特性方程(Q*=JQ'+K'Q,得状态方程: 2*=(2223)'21K,= 3.输出方程 22*=22,+2222 Y=0223 2*=2222+25Q
8 [例6.2.1] 试分析下图时序逻辑电路的逻辑功能,写出它的驱 动方程,状态方程和输出方程。 FF1 、FF2 和FF3 是三个主从 结构的TTL触发器,下降沿动作,输入端悬空时和逻辑1状态等 效。 = = = = = = 3 1 2 3 2 2 1 2 1 3 1 2 3 1 1 1 J Q Q K Q J Q K Q Q J Q Q K , , ( ) ( ) , .写驱动方程: = + = + = = + 3 1 2 3 2 3 2 1 2 1 3 2 1 2 3 1 2 Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q JK Q JQ K Q * * * ( ) .代入 触发器的特性方程( * ,得状态方程: 2 3 3 Y = Q Q .输出方程

6.2.2时序逻辑电路的状态转换表、状态转换 图、状态机流程图和时序图 一、状态转换表 →若将任何一组输入变量及电路初态的取值代入状态方程和输 出方程,即可算出电路的次态和现态下的输出值; →以得到的次态做为新的初态,和这时的输入变量取值一起再 代入状态方程和输出方程进行计算,又得到一组新的次态 和输出值; →如此继续下去,把全部的计算结果列成真值表的形式,就得 到状态转换表
9 6.2.2 时序逻辑电路的状态转换表、状态转换 图、状态机流程图和时序图 一、状态转换表 →若将任何一组输入变量及电路初态的取值代入状态方程和输 出方程,即可算出电路的次态和现态下的输出值; →以得到的次态做为新的初态,和这时的输入变量取值一起再 代入状态方程和输出方程进行计算,又得到一组新的次态 和输出值; →如此继续下去,把全部的计算结果列成真值表的形式,就得 到状态转换表.
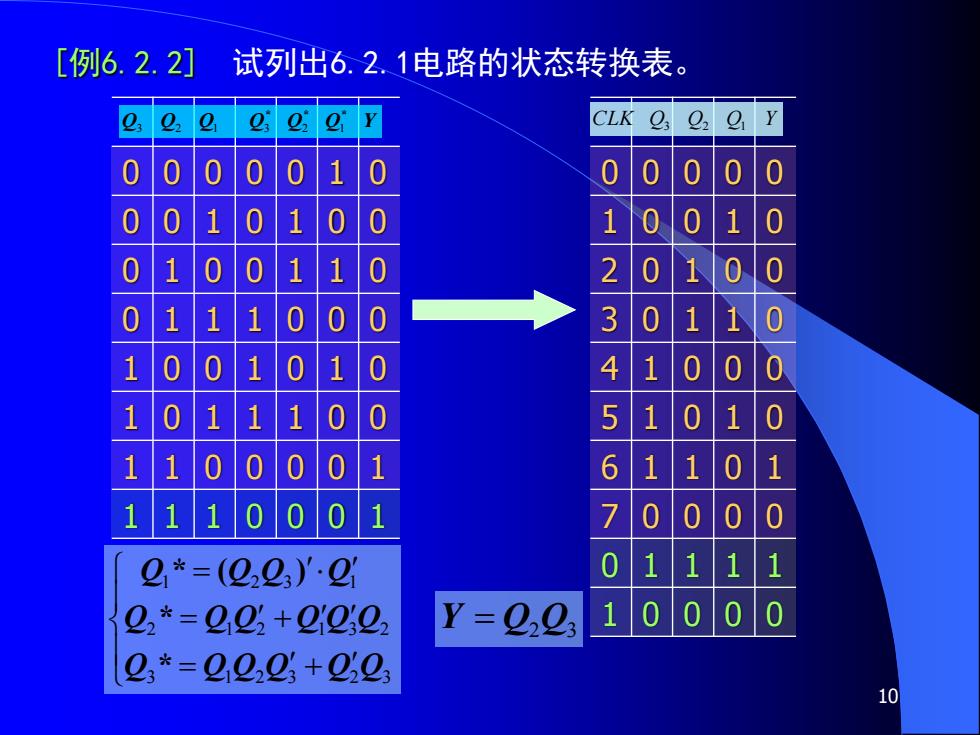
[例6.2.2】试列出6.2.1电路的状态转换表。 e,e,e CLK 00 0 0 010 0 0 0 0 0 00 100 100 1 0 010 01 10 2010 0 01 1 1000 30110 100 1010 4 100 0 10 1100 5 1 0 1100 1 6 1 1110001 7 0 2*=(0223)'·2 Q2*=222+2222 Y=2223 0 Q3*=2222+050 10
10 [例6.2.2] 试列出6.2.1电路的状态转换表。 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 1 1 0 0 1 1 1 0 0 0 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 1 0 0 1 0 2 0 1 0 0 3 0 1 1 0 4 1 0 0 0 5 1 0 1 0 6 1 1 0 1 7 0 0 0 0 0 1 1 1 1 1 0 0 0 0 CLK Q3 Q2 Q1 Y = + = + = 3 1 2 3 2 3 2 1 2 1 3 2 1 2 3 1 Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q * * * ( ) Y = Q2 Q3 Q Q Q Q Q Q Y * * * 3 2 1 3 2 1