
11.4波的能量 波的强度 11.4波的能量波的强度 一.波的能量 设平面简谐波表式为 y(x,t)=Acos@ 质元dm(pdV)的动能和势能 可以证明dEp≡dEk 前页后页目录 1
前页 后页 目录 1 11.4 波的能量 波的强度 一. 波的能量 设平面简谐波表式为 质元dm(dV )的动能和势能 1 2 2 2 2 k d (d ) sin x V A t u E = − dEp dEk ( , ) cos x y x t A t u = − 可以证明 11.4 波的能量 波的强度
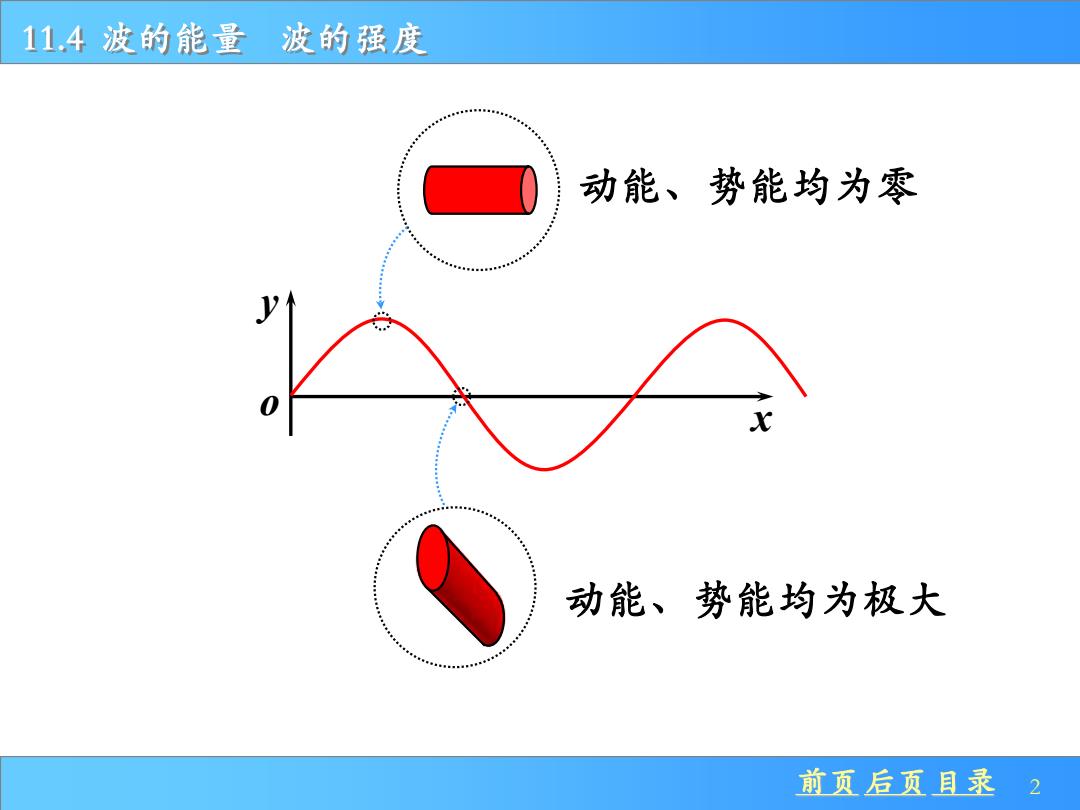
11.4波的能量波的强度 动能、势能均为零 动能、势能均为极大 前页后页目录 2
前页 后页 目录 2 11.4 波的能量 波的强度 y o x 动能、势能均为零 动能、势能均为极大

11.4波的能量波的强度 质元的总机械能 EdE+dv) 2.波的能量密度w 介质中单位体积内的波动能量 w=dE ."sin2@ 平均能量密度w 能量密度在一个周期的平均值 w=wdt=22122 省略推导 前页后页目录 3
前页 后页 目录 3 11.4 波的能量 波的强度 质元的总机械能 dE = + d d Ek p E 2.波的能量密度 能量密度在一个周期的平均值 2 2 2 (d ) sin x V A t u = − 2 2 2 sin x A t u = − 1 2 2 2 = A 介质中单位体积内的波动能量 d d E w V = 0 1 d T w w t T = 平均能量密度 w w 省略推导
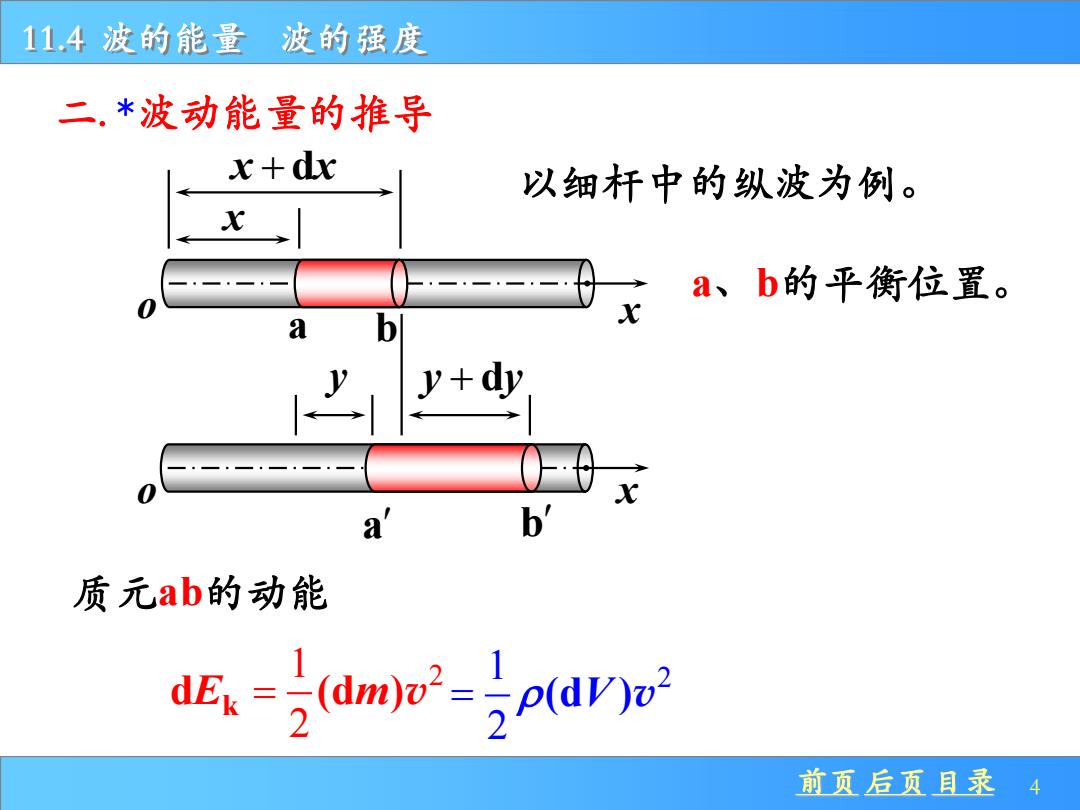
11.4波的能量 波的强度 二.*波动能量的推导 x+dx 以细杆中的纵波为例。 一一 a、b的平衡位置。 a b y+dy a b' 质元ab的动能 dE.-(dm)o-jp(dY)o 前页后页目录 4
前页 后页 目录 4 11.4 波的能量 波的强度 二. *波动能量的推导 以细杆中的纵波为例。 x x x + d o x a b a、b的平衡位置。 o y y y + d a b x 质元ab的动能 1 2 2 = (d ) V v 1 2 2 d (d ) E m k = v

11.4波的能量波的强度 质元ab的振动速度 v---Aosin@ 8t 质元ab的势能dE,=2k(d 由杨氏模量定义和胡克定律 =E f=kdy k=ES S dx dx 前页后页目录 5
前页 后页 目录 5 11.4 波的能量 波的强度 质元ab的振动速度 则 1 2 2 2 2 d (d ) sin k x E V A t u = − 质元ab的势能 由杨氏模量定义和胡克定律 f k y = d y t = v sin x A t u = − − 1 2 2 d (d ) E k y p = d d f y E S x = 1 d k ES x =