
10.4电磁振荡 10.4电磁振荡 电磁振荡 电路中电压和电流的周期性变化。 一LC电路的振荡 LC振荡电路 前页后页目录 1
前页 后页 目录 1 10.4 电磁振荡 电磁振荡 电路中电压和电流的周期性变化。 一.LC电路的振荡 K E C L 1 2 LC 振荡电路 10.4 电磁振荡
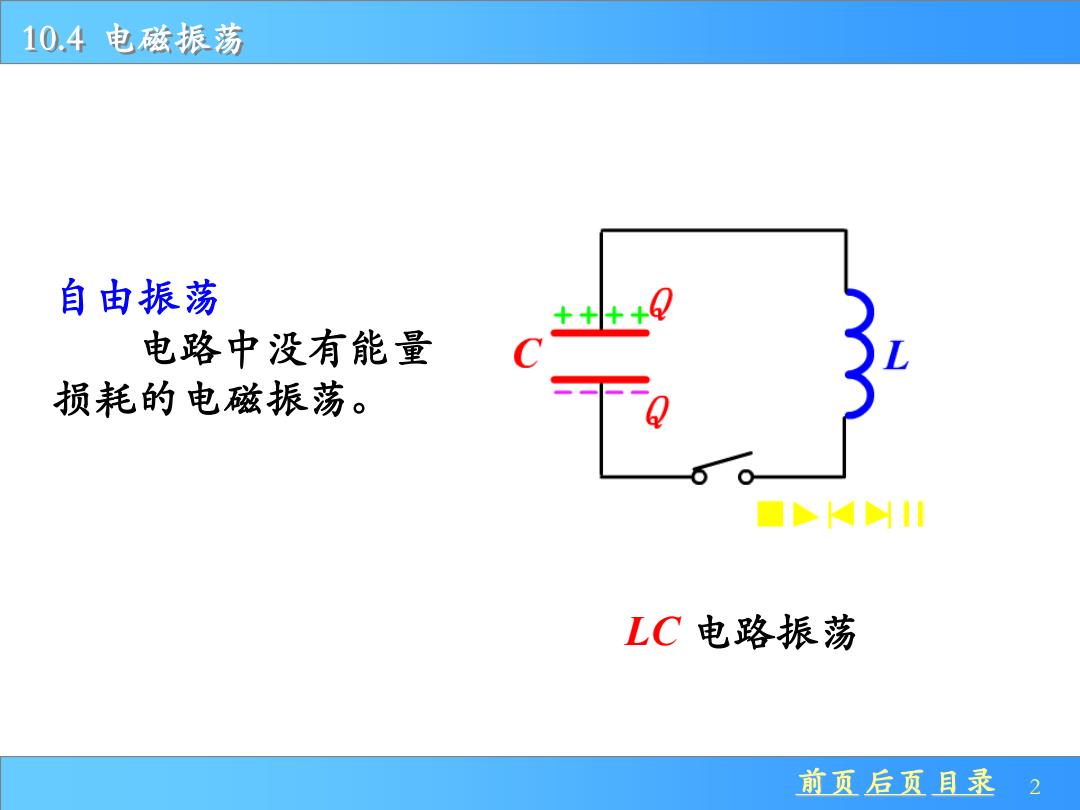
10.4电磁振荡 自由振荡 60 电路中没有能量 损耗的电磁振荡。 Q KNII LC电路振荡 前页后页目录 2
前页 后页 目录 2 10.4 电磁振荡 LC 电路振荡 自由振荡 电路中没有能量 损耗的电磁振荡
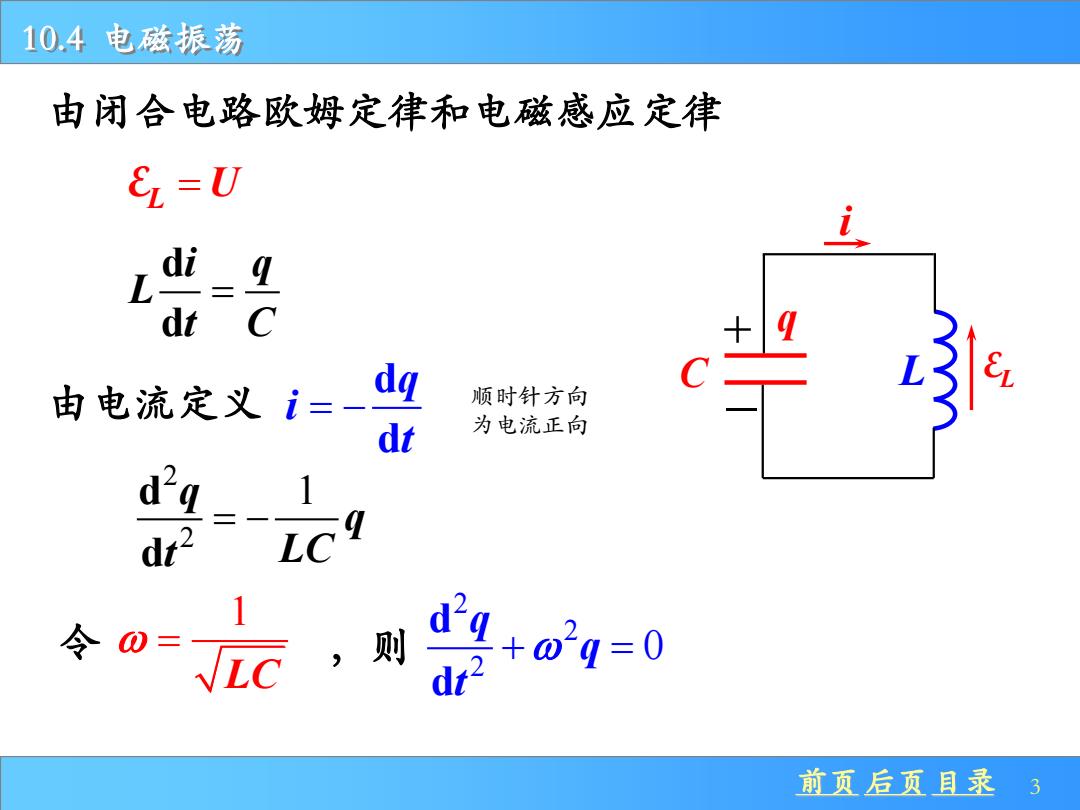
10.4电磁振荡 由闭合电路欧姆定律和电磁感应定律 E=U dt C 由电流定义i= dq 顺时针方向 dt 为电流正向 dq 1 dr2 1 令0= VLC ,则 +0q=0 前页后页目录 3
前页 后页 目录 3 10.4 电磁振荡 C L + q − i LE 由闭合电路欧姆定律和电磁感应定律 EL = U d d i q L t C = 由电流定义 d d q i t = − 顺时针方向 为电流正向 2 2 d 1 d q q t LC = − 令 1 LC = ,则 2 2 2 0 d d q q t + =

10.4电磁振荡 微分方程的解 g=2o cos(@t+o) 20一电量振幅。4一振荡初相。 0一LC回路振荡角频率。 LC回路振荡周期和振荡频率 T=2E=2nLC 0 2πNLC 前页后页目录 4
前页 后页 目录 4 10.4 电磁振荡 微分方程的解 0 0 q Q t = + cos( ) Q0—电量振幅。0 —振荡初相。 —LC 回路振荡角频率。 LC 回路振荡周期和振荡频率 2π T = = 2π LC 1 2π LC =

10.4电磁振荡 电路中的电流 i=d业=-o0sin(ot+m) dt 令l=02,则 i=-1osin(@t+o) =1,6os(at+4+2 前页后页目录5
前页 后页 目录 5 10.4 电磁振荡 电路中的电流 d d q i t = 0 0 = − + Q t sin( ) 令I0=Q0,则 0 0 i I t = − + sin( ) 0 0 2 π = + + I t cos( )