
设有一个循环,A→B为不可逆过程,B→A 为可逆过程,整个循环为不可逆循环。 A 则有 (②9+[区9, <0 R,B→A R R =SA-SB R,B→A B -8Σ别 不可逆循环 A→B 或 asw乞9 21
21 R, A B i B A Q S S T → = − A B I B A Q S T → 或 B A I , i A B Q S S T → − 设有一个循环, 为不可逆过程, 为可逆过程,整个循环为不可逆循环。 A B → B A → I, R, 0 i i A B B A Q Q T T → → + 则有 <
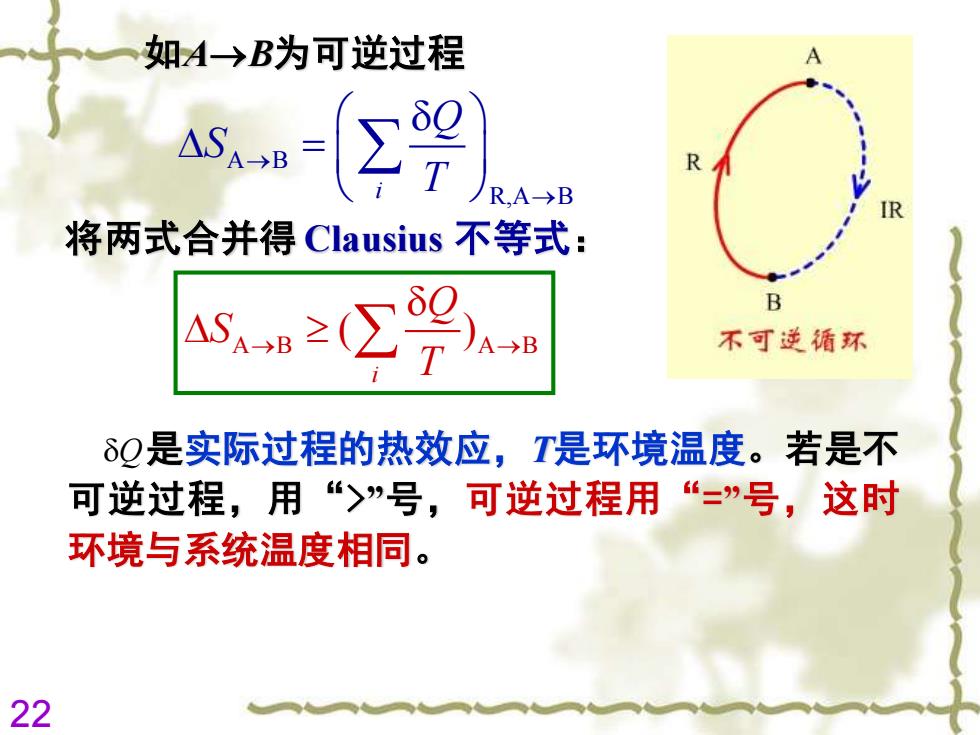
如A→B为可逆过程 A Σ9 R R,A→B 将两式合并得Clausius不等式: A≥∑ B 不可逆循环 δQ是实际过程的热效应,T是环境温度。若是不 可逆过程,用“>”号,可逆过程用“=”号,这时 环境与系统温度相同。 22
22 如A→B为可逆过程 A B i R,A B Q S T → → = A B A B ( ) i Q S T → → 将两式合并得 Clausius 不等式: 是实际过程的热效应,T是环境温度。若是不 可逆过程,用“>”号,可逆过程用“=”号,这时 环境与系统温度相同。 Q
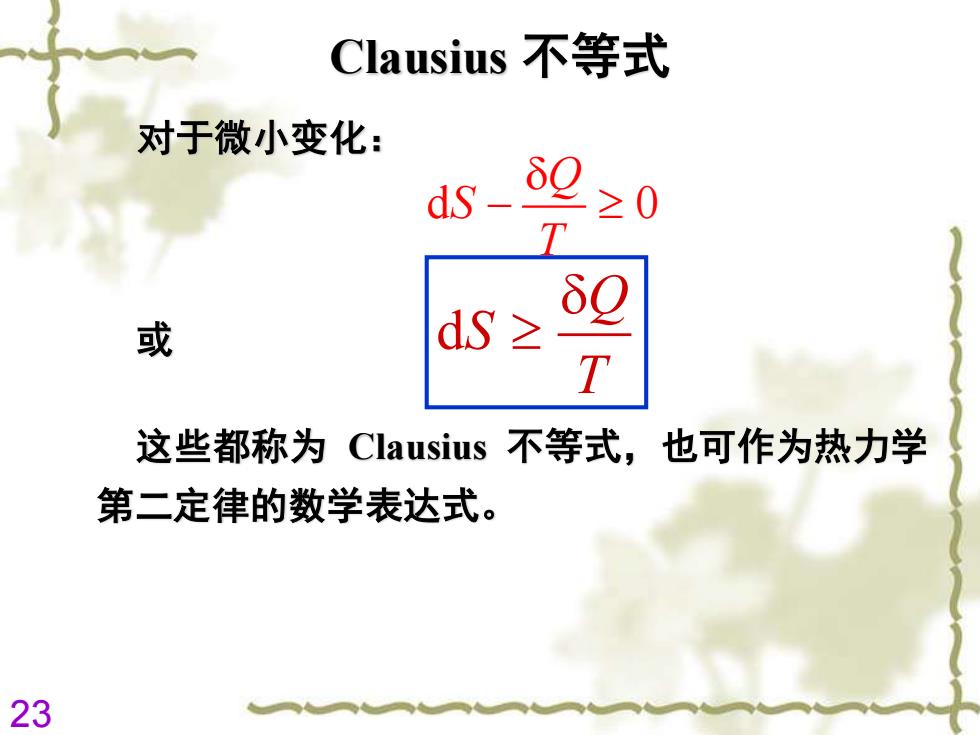
Clausius不等式 对于微小变化: dS δ迴 ≥0 T 或 dS≥ δ9 T 这些都称为Clausius不等式,也可作为热力学 第二定律的数学表达式。 23
23 Clausius 不等式 这些都称为 Clausius 不等式,也可作为热力学 第二定律的数学表达式。 d Q S T 或 d 0 Q S T − 对于微小变化:
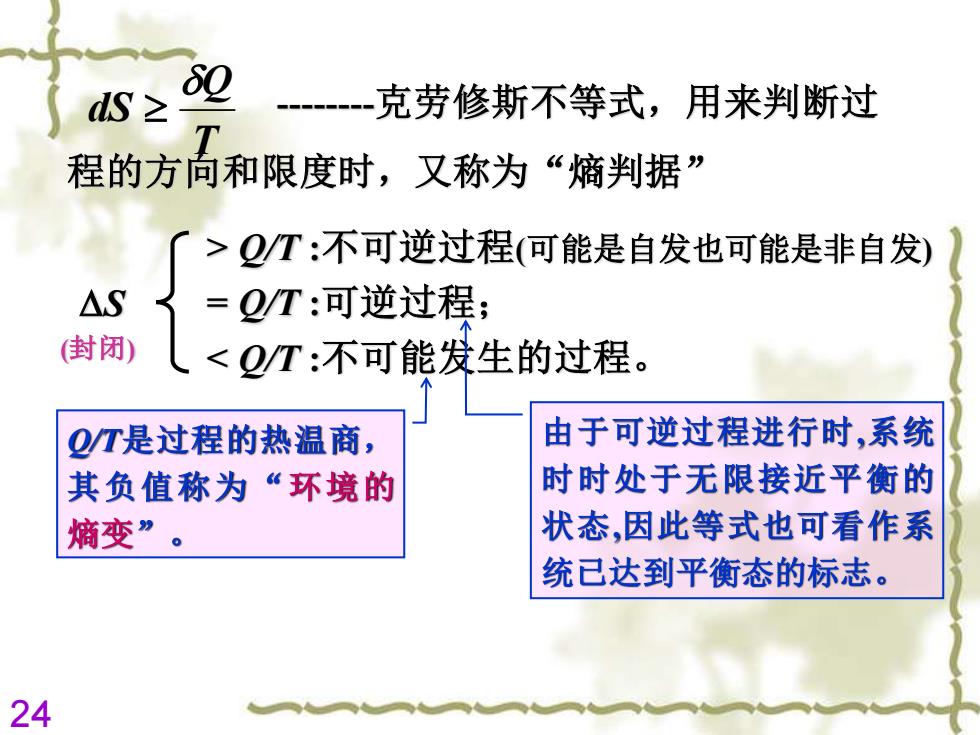
dS≥ 克劳修斯不等式,用来判断过 程的方向和限度时,又称为“熵判据” >QT:不可逆过程(可能是自发也可能是非自发) △S = Q/T:可逆过程; 封闭) <QT:不可能发生的过程。 2T是过程的热温商, 由于可逆过程进行时,系统 其负值称为“环境的 时时处于无限接近平衡的 熵变”。 状态,因此等式也可看作系 统已达到平衡态的标志。 24
24 -克劳修斯不等式,用来判断过 程的方向和限度时,又称为“熵判据” S (封闭) > Q/T :不可逆过程(可能是自发也可能是非自发) = Q/T :可逆过程; < Q/T :不可能发生的过程。 由于可逆过程进行时,系统 时时处于无限接近平衡的 状态,因此等式也可看作系 统已达到平衡态的标志。 Q/T是过程的热温商, 其负值称为“环境的 熵变” 。 T Q dS

熵增加原理 对于绝热系统 δQ=0 所以Clausius不等式为 dS≥0 等号表示绝热可逆过程,不等号表示绝热不可 逆过程。 熵增加原理可表述为:在绝热条件下,趋向于平衡 的过程使系统的熵增加。 或者说:在绝热条件下,不可能发生熵减少的过程 如果是一个隔离系统,环境与系统间既无热的 交换,又无功的交换,则熵增加原理可表述为: 一个隔离系统的熵永不减少 25
25 熵增加原理 对于绝热系统 = Q 0 d 0 S 等号表示绝热可逆过程,不等号表示绝热不可 逆过程。 如果是一个隔离系统,环境与系统间既无热的 交换,又无功的交换,则熵增加原理可表述为: 所以Clausius 不等式为 熵增加原理可表述为:在绝热条件下,趋向于平衡 的过程使系统的熵增加。 或者说:在绝热条件下,不可能发生熵减少的过程 一个隔离系统的熵永不减少