
对非周期信号f来说,我们可看成T>○时的周期函 数,故用同样的办法求得其频谱,但由于T>∞必有 0=平→0,离散的谱线变成了无限密集的连续频谱,对 非周期信号来说,其频谱将是连续的频谱,则傅立叶级数就变 成了傅立叶积分。 f(t)=2元F(o)eodo 其中 F(ω)=nf(t)ecdt 把由f确定的F(o)的变缓称为傅氏正变换(简称傅氏变 换),记为 F(0)=Ff(t)} 相反的由F(o)确定f(t)的变换称为傅氏反变换,并记为 f(t)=F-1{F(o)} f(t)→F(o)
对非周期信号f(t)来说,我们可看成 T → 时的周期函 数, 故用同样的办法求得其频谱,但由于 必有 ,离散的谱线变成了无限密集的连续频谱,对 非周期信号来说,其频谱将是连续的频谱,则傅立叶级数就变 成了傅立叶积分。 T → 0 = 2 T → f t F e d j t − ( ) = ( ) 2 1 其中 F f t e dt j t − − = ( ) ( ) 2 1 把由 f(t) 确定的 F () 的变缓称为傅氏正变换(简称傅氏变 换),记为 F () =F { f(t)} 相反的由F()确定f(t)的变换称为傅氏反变换,并记为 f(t)= F -1{ F()} f(t) F()

频谱函数F(o)一般是一个复数,可记作 F(@)-F(@ei() 其中F(⊙)是F(o)的模,它表示信号中各频率分量的相对大 小;p(@)是F(⊙)的幅角部分,它表示信号中各频率分量的 相位关系。习惯上也把F(D)~o与p(@)~o曲线分别称 为振幅频谱图和相位频谱图。一般而言,若信号f(t)满足绝对 可积条件,即满足 lf(t)dr∞ 则它的傅氏变换一定存在。不过有些信号尽管不能瞒住这 个条件,它们的傅氏变换也存在,因此,绝对可积进近时腐蚀 变化存在的充分条件,而不是必要条件。 例1-2试求图1-7(a)中所示的矩形脉冲的傅氏变换,并画 出它的谱图
频谱函数 F ()一般是一个复数,可记作 ( ) ( ) ( ) j F = F e 其中 是 F ()的模,它表示信号中各频率分量的相对大 小;()是 的幅角部分,它表示信号中各频率分量的 相位关系。习惯上也把 ~ 与 () ~ 曲线分别称 为振幅频谱图和相位频谱图。一般而言,若信号f(t)满足绝对 可积条件,即满足 F() F() F() − f (t) dt 则它的傅氏变换一定存在。不过有些信号尽管不能瞒住这 个条件,它们的傅氏变换也存在,因此,绝对可积进近时腐蚀 变化存在的充分条件,而不是必要条件。 例1−2 试求图1−7(a)中所示的矩形脉冲的傅氏变换,并画 出它的谱图

r){日 -x/2<t〈x/2 利用式(1-13),可求得f)的傅氏变换为 F()-f(t)e-idi-Ae-a dt (e5.5〕4r02 -A5a() 由于F(o)在这里是实函数,所以可以用F(o)曲线同时表示 振幅频谱和相位频谱,如图1-7(b)所示
= 0 ( ) A f t − / 2t / 2 利用式(1-13),可求得f(t)的傅氏变换为 = = − = = = − − − − − 2 / 2 sin( /) ( ) ( ) 2 2 2 2 A Sa e e A j A F f t e dt Ae dt j j T T j t j t 由于F ()在这里是实函数,所以可以用F ()曲线同时表示 振幅频谱和相位频谱,如图1-7(b)所示
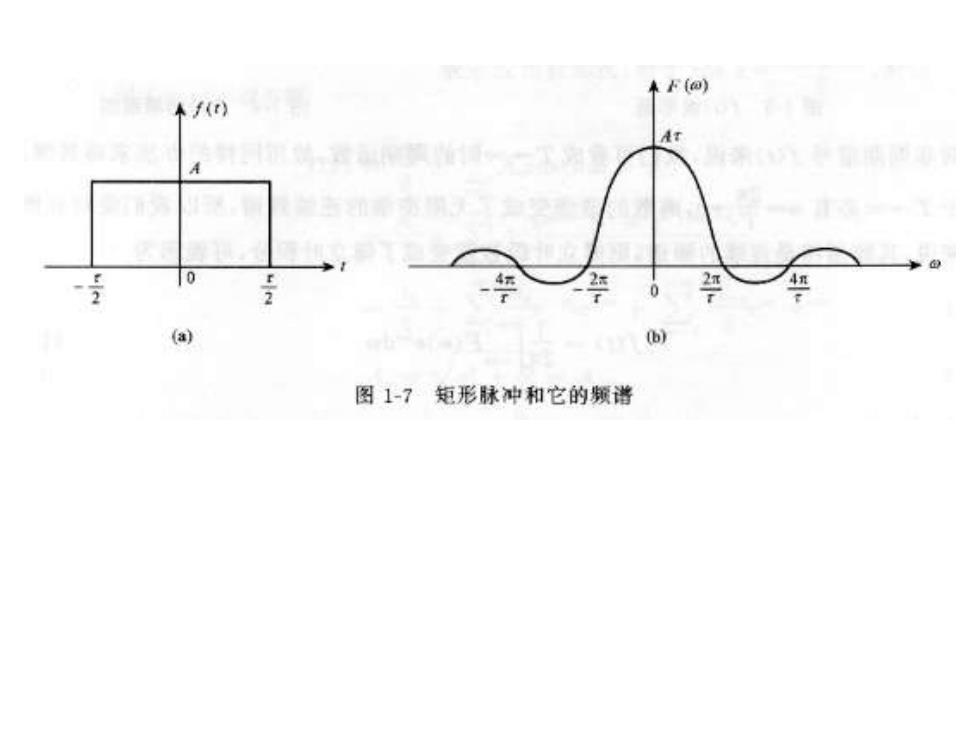
本F@) 本f() A 2 (a) b 图1-7矩形脉冲和它的频谐

第二节 系统响应及分析 一、冲击函数 1、单位冲激信号 单位冲击信号就是时域内的单位冲激函数,它的定义为 -)-{0 t to 其它t 并且有 (t-to)dt =1 抽样性 f(t)δ(t)dt=f(0) f()(t-to)dt =f(to) F[δ(t)]=1
第二节 系统响应及分析 一、冲击函数 1、单位冲激信号 单位冲击信号就是时域内的单位冲激函数,它的定义为 = − = t t t t t 0 其它 ( ) 0 0 并且有 ( − 0 ) =1 − t t dt 抽样性 f (t) (t)dt = f (0) − ( ) ( ) ( ) 0 0 f t t −t dt = f t − F (t)=1