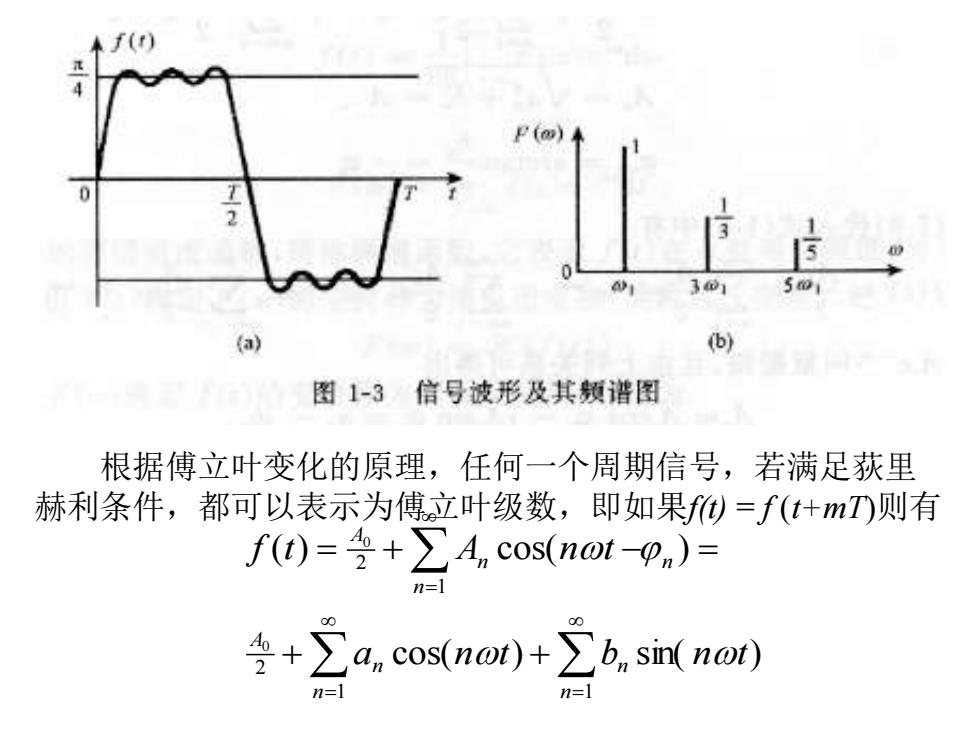
f() P (o) 3⊙ 501 (a)】 (b) 图1-3信号波形及其频谱图 根据傅立叶变化的原理,任何一个周期信号,若满足荻里 赫利条件,都可以表示为傅立叶级数,即如果f=f(t+mT)则有 f(t))=+∑4 cos(not-pn)= n=l ÷+∑a,cos(nor)+2b,sin(not0) n= n=1
根据傅立叶变化的原理,任何一个周期信号,若满足荻里 赫利条件,都可以表示为傅立叶级数,即如果f(t) = f (t+mT)则有 cos( ) sin( ) ( ) cos( ) 1 1 2 1 2 0 0 = = = + + = + − = n n n n A n n n A a n t b n t f t A n t

这里0=严称基波角频率,其中的系数可由下式求得 4-0a (cos(net)de 6=4,sm8,=4=子0saa 并且可知若f为奇函数,则a,=0,若f()为偶函数,则 bn=0。 例如,f如图1-4所示, 求其频谱。 图1-4f)波形图
这里 T 称基波角频率,其中的系数可由下式求得 2 = + = t T t f t dt T A 1 1 ( ) 2 0 + = = = t T t n n n f t n t dt T a A A 1 1 ( ) cos( ) 2 cos 0 + = = = t T t n n n f t n t dt T b A A 1 1 ( )sin( ) 2 sin 0 并且可知若f (t)为奇函数,则an=0,若f (t) 为偶函数,则 bn=0 。 例如,f(t) 如图1-4所示, 求其频谱

为了计算方便,常将傅立叶级数表示成指数形式。 co(mm-) ne-) n= A 2 n=] 2 2 +eme+立2pea 2 上式中 An=Va+b好=Am b P_arctan a
为了计算方便,常将傅立叶级数表示成指数形式。 n jn t j n jn t j n j n t n j n t e e A e e A A e e A A A n t A f t n n n n n n n n n − − − − − − =− − = = = = + + + = + = + − 1 1 0 1 0 1 0 2 2 2 2 2 cos( ) 2 ( ) ( ) ( ) 上式中 n n n n n n n n a b A a b A = = − = + = − − arctan 2 2

f-受+立是eme+2子ee 1三-OO 这里定义An=A,e叫复振幅,且由上列关系可得出 An=An cos pn-jA sin pn=an-jbn 这样函数f可表示 系数A可用下式表示 A-子J臣f(e)emd
j j n t n n j j n t n j j n t n n n e e A e e A e e A A f t n n n − − − − =− − − =− − = = = + + 2 2 2 2 ( ) 1 1 0 这里定义 叫复振幅,且由上列关系可得出 n j n n A A e − = n n n n n n n A = A cos − j A sin = a − j b 这样函数 f(t) 可表示 j n t n f t Ane − =− • = 2 1 ( ) 系数 可用下式表示 • A − − • = 2 2 ( ) 2 T T f t e dt T A j nt

例1-1 设函数f)波形如图1-5所示,求该信号的频谱。 A=2∫f)emat= ∫e not 2 e jugt-ejngt 4 Sin 2 T -ino T no 27 sin n 2 T not sa("g) 2 式中Sa(x)称为抽样函数,作出 该函数的频谱如图1-6所示。 2 4 图1-6f(1)的频谱图
例1-1 设函数 f(t) 波形如图1-5所示,求该信号的频谱。 = = = − − = = = − − − − • − 2 2 sin 2 2 sin 2 4 2 ( ) 2 2 2 2 2 2 2 2 2 n Sa T T n n j n T e e T e dt T f t e dt T A n n n n jn t jn t j j T T 式中 Sa(x) 称为抽样函数,作出 该函数的频谱如图1-6所示