
Content Continuous random variables and pDEs Cumulative Distribution Functions Normal Random Variables Joint PDFs of Multiple Random Variables Conditioning The Continuous Bayes'Rule
Content ◼ Continuous Random Variables and PDFs ◼ Cumulative Distribution Functions ◼ Normal Random Variables ◼ Joint PDFs of Multiple Random Variables ◼ Conditioning ◼ The Continuous Bayes’ Rule

Cumulative distribution Function The cumulative distribution function,or CDF, of a random variable X is Fx(x)=P(X≤X) ∑k≤xpx(k), discrete fxy)dy. continuous The CDF Fx(x)“accumulates”probability“up to”the value x
Cumulative Distribution Function ◼ The cumulative distribution function, or CDF, of a random variable 𝑋 is 𝐹𝑋 𝑥 = 𝑃 𝑋 ≤ 𝑥 = ൝ σ𝑘≤𝑥 𝑝𝑋 𝑘 , discrete ∞− 𝑥 𝑓𝑋 𝑦 𝑑𝑦 , continuous ◼ The CDF 𝐹𝑋 𝑥 “accumulates” probability “up to” the value 𝑥

CDF for discrete case ◆PMF PX(x) CDF Fx(z) 1 Px(2) 0十 1234 PMF Px() CDF Fx() 1 0 01
CDF for discrete case
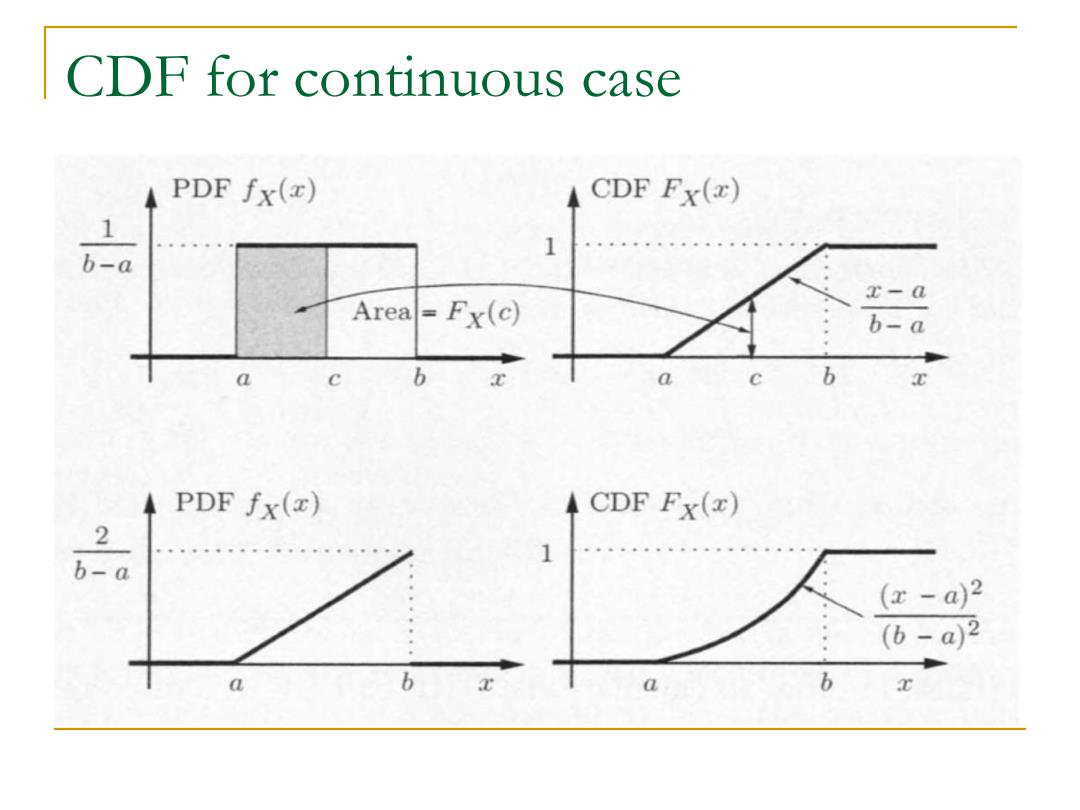
CDF for continuous case PDF fx() CDF Fx(z) 1 1 b-a x-a Area=Fx(c) b-a a b a b PDF fx(z) CDF Fx(z) 2 1 b-a (x-a)2 (b-a)2 a b a b 2
CDF for continuous case

Properties Fx is monotonically increasing: ifx≤y,then Fx(x)≤Fx(y): lim Fx(x)=0,lim Fx(x)=1 X→一00 X→十00 If X is discrete,Fx is piecewise constant. If X is continuous,Fx is continuous and Fx(x)=fx(t)dt, f斥()= 0
Properties ◼ 𝐹𝑋 is monotonically increasing: if 𝑥 ≤ 𝑦, then 𝐹𝑋(𝑥) ≤ 𝐹𝑋(𝑦). ◼ lim 𝑥→−∞ 𝐹𝑋(𝑥) = 0, lim 𝑥→+∞ 𝐹𝑋(𝑥) = 1 ◼ If 𝑋 is discrete, 𝐹𝑋 is piecewise constant. ◼ If 𝑋 is continuous, 𝐹𝑋 is continuous and 𝐹𝑋 𝑥 = න −∞ 𝑥 𝑓𝑋 𝑡 𝑑𝑡, 𝑓𝑋 𝑥 = 𝑑𝐹𝑋 𝑑𝑥 𝑥