
Example:maximum of several random variables Take a test three times with score in {1,..,10} The final score is the maximum of the scores X max(X1,X2,X3) Each Xi takes values {1,..,10}eually likely, and different Xi's are independent. The CDF of the final score X is ·Fx(k)=P(X≤k) =P(X1≤k)P(X2≤k)P(X3≤k) =(k/10)3
Example: maximum of several random variables ◼ Take a test three times with score in {1, . . , 10} ◼ The final score is the maximum of the scores 𝑋 = max(𝑋1,𝑋2, 𝑋3) ◼ Each 𝑋𝑖 takes values {1, . . , 10} eually likely, and different 𝑋𝑖 ’s are independent. ◼ The CDF of the final score 𝑋 is ◼ 𝐹𝑋 𝑘 = 𝑃 𝑋 ≤ 𝑘 = 𝑃 𝑋1 ≤ 𝑘 𝑃 𝑋2 ≤ 𝑘 𝑃 𝑋3 ≤ 𝑘 = (𝑘/10) 3

Example:maximum of several random variables Take a test three times with score in {1,..,10} The final score is the maximum of the scores X=max(X1,X2,X3) Each X;takes values {1,..,10}eually likely, and different Xi's are independent. The PDF of the final score X is 1P=F()-k-)=()-(合)
Example: maximum of several random variables ◼ Take a test three times with score in {1, . . , 10} ◼ The final score is the maximum of the scores 𝑋 = max(𝑋1,𝑋2, 𝑋3) ◼ Each 𝑋𝑖 takes values {1, . . , 10} eually likely, and different 𝑋𝑖 ’s are independent. ◼ The PDF of the final score 𝑋 is ◼ 𝑃𝑋 𝑘 = 𝐹𝑋 𝑘 − 𝐹𝑋 𝑘 − 1 = 𝑘 10 3 − 𝑘−1 10 3
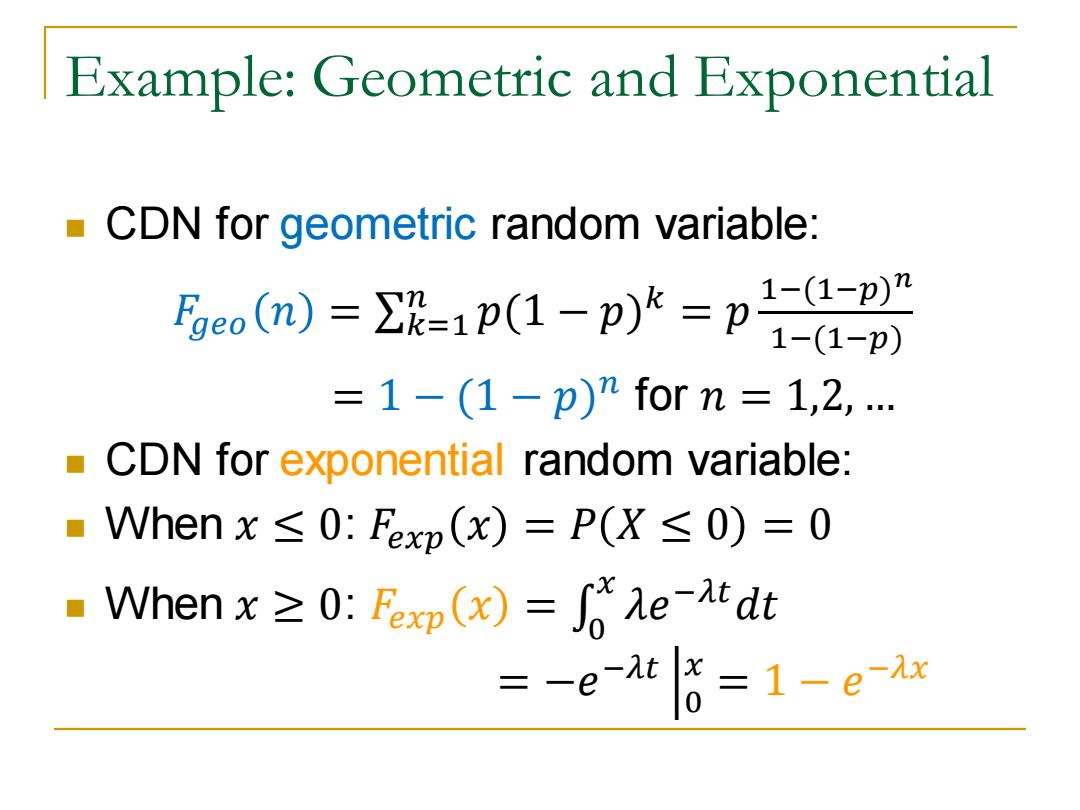
Example:Geometric and Exponential CDN for geometric random variable: e(m0)=2设=1p(1-p)=p1 1-(1-p) =1-(1-p)for n=1,2, CDN for exponential random variable: When x≤0:Fexp(x)=P(X≤0)=0 ■When x≥0:Eem(x)=J0ae-tdt =-e-t 8=1-e-ix
Example: Geometric and Exponential ◼ CDN for geometric random variable: 𝐹𝑔𝑒𝑜 𝑛 = σ𝑘=1 𝑛 𝑝(1 − 𝑝) 𝑘 = 𝑝 1−(1−𝑝) 𝑛 1−(1−𝑝) = 1 − (1 − 𝑝) 𝑛 for 𝑛 = 1,2, … ◼ CDN for exponential random variable: ◼ When 𝑥 ≤ 0: 𝐹𝑒𝑥𝑝 𝑥 = 𝑃 𝑋 ≤ 0 = 0 ◼ When 𝑥 ≥ 0: 𝐹𝑒𝑥𝑝 𝑥 = 0 𝑥 𝜆𝑒 −𝜆𝑡𝑑𝑡 = −𝑒 −𝜆𝑡 ቚ 𝑥 0 = 1 − 𝑒 −𝜆𝑥
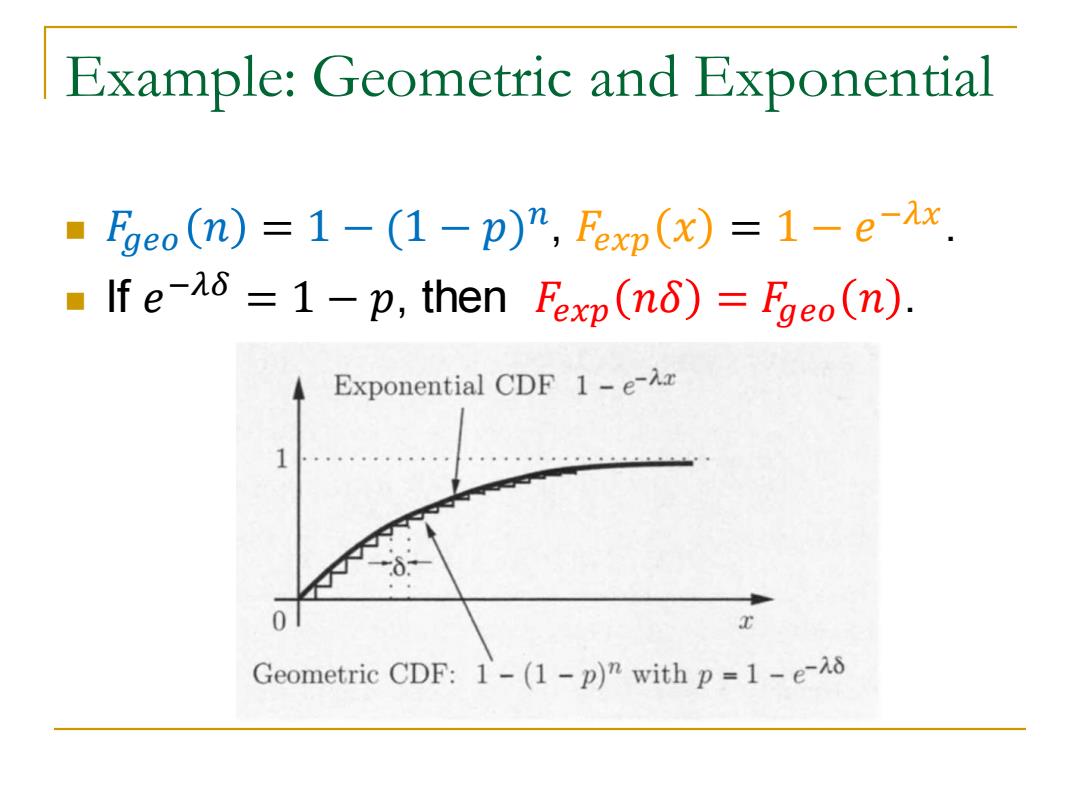
Example:Geometric and Exponential Fgeo(n)=1-(1-p)n,Fexp(x)=1-e-Ax. If e-46 =1-p,then Fexp(n8)=Fgeo(n). Exponential CDF 1-e-Ax Geometric CDF:1-(1-p)n with p=1-e-48
Example: Geometric and Exponential ◼ 𝐹𝑔𝑒𝑜 𝑛 = 1 − (1 − 𝑝) 𝑛 , 𝐹𝑒𝑥𝑝 𝑥 = 1 − 𝑒 −𝜆𝑥 . ◼ If 𝑒 −𝜆𝛿 = 1 − 𝑝, then 𝐹𝑒𝑥𝑝 𝑛𝛿 = 𝐹𝑔𝑒𝑜 𝑛

Content Continuous random variables and pDEs Cumulative Distribution Functions Normal Random variables Joint PDFs of Multiple Random Variables Conditioning The Continuous Bayes'Rule
Content ◼ Continuous Random Variables and PDFs ◼ Cumulative Distribution Functions ◼ Normal Random Variables ◼ Joint PDFs of Multiple Random Variables ◼ Conditioning ◼ The Continuous Bayes’ Rule