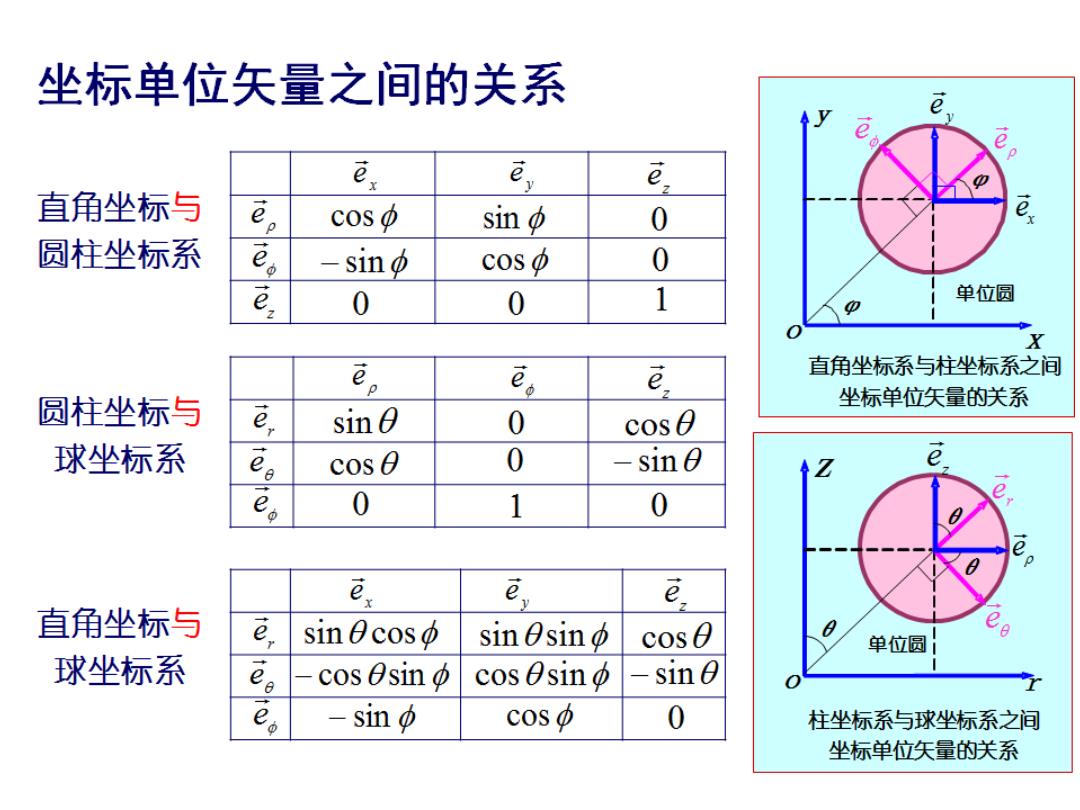
坐标单位矢量之间的关系 e e e e 直角坐标与 e cos中 sin o 0 圆柱坐标系 Sin中 coS中 0 0 0 1 单位圆 X e。 E。 e 直角坐标系与柱坐标系之间 圆柱坐标与 坐标单位矢量的关系 e sin0 0 cos 0 球坐标系 08 cos 0 0 一 sin0 e 0 1 0 e E e 直角坐标与 e e sin 0 coso sin Osino cos0 单位圆引 球坐标系 08 cos esin cos0sin中 sin 0 -sin c0S中 0 柱坐标系与球坐标系之间 坐标单位矢量的关系

二、算子7 >V算子(Del)与微分形式的Maxwell方程密切 相关。在曲线坐标中,算子定义为 (1-1) 其中9,92,93分别是坐标轴91,92,93的单位 矢。H1,H2,H为坐标系的拉梅系数
二、 算子∇

>函数f的梯度、失量函数∫=9+592+f9 的散度和旋度定义如下: 成器元器+元哥 。 Vf=4H104 (1-2) 了产7保风0+ (H,H,f)+aa (H,H2f】1-3) Hig H292 Hds V×f= 6 1-4 H,H,Hs a 6q2 6q3 H H3f 例:已知矢量函数是无旋的,确定系数 F=a,(3y-cz)+a,(czx-2z)-a.(c3y+z)
例:已知矢量函数是无旋的,确定系数 1 2 3 (3 ) ( 2 ) ( ) F a y c z a c x z a c y z = − + − − + x y z
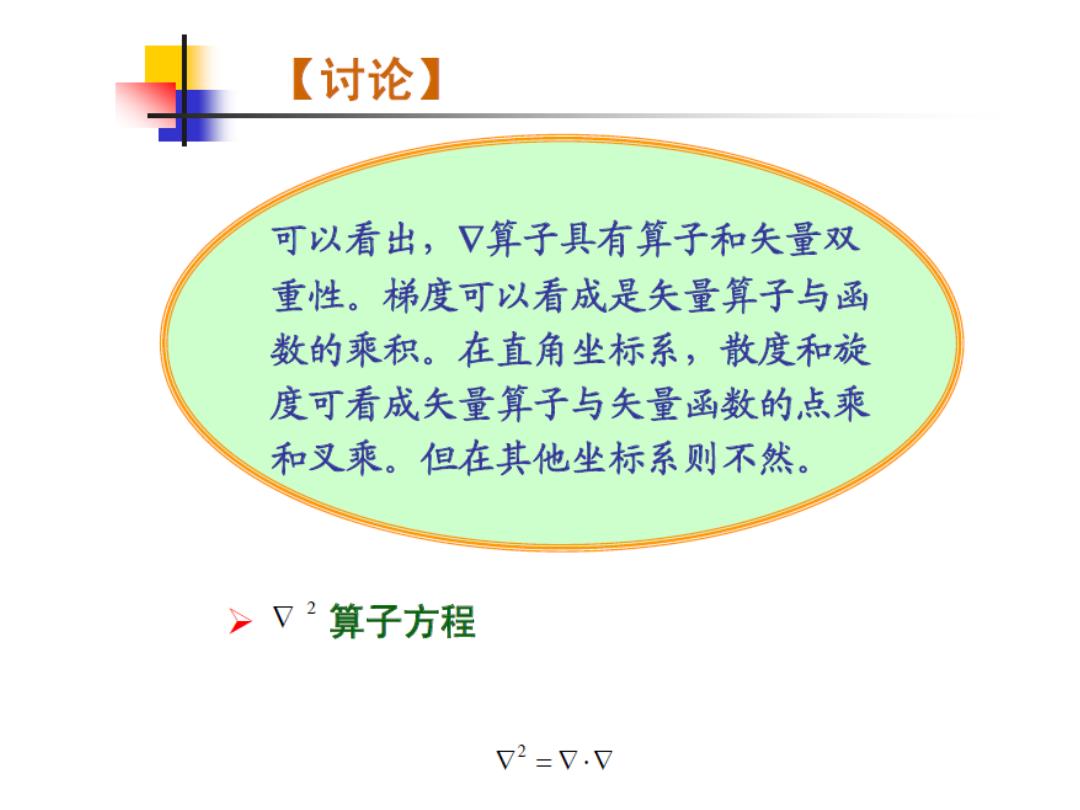
【讨论】 可以看出,又算子具有算子和失量双 重性。梯度可以看成是矢量算子与函 数的乘积。在直角坐标系,散度和旋 度可看成失量算子与失量函数的,点乘 和叉乘。但在其他坐标系则不然。 >V2算子方程 72=7.7

V×VU≡0 标量场梯度的旋度恒等于零。 V.(V×①=0 矢量场的旋度之散度恒等于零。 总结出V算子的运算原则: (1)利用矢量公式; (2)V算子始终在作用函数的左边,非作用函 数的右边
U 0 标量场梯度的旋度恒等于零。 ( ) 0 A 矢量场的旋度之散度恒等于零