
KKT条件 当强对偶性成立时,令x*和α*,b*分别是原问题和对偶问题的最优解,那么 它们满足以下条件: M N 梯度条件: 7f(x)+∑ain Vhm(x)+∑bVgn(*)=0, (C.23) m=1 n=1 原始可行性条件:hm(x*)=0, m=1,…,M (C.24) gn(x*)≤0, n=1,…,N (C.25) 互补松弛条件:b*gn(x*)=0, n=1,…,N (C.26) 对偶可行性条件:b≥0, n=1,…,W (C.27) 这5个条件称为不等式约束优化问题的KKT条件(Karush-Kuhn-Tucker Con- dition).KKT条件是拉格朗日乘数法在不等式约束优化问题上的泛化.当原问 题是凸优化问题时,满足KKT条件的解也是原问题和对偶问题的最优解。 16
KKT条件 16

Outline ·4.3补充:优化算法NNDL《神经网络与深度学习 》附录p418-425 ·4.3支持向量机 ·4.4朴素贝叶斯分类器 哈尔滨工业大学计算机学院刘远超 17
Outline • 4.3 补充:优化算法NNDL《神经⽹络与深度学习 》附录p418-425 • 4.3 ⽀持向量机 • 4.4 朴素⻉叶斯分类器 哈尔滨工业大学计算机学院 刘远超 17

大纲 ▣间隔与支持向量 口对偶问题 ▣核函数 口软间隔与正则化 ▣核方法
大纲 p 间隔与支持向量 p 对偶问题 p 核函数 p 软间隔与正则化 p 核方法
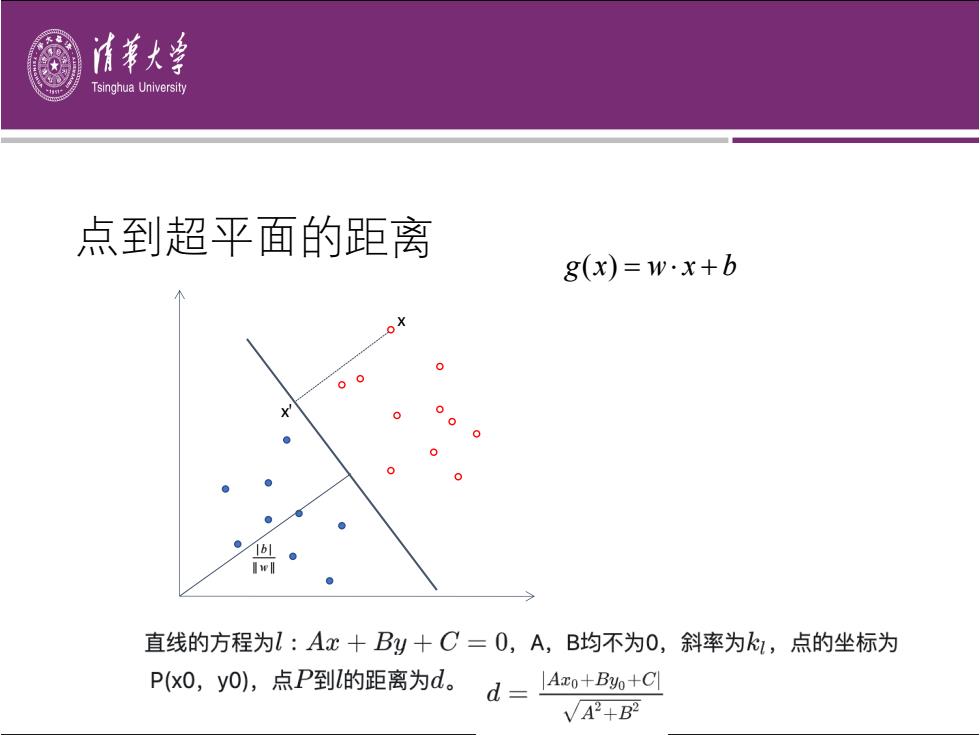
清第大多 Tsinghua University 点到超平面的距离 8(x)=w·x+b 0 16/ 直线的方程为l:Ax十By十C=0,A,B均不为0,斜率为k1,点的坐标为 P(x0,yO),点P到l的距离为d。d=lAo+B+C VA2+B
x x' g(x) = w× x + b || || | | w b 点到超平⾯的距离

门第大多 Tsinghua University 函数间隔和几何间隔 ·点到分离超平面的远近|wx+b ● →表示分类预测的确信程度 ·wx+b的符号与类标记y的符号是否一致 →表示分类是否正确 ·所以: ·y(w…x+b)表示分类的正确性和确信度
• 点到分离超平⾯的远近 • 表示分类预测的确信程度 • 的符号与类标记y的符号是否⼀致 • 表示分类是否正确 • 所以: • 表示分类的正确性和确信度 函数间隔和⼏何间隔