
第八章现代光学基础 1960年5月美国休斯公司的梅曼成功地做出了第 台红宝石泊光器,我们才真正地找 到了一个光源。“激光”是光受激射放大的简称。它具有单色性佳,亮度高,相干性强,方 向性好的特点。目前,在激光理论,激光技术,激光应用等各个方面,都取得了巨大进展, 而且带动了全息光学,非线性光学,傅里叶光学,激光光谱光,光化学,光通讯,光存贮, 光信息等新兴学科的发展。 我国激光器1961年9月问世:长春光学精密机械研究所,王之江领导设计并和邓锡 铭、汤显里、杜继禄等共同实验研制成的。钱学森1964年12月建议“激光”,在第三届光 受激辐射学术会议上通过。 本章主要讲激光原理,介绍全息技术等现代光学概念。 §8-1 原子发光的机理 一、玻尔的氢原子模型 图8-1 ze2 (1) 玻尔引用量子论,提出一个假设: 电子的角动量,风能等于公的整数告, mir=n n(主量子数)=,2,3,. (2) 2π 由(1)和(2)式得: 方2 r=n4产mek (3) 0-2e6 (4) i
第八章 现代光学基础 1960 年 5 月美国休斯公司的梅曼成功地做出了第一台红宝石泊光器,我们才真正地找 到了一个光源。“激光”是光受激射放大的简称。它具有单色性佳,亮度高,相干性强,方 向性好的特点。目前,在激光理论,激光技术,激光应用等各个方面,都取得了巨大进展, 而且带动了全息光学,非线性光学,傅里叶光学,激光光谱光,光化学,光通讯,光存贮, 光信息等新兴学科的发展。 我国激光器 1961 年 9 月问世:长春光学精密机械研究所,王之江领导设计并和邓锡 铭、汤显里、杜继禄等共同实验研制成的。钱学森 1964 年 12 月建议“激光”,在第三届光 受激辐射学术会议上通过。 本章主要讲激光原理,介绍全息技术等现代光学概念。 §8—1 原子发光的机理 一、玻尔的氢原子模型 图 8-1 2 0 2 2 2 2 4 r ze r ze k r m (1) 玻尔引用量子论,提出一个假设: 电子的角动量 mr ,只能等于 2 的整数倍。 2 m r n n(主量子数)=1,2,3,. (2) 由(1)和(2)式得: me zk r n 2 2 2 2 4 (3) n e zk 2 2 (4)
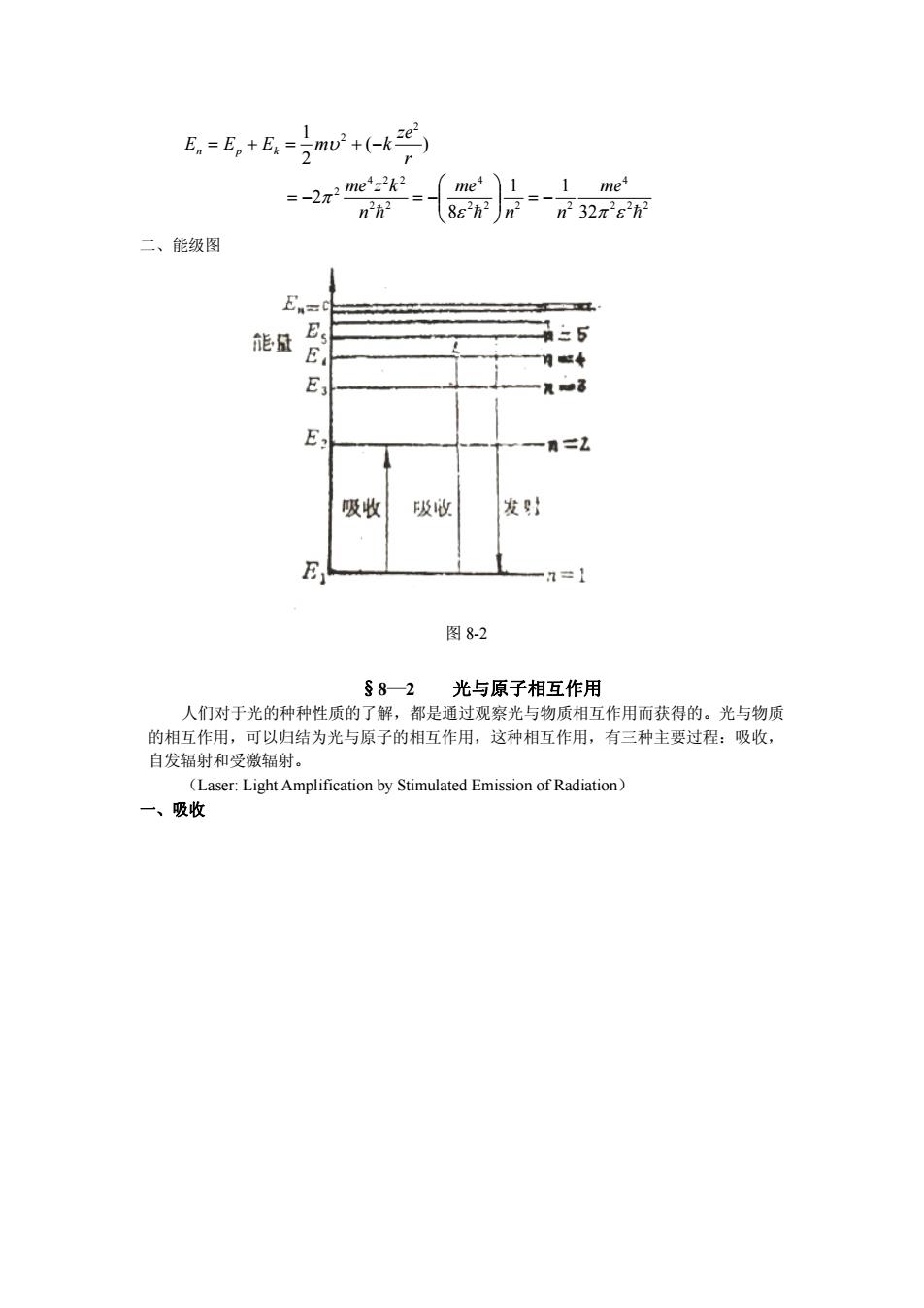
£=E,+=u2+(-kS =-2n2 me = me) n'n2 {)片7 二、能级图 E 能盆 5 E 吸收 吸收 发 -7=1 图8-2 §8一2光与原子相互作用 人们对于光的种种性质的了解,都是通过观察光与物质相互作用而获得的。光与物质 的相互作用, 圆的结为光与原子的相互作用,这种相互作用,有气种主惑过程:吸收: 自发辐射和受 (Laser:Light Amplification by Stimulated Emission of Radiation 一、吸收
2 2 2 4 2 2 2 2 4 2 2 4 2 2 2 2 2 32 1 1 8 2 ( ) 2 1 me n n me n me z k r ze E E E m k n p k 二、能级图 图 8-2 §8—2 光与原子相互作用 人们对于光的种种性质的了解,都是通过观察光与物质相互作用而获得的。光与物质 的相互作用,可以归结为光与原子的相互作用,这种相互作用,有三种主要过程:吸收, 自发辐射和受激辐射。 (Laser: Light Amplification by Stimulated Emission of Radiation) 一、吸收

0) 图8-3 如果有一个原子,开始时处于基态E,若没有外来光子接近它,则它将保持不变。如 果有一个能量为y,的光子接近这个原子,则它就有可能吸收这个光子,从而提高它的能 量状态。在吸收过程中,不是任何能量的光子都能被一个原子所吸收,只有当光子的能量 正好等于原子的能级间隔E?一E时,这样的光子才能被吸收 hva E2 -E 设处于基态E,的原子密度为m,光的辐射能量密度为(),则单位体积单位时间内 吸收光子而跃迁到激发态B2去的原子数n2应该与m1和()成正比: n2ocn,uv) n2=B2nu(y) B12称为受激吸收爱因斯坦系数。B2(v)称为吸收速率 令w2=B2() 几12=n11W2 二、自发辐射 从经典力学的观点来讲,一个物体如果势能很高,它将是不稳定的。与此相类似,处 于激发态的原子也是不稳定的,它们在激发态停留的时间一般都非常短,大约为10s的数 量级,所以我们常常说激发态的寿命约为10 在 受外界的影响时,它们会自发地返回 到基态去,从而放出光子。这种自发地从激发态返回较低能态而放出光子的过程,叫做自 发辐射过程。 处于激发态E2的原子密度为2,则自发辐射光子数为
图 8-3 如果有一个原子,开始时处于基态 E1,若没有外来光子接近它,则它将保持不变。如 果有一个能量为 21 的光子接近这个原子,则它就有可能吸收这个光子,从而提高它的能 量状态。在吸收过程中,不是任何能量的光子都能被一个原子所吸收,只有当光子的能量 正好等于原子的能级间隔 E2—E1 时,这样的光子才能被吸收 21 E2 E1 设处于基态 E1 的原子密度为 n1,光的辐射能量密度为u( ) ,则单位体积单位时间内 吸收光子而跃迁到激发态 E2 去的原子数 n12 应该与 n1 和u( ) 成正比: ( ) ( ) 12 12 1 12 1 n B n u n n u B12 称为受激吸收爱因斯坦系数。 ( ) B12u 称为吸收速率 令 12 12 12 1 12 w B u( ) n n w 二、自发辐射 从经典力学的观点来讲,一个物体如果势能很高,它将是不稳定的。与此相类似,处 于激发态的原子也是不稳定的,它们在激发态停留的时间一般都非常短,大约为 10-8 s 的数 量级,所以我们常常说激发态的寿命约为 10-8 s。在不受外界的影响时,它们会自发地返回 到基态去,从而放出光子。这种自发地从激发态返回较低能态而放出光子的过程,叫做自 发辐射过程。 处于激发态 E2 的原子密度为 n2,则自发辐射光子数为

n21=n2A21 4:为自发辐射爱因斯坦系数 各个原子的辐射都是自发地,独立地进行的,因而各个原子发出来的光子在发射方向 和初位相上都是不相同的,普通光源的发光都属于自发辐射。普通光源发出来的光,其频 率成份极为复杂,发射方向分散在4π立体角内,初位相也各不相同,因而不是相干光。 三、受激辐射 1917年,爱因斯坦从纯粹的热力学出发,用具有分立能级的原子模型来推导普朗克辐 射公式,在这 工作中,爱因斯坦预言了受激辐射的存在。四十年以后,第一台激光器开 始运转,爱因斯坦的这一预言得到了证实。 图8-4 处于激发态的原子,如果在外来光子的影响下,引起从高能态向低能态的跃迁,并把 两个状态之间的能量差以辐射光子的形式发射出去,这种过程叫做受激发射。受激辐射原 子数为: 5:=B2,n(v) B2:受激辐射爱因斯坦系数,B2y)称为受激辐射速率。用W21表示 只有当外来光子的能量2=E2-E,时,才能引起受激辐射。而且受激辐射发出来 的光子与外来光子具有相同的频率,相同的辐射方向,相同的偏振态和相同的位相。 四、吸收、自发辐射和受激辐射三系数之间的关系 当光子和原子相互作用时,同时存在若吸收,自发辐射和受激辐射三种过程,达到平 衡时,单位体积单位时间内跃迁到激发态去的原子数,等于从激发态通过自发辐射和受激 辐射跃迁回基态的原子数,在平衡条件下有 n2=n21+51 m Bzu(v)=nA+n Bau(v) )= A h Bua B
21 2 A21 n n A21 为自发辐射爱因斯坦系数 各个原子的辐射都是自发地,独立地进行的,因而各个原子发出来的光子在发射方向 和初位相上都是不相同的,普通光源的发光都属于自发辐射。普通光源发出来的光,其频 率成份极为复杂,发射方向分散在 4 立体角内,初位相也各不相同,因而不是相干光。 三、受激辐射 1917 年,爱因斯坦从纯粹的热力学出发,用具有分立能级的原子模型来推导普朗克辐 射公式,在这一工作中,爱因斯坦预言了受激辐射的存在。四十年以后,第一台激光器开 始运转,爱因斯坦的这一预言得到了证实。 图 8-4 处于激发态的原子,如果在外来光子的影响下,引起从高能态向低能态的跃迁,并把 两个状态之间的能量差以辐射光子的形式发射出去,这种过程叫做受激发射。受激辐射原 子数为: ( ) n21 B21n2u B21:受激辐射爱因斯坦系数, ( ) B21u 称为受激辐射速率。用W21表示 21 2W21 n n 只有当外来光子的能量 21 E2 E1 时,才能引起受激辐射。而且受激辐射发出来 的光子与外来光子具有相同的频率,相同的辐射方向,相同的偏振态和相同的位相。 四、吸收、自发辐射和受激辐射三系数之间的关系 当光子和原子相互作用时,同时存在着吸收,自发辐射和受激辐射三种过程,达到平 衡时,单位体积单位时间内跃迁到激发态去的原子数,等于从激发态通过自发辐射和受激 辐射跃迁回基态的原子数,在平衡条件下有 12 21 21 n n n ( ) ( ) n1B12u n2 A21 n2B21u 12 21 2 1 21 ( ) B B n n A u

在处于热平衡状态下,粒子数密度按能量的分布遵从玻尔兹曼定律,即: 因E2>E, 氖原子的某一激发态和基态能级的能量差△正=6.9cy =e=西=0 1 1 A (v)BeBa 对于黑体辐射来说,在热平衡状态时,腔内的辐射场应是不随时间变化的稳定分布 有 8"n一Be-AB2。一1 B21 则:B2=B21=B 会” §8-3 粒子数反转 一、受激辐射与吸收 激光就是通过辐射的受源程序发射来实现光放大的。一个光子“射入一个原子体系 以后,在离开该原子体系时,成了两个或更多个光子,而且这些光子的特征是完全相同的, 这就实现了光放大。但是光与原子相互作用时,总是同时存在着吸收,自发辐射和受激辐 射三种过程。问题在于什么条件下受激辐射占主导地位。 单位时间,单位体积内原子体系吸收的光能量为n,()B防v,受激辐射产生的光能 量为n(v)B防y,所以单位时间单位体积产生的净光能量为(m,-n)u(y)B防y,设此原 子体系的体积元为,截面积为5,1为辐射作用时间,山表示光能量的变化,则单位体 积单位时间产生的净光能量可表示为 高-是=-ar
在处于热平衡状态下,粒子数密度按能量的分布遵从玻尔兹曼定律,即: kT kT E E n n exp exp 2 1 1 2 因 1 1 2 2 1 n n E E 氖原子的某一激发态和基态能级的能量差 E 16.9 ev 0 1 653 653 1 2 e e n n 12 21 21 ( ) B e B A u v kT 对于黑体辐射来说,在热平衡状态时,腔内的辐射场应是不随时间变化的稳定分布。 有关系 1 1 4 8 1 ( ) 21 12 21 12 21 21 3 3 , 21 kT B v T kT kT e B B A B e B A c e h c u 则: B12 B21 B 3 3 21 21 8 B c A §8—3 粒子数反转 一、受激辐射与吸收 激光就是通过辐射的受源程序发射来实现光放大的。一个光子 射入一个原子体系 以后,在离开该原子体系时,成了两个或更多个光子,而且这些光子的特征是完全相同的, 这就实现了光放大。但是光与原子相互作用时,总是同时存在着吸收,自发辐射和受激辐 射三种过程。问题在于什么条件下受激辐射占主导地位。 单位时间,单位体积内原子体系吸收的光能量为 n1u( )B ,受激辐射产生的光能 量为 n2u( )B ,所以单位时间单位体积产生的净光能量为(n2 n1 )u( )B ,设此原 子体系的体积元为 dv ,截面积为 s ,t 为辐射作用时间,dj 表示光能量的变化,则单位体 积单位时间产生的净光能量可表示为 n n u B tsdz dj tdv dj ( ) ( ) 2 1 光强 ( ) cu( ) st j I