
第二章光的衍射 波动具有两大特性:干涉、衍射。现在我们根据光的衍射现象和实验事实进一步提示 光的波动性。说明衍射是光在空间或物质中传播的基本方式。同时也介绍衍射现象的几种重 要应用。 §2一1光的衍射现象 泰(好(6)⊙媒森戴d崖」 图21 光的干涉现象是几束光相互叠加的结果,让一束光通过狭缝投射在屏上。在影的中央, 应该是最暗的地方,实际观察到的却是亮的。光通过狭缝,其至经过任何物体的边缘,在不 同程度上都有类似的情况。这种光绕过障碍物偏离直线传播面进入几何阴影,并在屏幕上出 现光强不均匀的分布现象,叫做光的衍射。 衍射现象的出现与否,主要决定于障碍物线度和波长大小的对比,只有在障碍物线度和 波长可以比拟时,衍射现象才明显地表现出来。 §2一2惠更斯一菲涅耳原理 一、惠更斯原理 在研究波的传播时,总可以找到同位相各点的几何位置,这些点的轨迹是等相面,叫做 波面。惠更斯曾提出次波的假设来阐述波的传播现象,从而建立了惠更斯原理:任何时刻波 面上的每一点都可以作为次波的波源,各自发出球面次波:在其后的任何时刻,所有这些次 波波面的保络面形成整个波在该时刻的新波面。 根据这个原理,可以从某一时刻己知的波面位置,求出另一时刻波面的位置。可以解释 光的直线传播、反射、折射,还可解释晶体的双折射现象。但有倒退波的存在,也不能说明 有明暗相间条纹的出现
第二章 光的衍射 波动具有两大特性:干涉、 衍射。现在我们根据光的衍射现象和实验事实进一步提示 光的波动性。说明衍射是光在空间或物质中传播的基本方式。同时也介绍衍射现象的几种重 要应用。 §2—1 光的衍射现象 图 2-1 光的干涉现象是几束光相互叠加的结果,让一束光通过狭缝投射在屏上。在影的中央, 应该是最暗的地方,实际观察到的却是亮的。光通过狭缝,甚至经过任何物体的边缘,在不 同程度上都有类似的情况。这种光绕过障碍物偏离直线传播而进入几何阴影,并在屏幕上出 现光强不均匀的分布现象,叫做光的衍射。 衍射现象的出现与否,主要决定于障碍物线度和波长大小的对比,只有在障碍物线度和 波长可以比拟时,衍射现象才明显地表现出来。 §2—2 惠更斯—菲涅耳原理 一、惠更斯原理: 在研究波的传播时,总可以找到同位相各点的几何位置,这些点的轨迹是等相面,叫做 波面。惠更斯曾提出次波的假设来阐述波的传播现象,从而建立了惠更斯原理:任何时刻波 面上的每一点都可以作为次波的波源,各自发出球面次波;在其后的任何时刻,所有这些次 波波面的保络面形成整个波在该时刻的新波面。 根据这个原理,可以从某一时刻已知的波面位置,求出另一时刻波面的位置。可以解释 光的直线传播、反射、折射,还可解释晶体的双折射现象。但有倒退波的存在,也不能说明 有明暗相间条纹的出现

二、非涅耳对惠更斯原理的改进 菲涅耳根据惠更斯的“次波”假设,补充了描述次波的基本特征一位相和振幅的定 量表示式,并增加了“次波相干叠加”的原理,从而发展成为惠更斯一菲涅耳原理。这个 原理的内容表述如下: 波面。上每个面积元都可以看成新的波源,它们均发出次波,波面前方空间某一点 P的振动可以由s面上所有面积元发出的次波在该点叠加后的合振幅来表示。面积元山所 发出的各次波的振幅和位相符合下列四个假设: ds 图2-2 (1)波面是一个等位相面,因而可以认为本面上各点所发出的所有次波都有相同的 初位相(可令p=0) (2)次波在点处所引起的振动的振幅与r成反比,这相当于表明次波是球面波。 (3)从面积元d6所发次波在P点处的振幅正比于本的面积,且与倾角0有关,振幅 随0的增大而减小。 (4))次波在p点处的位相由光程△=m决定(0=2△) 根据以上的假设,可知面积d本发出的次波在P点的振动可表示为 dE=c()cos(kr-of)ds r K()随角增大而缓慢减小 如果波面上的各点振幅有一定的分布,分布函数为4(Q), 则:dE=eKO)A2cosk-ords 波面s在p点所产生的合振动为 Edcf)co 或E=cKo@bh 上式称为菲涅耳衍射积分,一般来说计算此积分式是相当复杂的,但在波面对于通过
二、菲涅耳对惠更斯原理的改进 菲涅耳根据惠更斯的“次波”假设,补充了描述次波的基本特征——位相和振幅的定 量表示式,并增加了“次波相干叠加”的原理,从而发展成为惠更斯—菲涅耳原理。这个 原理的内容表述如下: 波面 s 上每个面积元 ds 都可以看成新的波源,它们均发出次波,波面前方空间某一点 p 的振动可以由 s 面上所有面积元发出的次波在该点叠加后的合振幅来表示。面积元 ds 所 发出的各次波的振幅和位相符合下列四个假设: 图 2-2 (1) 波面是一个等位相面,因而可以认为 ds 面上各点所发出的所有次波都有相同的 初位相(可令 0 ) (2) 次波在 p 点处所引起的振动的振幅与 r 成反比,这相当于表明次波是球面波。 (3) 从面积元 ds 所发次波在 p 点处的振幅正比于 ds 的面积,且与倾角θ有关,振幅 随θ的增大而减小。 (4) 次波在 p 点处的位相由光程 nr 决定( 2 ) 根据以上的假设,可知面积 ds 发出的次波在 p 点的振动可表示为 kr t ds r K dE c cos( ) ( ) K( ) 随θ角增大而缓慢减小 如果波面上的各点振幅有一定的分布,分布函数为 A(Q) , 则: kr t ds r K A Q dE c cos( ) ( ) ( ) 波面 s 在 p 点所产生的合振动为 s s kr t ds r K A Q E dE c cos( ) ( ) ( ) 或 s i kr t ds r K A Q E c ( ) ( ) ( ) 上式称为菲涅耳衍射积分,一般来说计算此积分式是相当复杂的,但在波面对于通过 p
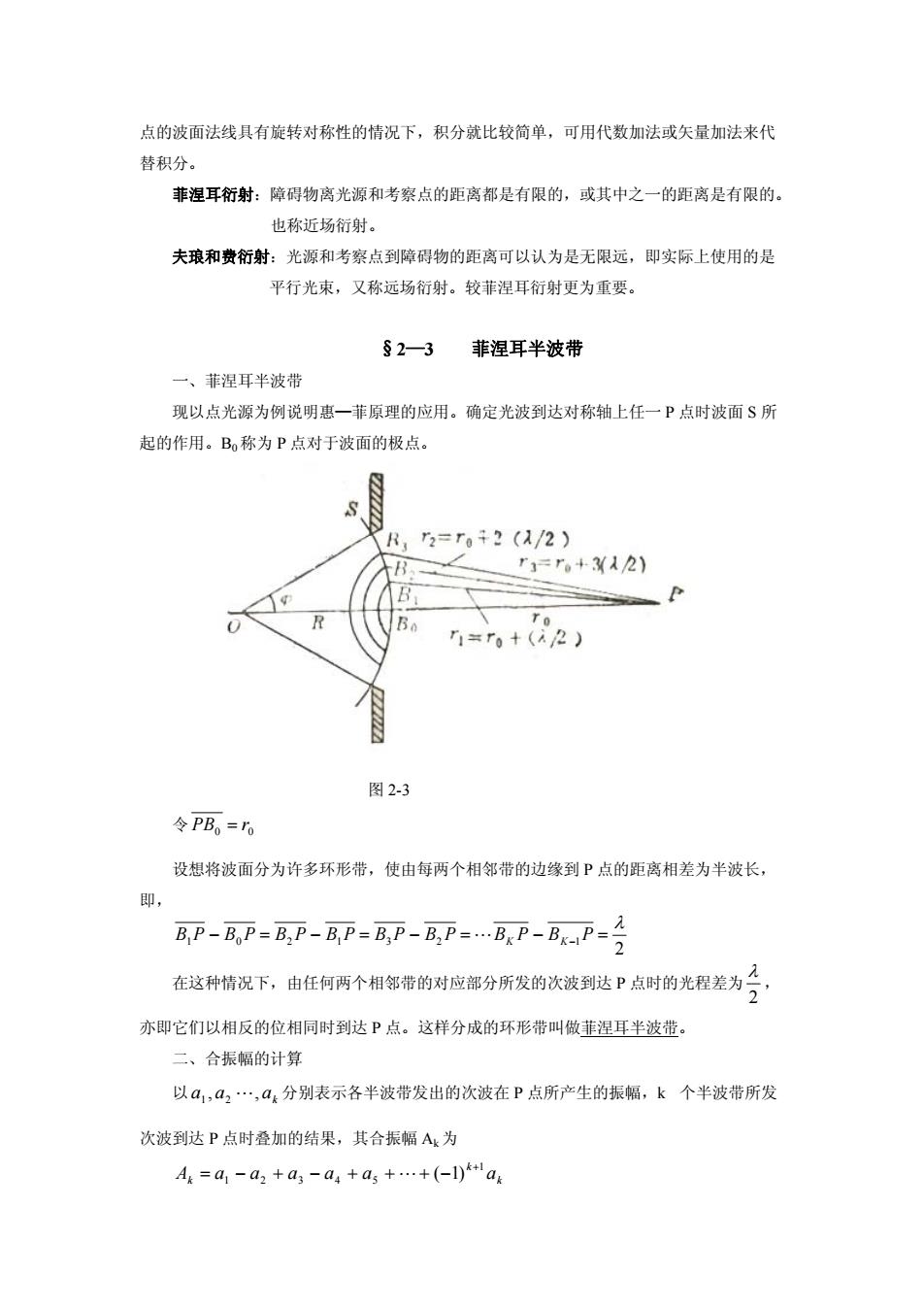
点的波面法线具有旋转对称性的情况下,积分就比较简单,可用代数加法或矢量加法来代 替积分。 菲涅耳衍射:障碍物离光源和考察点的距离都是有限的,或其中之一的距离是有限的。 也称近场衍射。 夫琅和费衍射:光源和考察点到障碍物的距离可以认为是无限远,即实际上使用的是 平行光束,又称远场衍射。较菲涅耳衍射更为重要。 §2-3 菲涅耳半波带 一、菲涅耳半波带 现以点光源为例说明惠一菲原理的应用。确定光波到达对称轴上任一P点时波面S所 起的作用。B称为P点对于波面的极点。 r32=r02(/2) r1=”。+3XA2) 图2-3 令PB。=0 设想将波面分为许多环形带,使由每两个相邻带的边缘到P点的距离相差为半波长, 即 BP-B.P-B,P-B.P-B,P-B,P-.B.P-BxaP 在这种情况下,由任何两个相邻带的对应部分所发的次波到达P点时的光程差为 亦即它们以相反的位相同时到达P点。这样分成的环形带叫做菲涅耳半波 二、合振幅的计算 以a1,a,a分别表示各半波带发出的次波在P点所产生的振幅,k个半波带所发 次波到达P点时叠加的结果,其合振幅A为 A=a1-a2+a3-a4+a5+.+(-l)la
点的波面法线具有旋转对称性的情况下,积分就比较简单,可用代数加法或矢量加法来代 替积分。 菲涅耳衍射:障碍物离光源和考察点的距离都是有限的,或其中之一的距离是有限的。 也称近场衍射。 夫琅和费衍射:光源和考察点到障碍物的距离可以认为是无限远,即实际上使用的是 平行光束,又称远场衍射。较菲涅耳衍射更为重要。 §2—3 菲涅耳半波带 一、菲涅耳半波带 现以点光源为例说明惠—菲原理的应用。确定光波到达对称轴上任一 P 点时波面 S 所 起的作用。B0 称为 P 点对于波面的极点。 图 2-3 令 0 0 PB r 设想将波面分为许多环形带,使由每两个相邻带的边缘到 P 点的距离相差为半波长, 即, 2 1 0 2 1 3 2 1 B P B P B P B P B P B P BK P BK P 在这种情况下,由任何两个相邻带的对应部分所发的次波到达 P 点时的光程差为 2 , 亦即它们以相反的位相同时到达 P 点。这样分成的环形带叫做菲涅耳半波带。 二、合振幅的计算 以 a a ak , , 1 2 分别表示各半波带发出的次波在 P 点所产生的振幅,k 个半波带所发 次波到达 P 点时叠加的结果,其合振幅 Ak 为 k k Ak a a a a a a 1 1 2 3 4 5 ( 1)

0 a→p 图2-4 按惠一菲原理: k()AS 为了计算△S,我们看下面的球冠,其面积为 r S=2πR·Rl-cosp)=2πR21-cosp) 而c0sp=R+R+62- 2R(R+) 将上列两式分别微分,得 ds=2xRsin odo sindo=RR+o】 rdrs 因为》元,可将山视作子,面6即为半被带的面积,于是4S=R2 nR+r。 。由此 可知△S与k无关。即它对每个半波带都是相同的。影响A大小的因素中只剩下倾斜因子 k(0:),从一个半波带到邻近一个半波带,0,的数值变化甚微,因而k(0)和a,随k的增 加而缓慢地减小
图 2-4 按惠—菲原理: k k k k r S a k ( ) 为了计算 k k r S ,我们看下面的球冠,其面积为 2 (1 cos ) 2 (1 cos ) 2 S R R R 而 2 ( ) ( ) cos 0 2 2 0 2 R R r R R r rk 将上列两式分别微分,得 ( ) sin 2 sin 0 2 R R r r dr d ds R d k k 则 k k dr R r R r ds 0 2 因为 rk ,可将 drk视作 2 ,而 ds 即为半波带的面积,于是 0 R r R r S k k 。由此 可知 k k r S 与 k 无关。即它对每个半波带都是相同的。影响 Ak 大小的因素中只剩下倾斜因子 ( ) k k ,从一个半波带到邻近一个半波带,k 的数值变化甚微,因而 ( ) k k 和 ak 随 k 的增 加而缓慢地减小
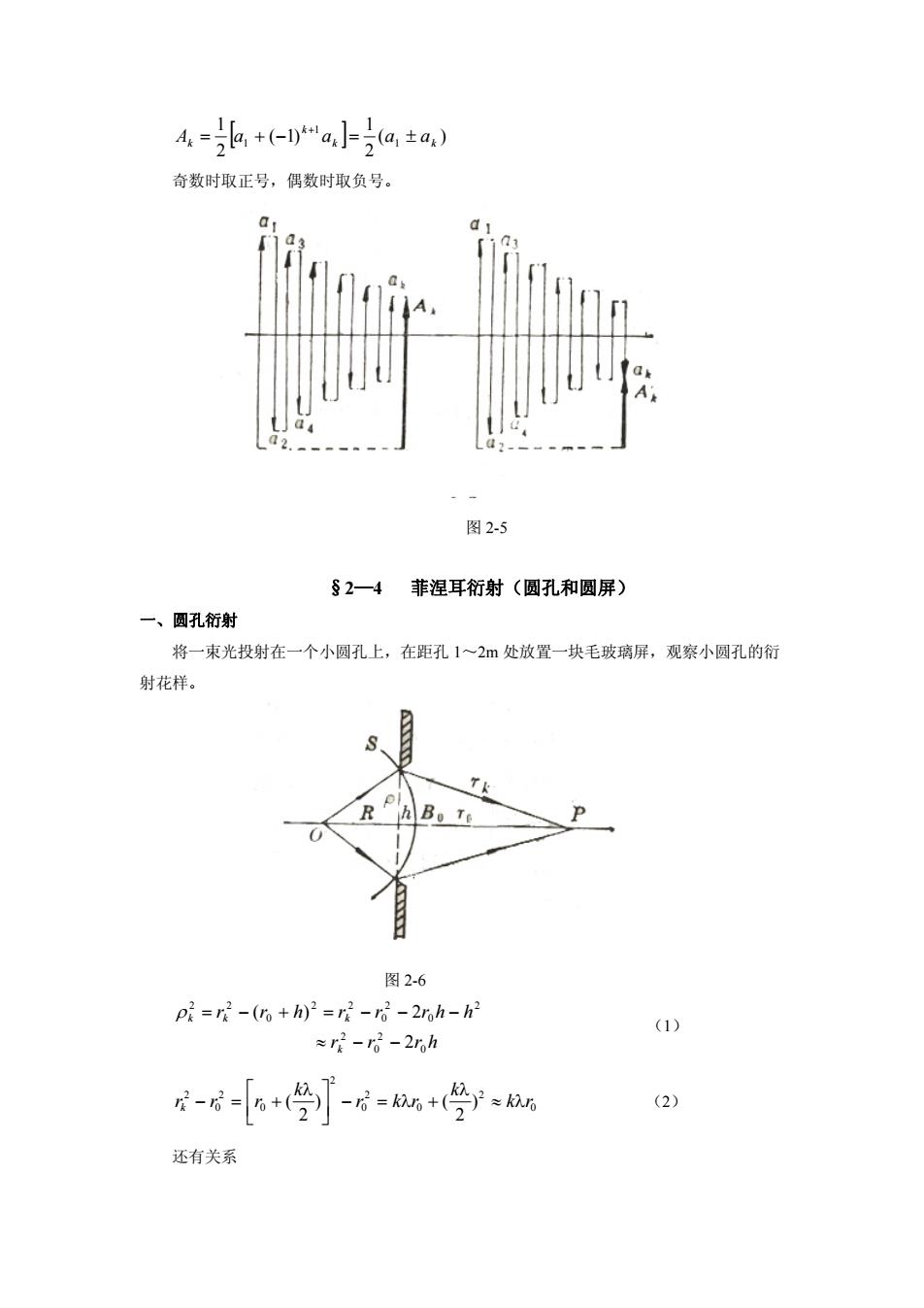
A=k,+a小a±a) 奇数时取正号,偶数时取负号。 图2-5 §2一4菲涅耳衍射(圆孔和圆屏) 一、圆孔衍射 将一束光投射在一个小圆孔上,在距孔1~2m处放置一块毛玻璃屏,观察小圆孔的衍 射花样。 图2-6 p=r2-(。+h)2=r-r-2h-h2 (1) ≈r-r-2rh 才-6+学∫-8-+学 (2) 还有关系
( ) 2 1 ( 1) 2 1 1 1 1 k k k Ak a a a a 奇数时取正号,偶数时取负号。 图 2-5 §2—4 菲涅耳衍射(圆孔和圆屏) 一、圆孔衍射 将一束光投射在一个小圆孔上,在距孔 1~2m 处放置一块毛玻璃屏,观察小圆孔的衍 射花样。 图 2-6 r r r h r r h r r r h h k k k k 0 2 0 2 2 0 2 0 2 2 0 2 2 2 ( ) 2 (1) 0 2 0 2 0 2 0 2 0 2 ) 2 ) ( 2 ( k r k r k r k r r r k (2) 还有关系