《光学》课程授课教案（讲义）光的干涉

光学第一章光的干涉 第一章光的干涉 §1.1两列单色波的干涉花样 一.两个点光源的干涉 球面波，在场点P相遇，则有 (x.y.z) S =A cost(k -o+a)=4 cos(o+ v-4.co.coo 可设初位相均为零，则位相差 4p-受w5-W 光程差 6=n25-n5 在真空中 - 干涉相长： 0:-2g用8=6-4=a 干涉相消： 2 仍-)=2+z即6=5-万=2j+)号 0,±1，土2，士3，土4，.被称做干涉级数 亮条纹和暗条纹在空间形成一系列双叶旋转双曲面。在平面接收屏上为一组双曲线，明 暗交错分布。干涉条纹为非定域的，空间各处均可见到

光学 第一章 光的干涉 第一章 光的干涉 § 1.1 两列单色波的干涉花样 一．两个点光源的干涉 球面波，在场点 P 相遇，则有 ) 2 cos( cos() 11 11 01 1 11  01       trnAtrkA  ) 2 cos( cos() 22 22 02 2 22  02       trnAtrkA  可设初位相均为零，则位相差 ( 22  2 rn    )11rn 光程差 1122   rnrn 在真空中 )( 2 12  rr    干涉相长： (r 2   2 )1  r  2 j 即   12  jrr  干涉相消： 2 ( 2 r   )1  r  j  )12(  即   rr 12  2 )12(  j  j=0， 1， 2，  3，  4，.被称做干涉级数。 亮条纹和暗条纹在空间形成一系列双叶旋转双曲面。在平面接收屏上为一组双曲线，明 暗交错分布。干涉条纹为非定域的，空间各处均可见到。 1

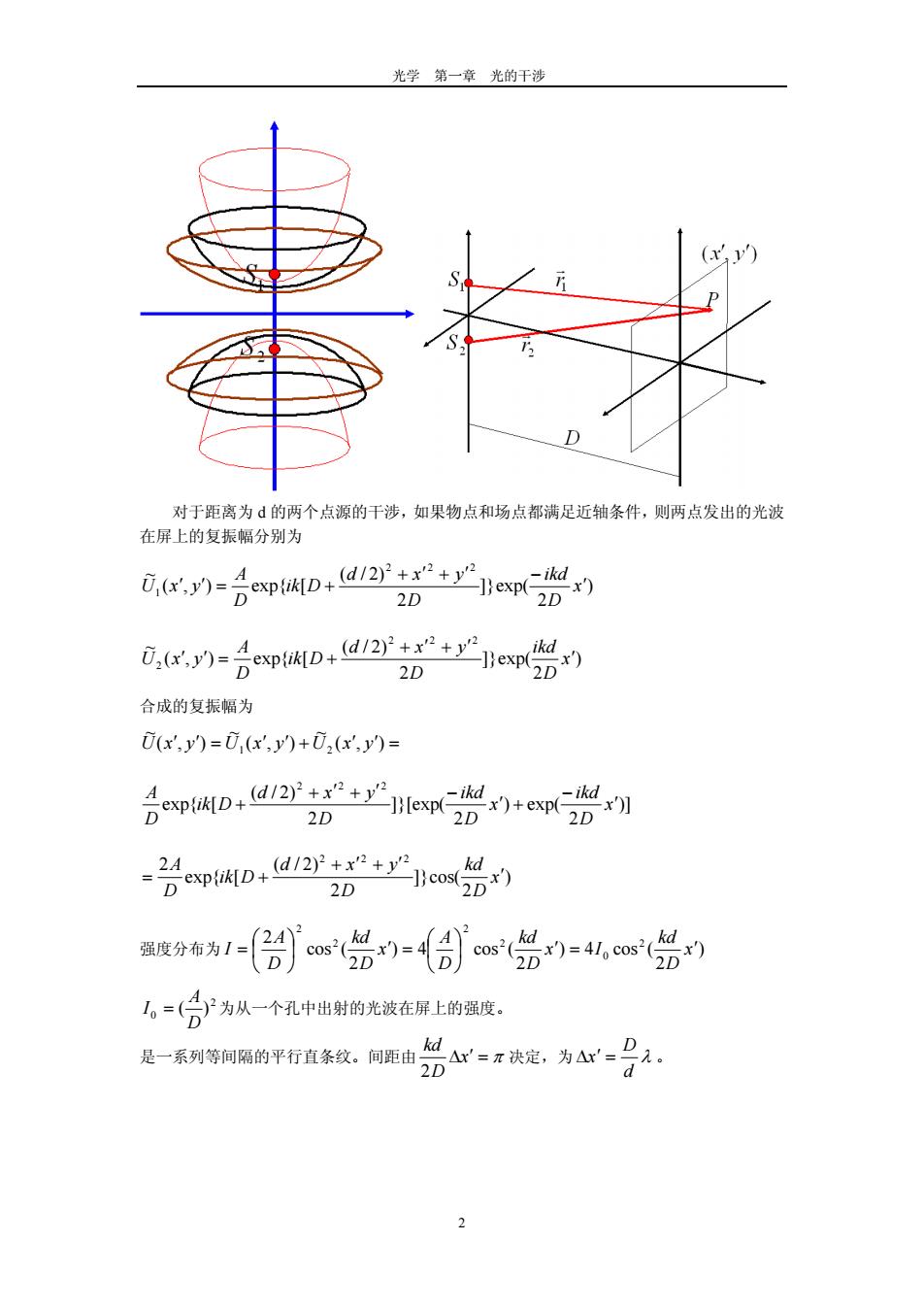
光学第一章光的干涉 对于距离为的两个点源的干涉，如果物点和场点都满足近轴条件，则两点发出的光波 在屏上的复振幅分别为 00=Ap0ta12'8+e0 2D 元n-Apo,2+yjc% 2D 合成的复振幅为 0(x,y=0,(x,y)+02(x,y)= 合p0,2若e兴+am d 2D w0,2=号 2D 1,=(号？为从一个孔中出射的光被在屏上的强度。 是一系到等间隔的平行直条纹。间距由品A。:淡定，为4一号

光学 第一章 光的干涉 对于距离为 d 的两个点源的干涉，如果物点和场点都满足近轴条件，则两点发出的光波 在屏上的复振幅分别为 ) 2 exp(]} 2 )2/( [exp{),( ~ 222 1 x D ikd D yxd Dik D A yxU          ) 2 exp(]} 2 )2/( [exp{),( ~ 222 2 x D ikd D yxd Dik D A yxU         合成的复振幅为      ),(  ~ ),( ~ ),( ~ 1 2 yxUyxUyxU )] 2 exp() 2 ]}[exp( 2 )2/( [exp{ 222 x D ikd x D ikd D yxd Dik D A           ) 2 cos(]} 2 )2/( [exp{ 2 222 x D kd D yxd Dik D A        强度分布为 ) 2 (cos4) 2 (cos4) 2 (cos 2 2 0 2 2 2 2 x D kd Ix D kd D A x D kd D A I                   2 0 )(D A I  为从一个孔中出射的光波在屏上的强度。 是一系列等间隔的平行直条纹。间距由 x   D kd 2 决定，为  d D x  。 2

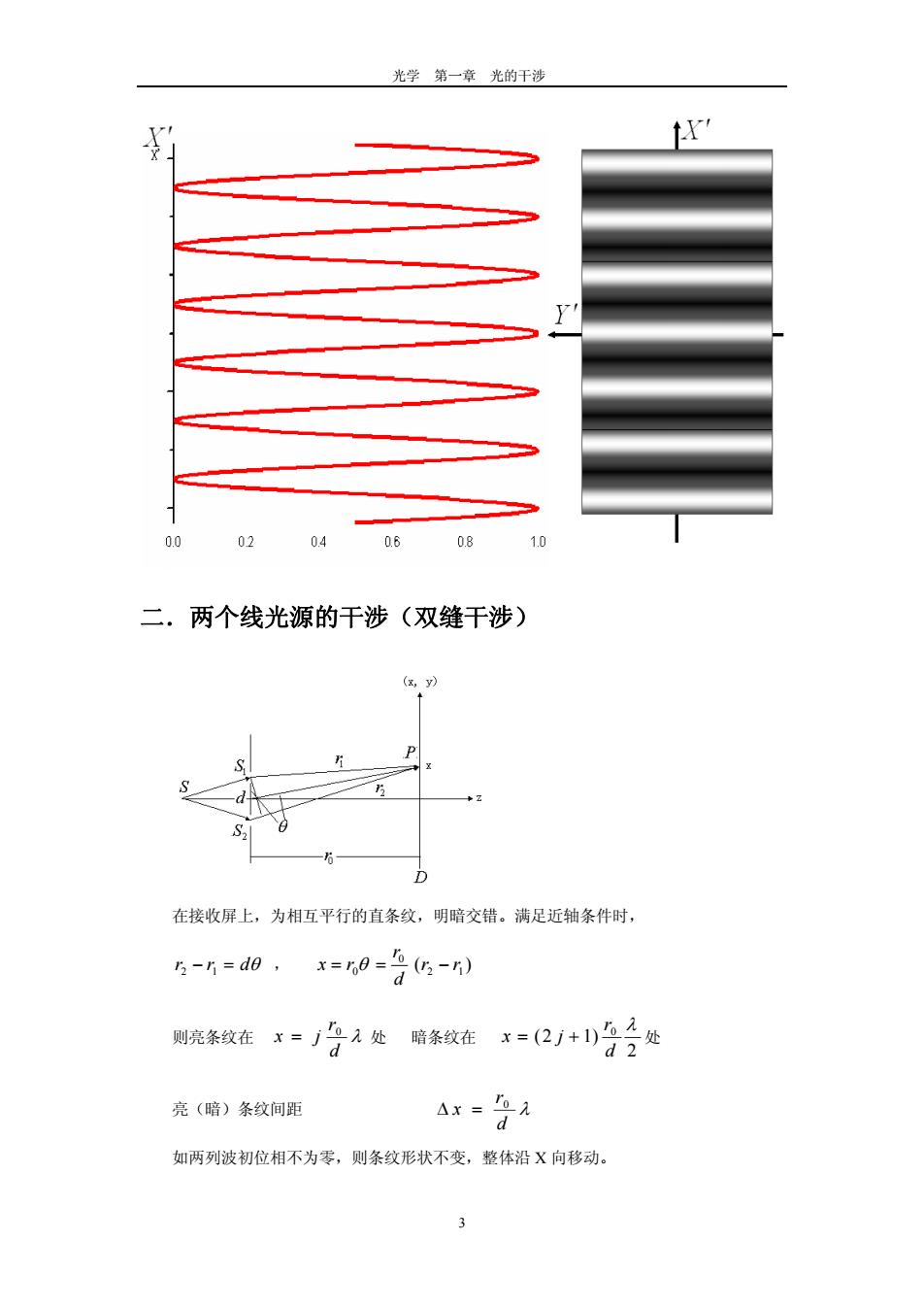
光学第一章光的干涉 0.0 02 0406 08 10 二.两个线光源的干涉（双缝干涉） 在接收屏上，为相互平行的直条纹，明暗交错。满足近轴条件时 5-片=d0，x=r0=号G-) 则院条纹在=J合入处暗条纹在水=（口+小学径处 亮（暗）条纹间距 Ax=22 如两列波初位相不为零，则条纹形状不变，整体沿X向移动

光学 第一章 光的干涉 二．两个线光源的干涉（双缝干涉） 在接收屏上，为相互平行的直条纹，明暗交错。满足近轴条件时， rr 12  d ，  rx 0 d r0  )( 12  rr 则亮条纹在  d r jx 0  处 暗条纹在 2 )12( 0  d r jx  处 亮（暗）条纹间距  d r x 0  如两列波初位相不为零，则条纹形状不变，整体沿 X 向移动。 3

光学第一章光的干涉 如先海和装收保之同充满介质，因为￥=：沿-名 ,则条纹间距为 Ax=,n为折射率。 d n 干涉条纹为非定域的，接收屏在各处均可看到条纹。 三.干涉条纹的反衬度（可见度） 反衬度的定义：在接收屏上一选定的区域中，取光强最大值和最小值，有 而1y=(4+A2)2,1m=(4,-A2)月 24 则有y=244 当A1=A,时，Y=:当A1<A,或A>A2时，即41、A2相差悬殊时，Y=0. 记。+2，则条纹亮度可表示为 1=4+42+2A40s4p=(42+420+244 cos(+ycosA) 四.两束平行光的干涉 两列同频率单色光，。振幅分别为A1,A2:初位相为p0,P0,方向余弦角为(a1,B,乃)， (a42,B2,2)

光学 第一章 光的干涉 如光源和接收屏之间充满介质，因为 nd D j kd D jx     2 ，则条纹间距为 nd r x 0   ， n 为折射率。 干涉条纹为非定域的，接收屏在各处均可看到条纹。 三．干涉条纹的反衬度（可见度） 反衬度的定义：在接收屏上一选定的区域中，取光强最大值和最小值，有 mM mM II II     而 2 21 2 21 AAIAAI )(,)( M  m  则有 2 2 2 1 21 2 AA AA    2 2 1 2 1 )(1 2 A A A A   ， 当A1=A2时，γ=1；当A1<<A2或A1>>A2时，即A1、A2相差悬殊时，γ=0。 记I0=I1+I2，则条纹亮度可表示为 )cos1(]cos 2 1)[(cos2 2 0 2 2 1 2 21 2 2 21 1 2 2 2 1       I AA AA AAAAI AA 四．两束平行光的干涉 两列同频率单色光，。振幅分别为A1，A2；初位相为10 ， 20，方向余弦角为（ 111   ,  ）， （ 222   ,  ） 4

光学第一章光的干涉 x.V 在Z=0的波前上的位相为， (x.y)=k(cosa x+cosBy+cosy*0)+ 2(x.y)=k(cosazx+cos B2y+cosy2*0)+o 位相差△p(x,y)=k(cosa1-cosa,)x+k(cosB2-cosB)y+(p0-po) (x,y)处的强度为 I(x.y)=A2+2+244 cosA=(A2+A22)[1+ycosAo(x.y)] 可得干涉条纹 △pk,0=kcosa,-cosa)+k(cos月-cos月y+p-po)产{2)+lr 2iπ 即亮、暗条纹都是等间隔的平行直线，形成平行直线族，斜率为 cosa2 -cosa cos B,-cosB 条纹间隔为 2开 Ax=k(coscoscosa-cos Ay=k(B.-cos 1 或条纹的空间频率为{

光学 第一章 光的干涉 在 Z=0 的波前上的位相为， 1 1 1 1 10   (cos),(   cos  yxkyx    )0cos  2 2 2 2 20   (cos),(   cos  yxkyx    )0cos  位相差 (cos),( (cos)cos )()cos  1  1   2  1   1020 kyx kx y （x，y）处的强度为 ),( )],(cos1)[(cos2 2 2 2 21 1 2 2 2 1  AAAAyxI  AA   yx 可得干涉条纹 (cos),( (cos)cos )()cos  1  1   2  1   1020 kyx kx y =       )12( 2 j j 即亮、暗条纹都是等间隔的平行直线，形成平行直线族，斜率为 2 1 2 1 coscos coscos      条纹间隔为                2 1 2 1 2 1 2 1 (cos coscos)cos 2 (cos coscos)cos 2         k y k x 或条纹的空间频率为            y f x f y x 1 1 5