
第2章线条图处理技术 ·27· 利用对象形状及其属性的描述函数构造图形之后,图形软件包将选定视图投影 到输出设备。观察变换用来指定将要显示的视图使用的投影类型,以及在输出显示 区域出现的范围。 交互式图形应用多类输人设备,如鼠标、数据板或操纵杆。输入函数用于控制和 处理来自这些交互设备的数据流。 最后,图形软件包常常包含许多事务性任务,如将显示屏设成指定颜色和初始化 参数等,这类处理事务性任务的功能归人控制操作(control operation)类。 3.OpenGL简介 OpenGL基本函数库用来描述图元、属性、几何变换、观察变换,以及许多其他的 操作。OpenGL被设计成与硬件无关,因此输入和输出函数等许多操作均不包括在 其基本库中,但在为OpenGL开发的辅助库中有输人和输出函数及许多附加函数。 OpenGL系统由独立于设备的函数集(称为核心库)、实用库(GLU)和实用工具包 (GLUT)三部分构成。使用OpenGL基本库中的函数可以生成点、直线段、凸多边形 填充区和位图或像素图的图案阵列。在GLUT中有大量的函数用来管理显示窗口 与屏幕窗口系统的交互及生成某些三维形体。 OpenGL画点函数glVertex2i()指定一个点位置的坐标值,一个二维点位置的 OpenGL描述形式为: glBegin(GL_POINTS): glVertex2i(); glEnd(); 除了glRect函数外,顶点、线段或多边形的每一个位置均在glVertex函数中指 定。定义每一图元的一组glVertex函数用一对语句glBegin/glEnd()来包含,其中 glBegin()函数的变量用来指定要显示的输出图元的类型,glEnd()没有变量。例如 如果在glBegin()中使用图元线常量GL_LINES,可以实现画线功能。当然,Open- GL中使用glVertex函数选择单个端点的坐标位置。 glBegin(GL_POINTS): glVertex2i(); glVertex2i(); glVertex2i(); glVertex2i(); glEnd(); 世界坐标系中描述的图形部分最终要映射到输出设备的坐标系统中,图中的几 何信息被扫描转换到像素位置。下一节将介绍实现OpenGL画线函数的扫描转换 算法。 下面的OpenGL程序按三个过程组织。将所有初始化和有关的一次性设定参 数的函数放在过程init中;要显示图形的几何描述放在过程lineSegment中,该过程

·28· 机械CAD技术 将由GLUT函数glutDisplayFunc调用:Main过程包含设定显示窃口及将线段送到 屏幕的GLUT函数。图2-1所示显示窗口即为由该程序生成的红色线段。 可☒ 国21显示窗口和由示例程序生成的线段 include <GL/glut.h> void init (void) glClearColor(1.0,1.0,1.0,0.0): //将显示窗口背景设置为白色 glMatrixMode(GL_PROJECTION): /设置投影参数 glutOrtho2D(0.0,200.0,0.0,150.0); void lineSegment (void) glClear(GL._COLOR_BUFFER_BIT);//清屏 gIColor3f(1.0,0.0,0.0); //设置颜色 glBegin (GL_LINES); /指定输出图元为线段 glVertex2i(180,15); /线段的起点 glVertex2i(10,145); /线段的终点 glEnd(); glFlush(); /1刷新 void main(int argc,char**argv) glutInit (&arge,argv): /设置初始化参数
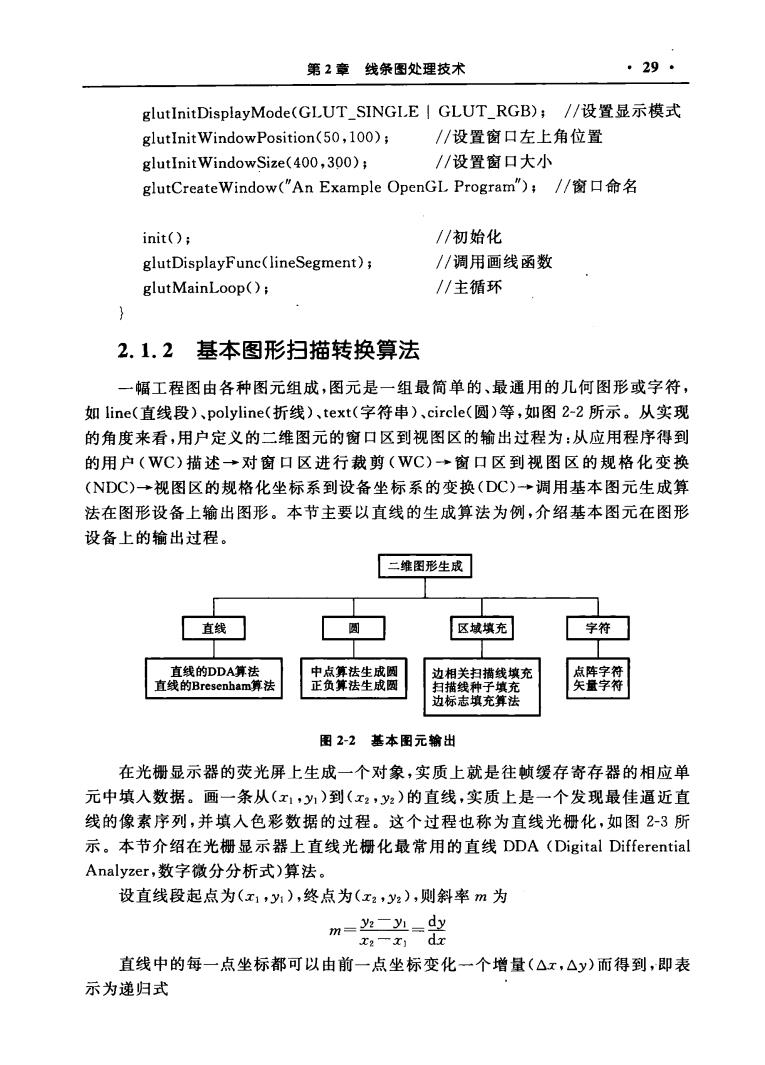
第2章线条图处理技术 ·29. glutInitDisplayMode(GLUT_SINGLE I GLUT_RGB);/设置显示模式 glutInit WindowPosition(50,100); //设置窗口左上角位置 glutInit WindowSize(400,300); /设置窗口大小 glutCreate Window("An Example OpenGL Program")/窗口命名 init(); /初始化 glutDisplayFunc(lineSegment); /调用画线函数 glutMainLoop(); /主循环 2.1.2基本图形扫描转换算法 一幅工程图由各种图元组成,图元是一组最简单的、最通用的几何图形或字符 如line(直线段)、polyline(折线)、text(字符串)、eircle(圆)等,如图2-2所示。从实现 的角度来看,用户定义的二维图元的窗口区到视图区的输出过程为:从应用程序得到 的用户(WC)描述→对窗口区进行裁剪(WC)→窗口区到视图区的规格化变换 (NDC)→视图区的规格化坐标系到设备坐标系的变换(DC)→调用基本图元生成算 法在图形设备上输出图形。本节主要以直线的生成算法为例,介绍基本图元在图形 设备上的输出过程。 二蝶图形生成 直线 区域填充 学符门 出资鞋生设圆 边相关扫描线填充 宾营子殊 边标志填充算法 图2-2基本图元输出 在光栅显示器的荧光屏上生成一个对象,实质上就是往帧缓存寄存器的相应单 元中填入数据。画一条从(x1,y)到(x2,2)的直线,实质上是一个发现最佳逼近直 线的像素序列,并填人色彩数据的过程。这个过程也称为直线光栅化,如图2-3所 示。本节介绍在光栅显示器上直线光栅化最常用的直线DDA(Digital Differential Analyzer,数字微分分析式)算法。 设直线段起点为(x1,y),终点为(x2,y2),则斜率m为 直线中的每一点坐标都可以由前一点坐标变化一个增量(△x,△y)而得到,即表 示为递归式

·30 机械CAD技术 ∫x1+1=x4十△x y4+1=y:+△y 并有关系:△y=m·△x 递归式的初值为直线的起点(x1,y),这 样,就可以用加法来生成一条直线。具体方 法是: (1)当|dx|>|dy时, |△x|=1, |△yl=m 图2-3直线和圆的生成原理 否则, △x=1/m,1△yl=1 (2)△x,△y的符号与dx,dy的符号相同。 这两条规律可以导致程序的简化。由上述方法写成的程序如下。其中stps变 量的设置,以及△x=dx/steps;△y=dy/steps等语句,正是利用了上述两条规律,使 得程序变得简练。使用DDA算法,每生成一条直线做两次除法,每画线中一点做两 次加法。因此,用DDA法生成直线的速度是相当快的, #include <stdlib.h> #include <math.h inline int round (const float a )(return int (a +0.5)) dda_line (xa,ya,xb,yb,c) int xa,ya.xb,yb.c: float delta_x,delta_y,x,y; int dx,dy,steps,k; dx=xb-xa; dy=yb-ya; if (abs(dx)>abs(dy))steps=abs(dx); else steps=abs (dy): delta_x=(float)dx /(float)steps; delta_y=(float)dy/(float)steps; x=xa: y=ya: set_pixel(round(x),round(y),c); for (k=1;k<=steps;k++)

第2章线条图处理技术 ·31 x+=delta_x; y+=delta_yr set_pixel(round(x),round(y),c); 2.2图形几何变换 2.1节介绍了如何应用基本图元来描述场景,并给出了直线段的扫描转换算法 可以将图元显示在光橱设备上。现在再看看可用于对象重定位或改变大小的操作】 在机械设计过程中,用户经常希望改变图形的比例,以便清晰地观察设计中的细 节:有时希望通过旋转图形,以便从不同角度观察对象:有时希望将图形平移到另 位置,以便在不同环境中显示对象;对于装配体的动态运动而言,在每一运动中需要 不同的平移和转动。上述在方位和比例上的变化通过图形变换实现,图形变换一般 是指将图形的几何信息经过儿何变换后产生新的图形。应用于对象几何描述并改变 它的位置、方向或大小的操作称为几何变换(geometric transformation)。图形变换 既可以看作是图形不动而坐标系变动,变动后该图形在新的坐标系下具有新的坐标 值,也可以看作是坐标系不动而图形变动,变动后的图形在坐标系中的坐标值发生 变化。 基本的几何变换研究物体坐标在直角坐标系统内的平移、旋转和变比的规律,按 照坐标的维数不同,基本变换可分为二维几何变换和三维几何变换两大类。对于线 框图形的变换,通常是以点变换为基础,把图形的一系列顶点作几何变换后,连接新 的顶点序列即可产生变换后的新图形。但对于可用参数表示的曲线、曲面等图形的 变换,基于效率的考虑,一般通过对其参数方程作变换来实现对整个图形的变换,而 不是逐点进行,这里主要介绍二维和三维线条图的几何变换 2.2.1二维图形几何变换 1.基本变换 l)平移(translation) 通过将位移量加到一个点的坐标上来生成一个新的坐标,可以实现该点的一次 平移。类似地,对于一个用多个坐标位置定义的对象,可以通过对所有坐标位置使用 相同的位移量沿平行路径重定位来实现平移,然后在新位置显示完整的对象。 将平移距离(translation distance)t,、,加到原始坐标(x,y)上获得一个新的坐 标位置(x',y),可以实现一个二维位置的平移,如图24所示。 (z'=x+t, y'=y+t