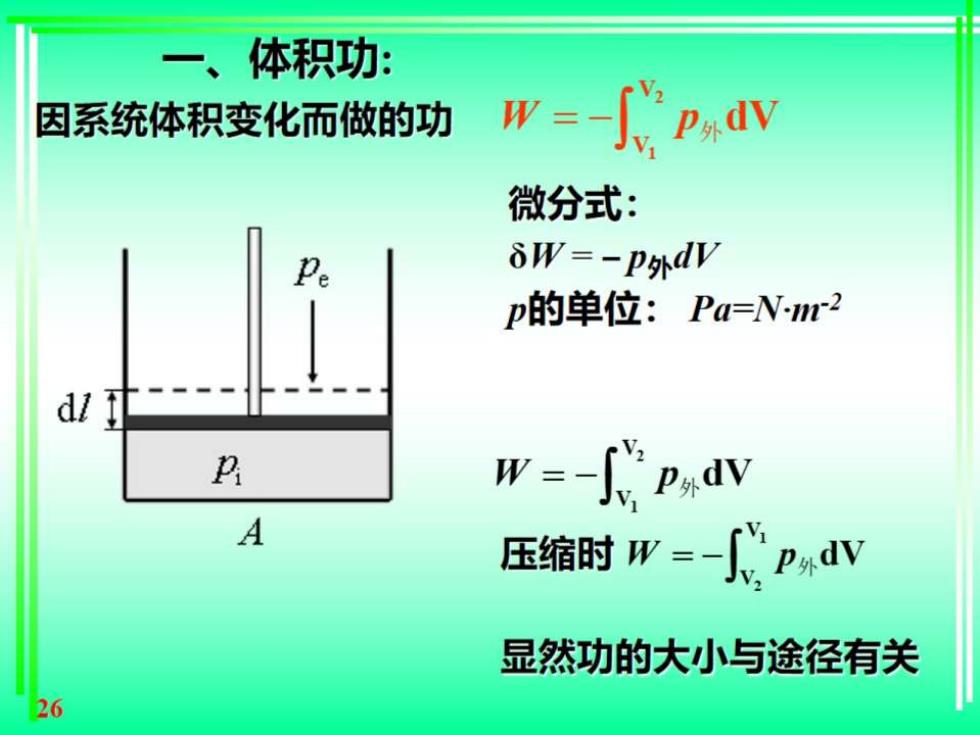
一、体积功: 因系统体积变化而做的功 w=-心p, 微分式: Pe δW=-p外dV p的单位:Pa=Nm2 dl P w=-心p,dV A 压缩时W=-心pdW 显然功的大小与途径有关 26

设在定温下,一定量理想气体在活塞筒中克 服外压P,经4种不同途径,体积从V1膨胀到 V2所作的功。 (1)向真空自由膨胀: P。=0 W=0 27
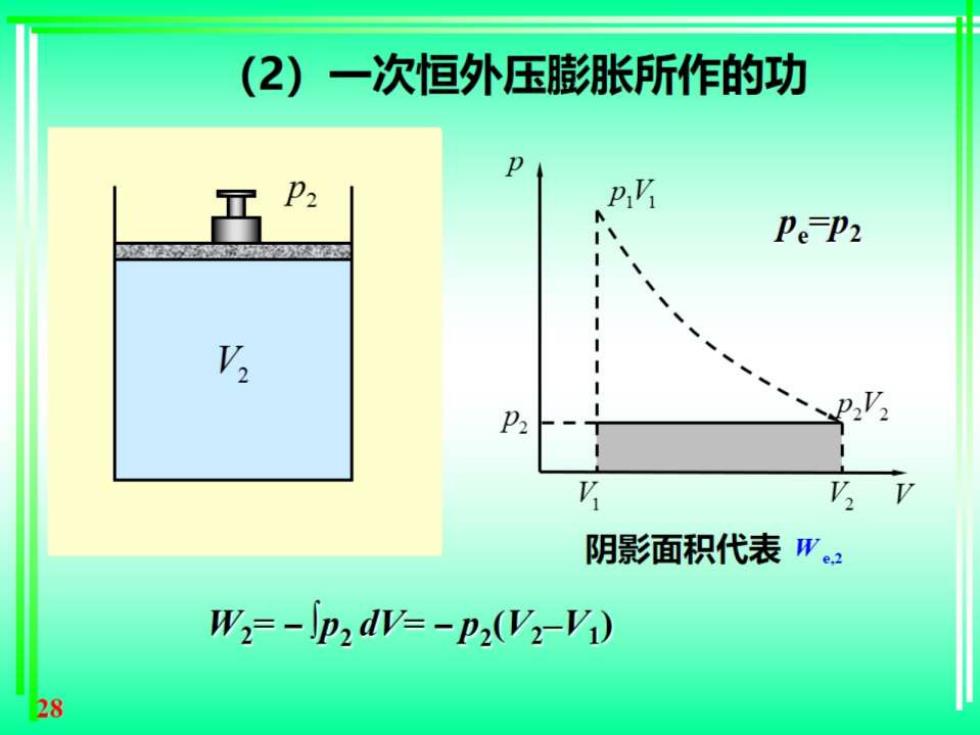
(2)一次恒外压膨胀所作的功 P2 p乃 Pe-P2 P 阴影面积代表W。2 W2=-lp2dV=-P2(V2-Vi) 28
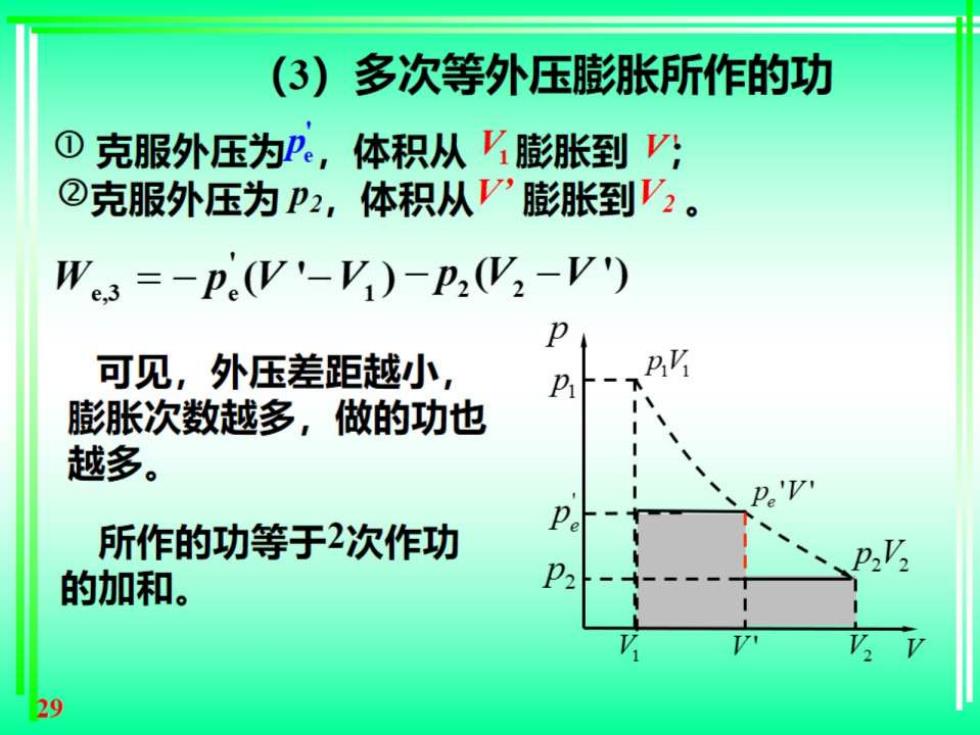
(3) 多次等外压膨胀所作的功 ①克服外压为P, 体积从膨胀到? @克服外压为P2,体积从V”膨胀到V,。 We3=-P(W'-V)-P2(V2-V') 可见,外压差距越小, p 膨胀次数越多,做的功也 越多。 所作的功等于2次作功 的加和。 29
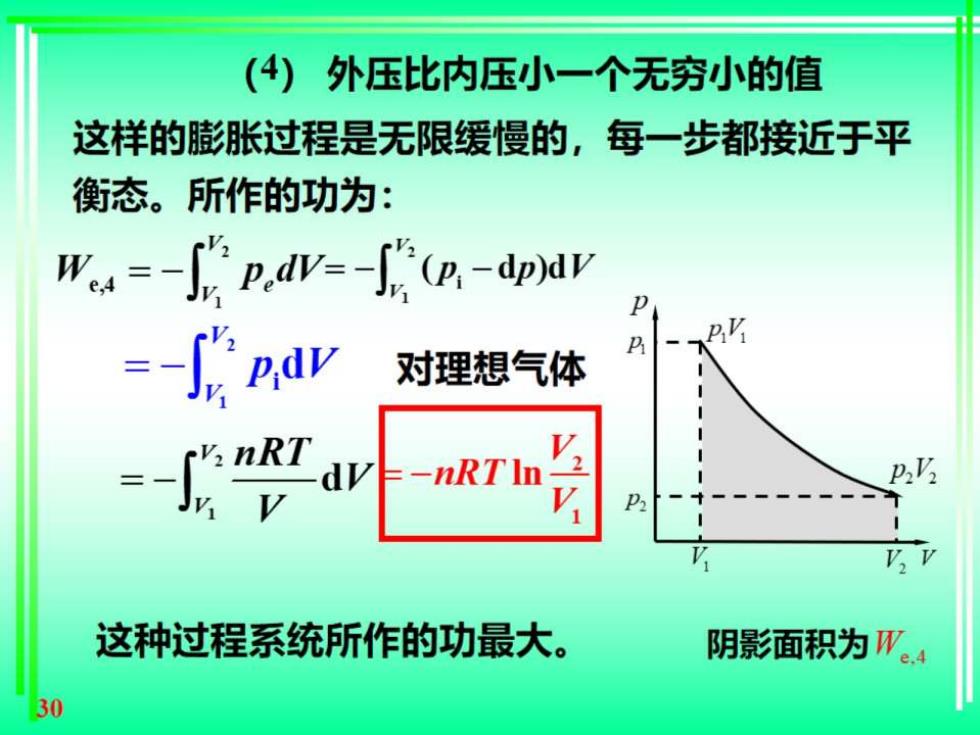
(4)外压比内压小一个无穷小的值 这样的膨胀过程是无限缓慢的,每一步都接近于平 衡态。所作的功为: W.=-fr p.dv-r (p.-dpnav =-Jpd业 对理想气体 av-nT 这种过程系统所作的功最大。 阴影面积为W。4 30