
(2)一致性 若随着样本容量n的增大,估计量的值越来越接 近于被估计的参数,则该估计量称为一致估计量。 换句话说,若当n→oo时,P(0-0k8)→1, 则0为的一致估计量。 例如:0=X就是的一致估计量 n3>n2>n1 ny n→o时,X-→u E(X)=u
(2) 一致性 若随着样本容量n的增大,估计量的值越来越接 近于被估计的参数,则该估计量称为一致估计量。 → (| − | ) →1, 换句话说,若当n 时,P 则 为的一致估计量。 例如: = X就是的一致估计量 n3n2n1 n → 时,X → X E(X) = n1 n2 n3
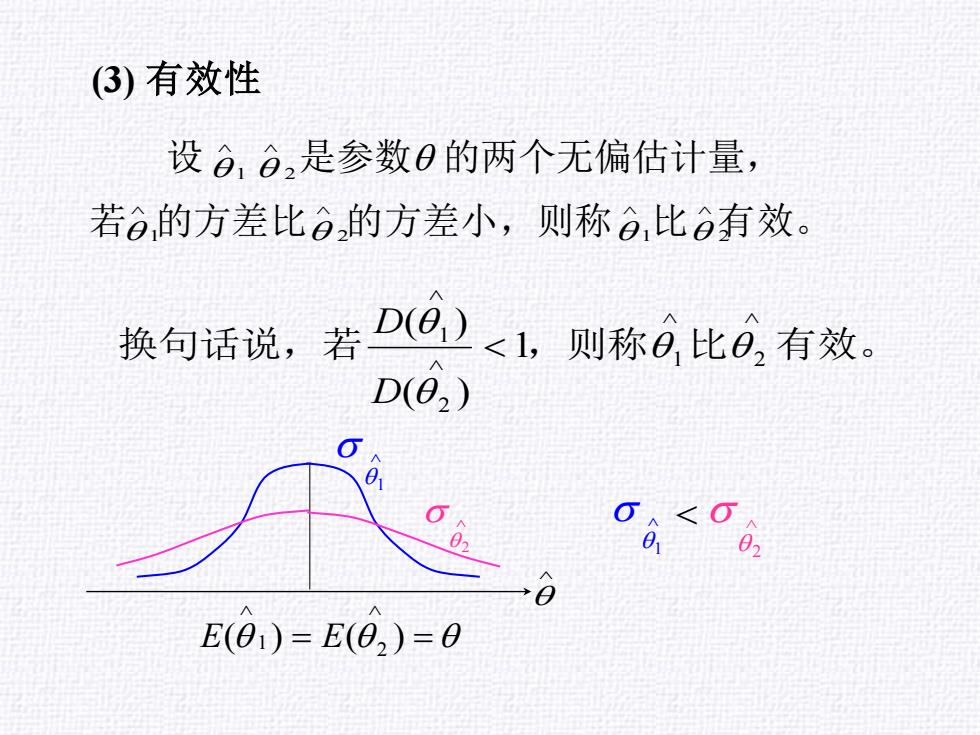
(3)有效性 设,合,是参数0的两个无偏估计量, 若合的方差比日,的方差小,则称6比合有效。 换句话说,若D)<1,则称日比日,有效。 D(02) 02 下 02 E(01)=E(02)=0
(3) 有效性 换句话说,若 ,则称 比 有效。 1 2 2 1 1 ( ) ( ) D D 设 是参数 的两个无偏估计量, 若 的方差比 的方差小,则称 比 有效。 1 2 1 2 2 1 = = ( ) ( ) 2 E 1 E 2 1 1 < 2

4.几种总体参数的点估计量 总体平均数“的点仙计至:业-了-】三名 可以证明是的无偏、一致、有效的估计量。 a体标准若的点备计长:0=s-2化-万 (3)总体成数P的点估计量:P=p
4. 几种总体参数的点估计量 = = = n Xi n X i 1 1 (1)总体平均数的点估计量: 可以证明X是的无偏、一致、有效的估计量。 = − − = = n X X n s i 1 2 i ( ) 1 1 (2)总体标准差的点估计量: P P = p (3)总体成数 的点估计量:

例:某公司考虑购买一批减价商品,这批商品 共2000件,其中有些是次品,但不知次品量或 次品率是多少。公司得知每件次品的修复成本 为0.25元,并认为若总的修复成本低于50元,购 买这批商品是有利可图的。在决定前,公司抽 取100件商品进行调查,发现12件次品。问你估 计这批商品的次品率为多少?你认为公司是否 可购买这一批商品?
例:某公司考虑购买一批减价商品,这批商品 共2000件,其中有些是次品,但不知次品量或 次品率是多少。公司得知每件次品的修复成本 为0.25元,并认为若总的修复成本低于50元,购 买这批商品是有利可图的。在决定前,公司抽 取100件商品进行调查,发现12件次品。问你估 计这批商品的次品率为多少?你认为公司是否 可购买这一批商品?

解:设样本次品率为p,则总体中的次品量为NP,即 P=p=6-12-12% n100 WP=2000×12%=240(件) 计算结果表明:该批商品估计的次品率为 12%,次品量为240件,所以该品商品的修复成 本为:240×0.25=60(元)。由此可见,公司不能购 买这批商品
解:设样本次品率为p, 则总体中的次品量为NP, 即 12% 100 12 = = = = n k P p = 200012%=240 (件) N P 计算结果表明:该批商品估计的次品率为 12%,次品量为240件,所以该品商品的修复成 本为:2400.25=60(元)。由此可见,公司不能购 买这批商品