过冷度与形核率 金属材料形核率 与温度的关系 4G*+4G 形核率突然增大 ~0.2Tm 的温度称为有效 形核温度,对应 的过冷度称临界 有效成过冷度约等于 核温度0.2Tm AT 温度一 (a) (b) 形核率与过冷度的关系 Nae-V(ar)2 N=K exp AG 16πo316πo3T7 k kT 34G2 3(Lw4T24T2 形核率随过冷度增大而增大,超过极大值后,形核率又 逢康大婆诊塞洪娄增李耍玻小
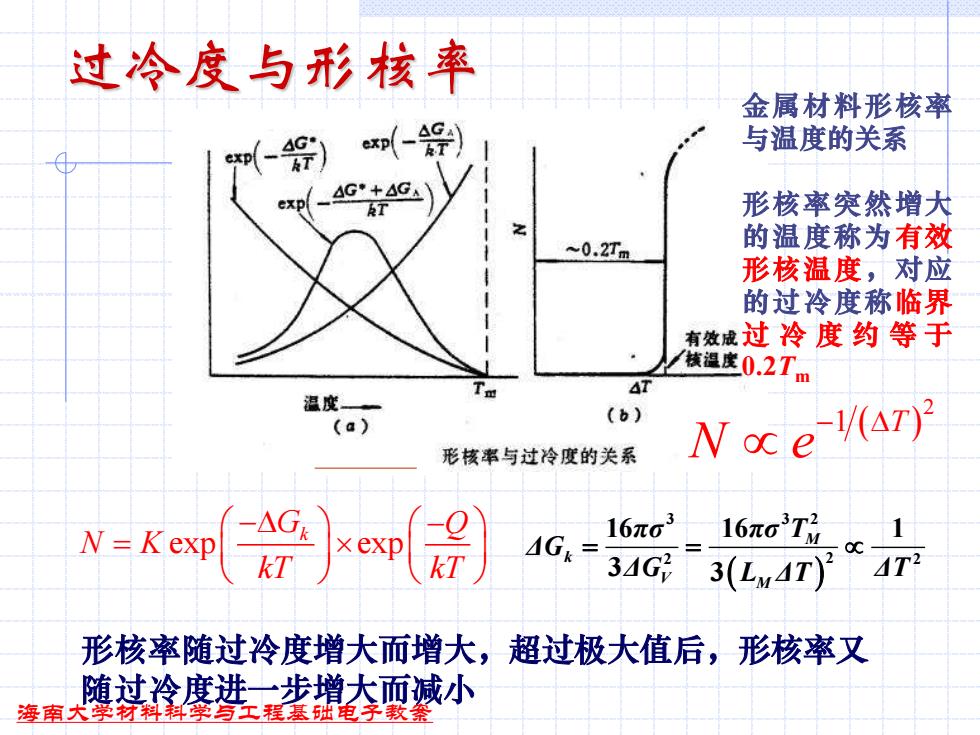
海南大学材料科学与工程基础电子教案 过冷度与形核率 ( ) M k V M πσ πσ T ΔG ΔG L ΔT ΔT = = 3 3 2 2 2 2 16 1 16 3 3 exp exp Gk Q N K kT kT − − = ( ) 2 1 T N e− 形核率随过冷度增大而增大,超过极大值后,形核率又 随过冷度进一步增大而减小 金属材料形核率 与温度的关系 形核率突然增大 的温度称为有效 形核温度,对应 的过冷度称临界 过 冷 度 约 等 于 0.2Tm

◆已知纯铜的凝固点为1085℃,熔化潜热为1628J/cm3,单 位表面能为1.77×105J/cm2,均匀形核过冷度△T=0.2Tm ,试求其在均匀形核条件下,球形晶核的临界半径。 海南大学材料科学与工程基础电子教案 22
海南大学材料科学与工程基础电子教案 22 已知纯铜的凝固点为1085℃,熔化潜热为1628J/cm3 ,单 位表面能为1.77×10-5J/cm2 ,均匀形核过冷度ΔT=0.2Tm ,试求其在均匀形核条件下,球形晶核的临界半径

例:已知纯铜的凝固点为1085℃,熔化潜热为1628J/cm3,单 位表面能为1.77X105J/cm2,均匀形核过冷度△T=0.2Tm,试 求其在均匀形核条件下,球形晶核的临界半径。 解: 根据临界晶核半径的计算公式: 2cT ,2×1.77×10-5×1358 =1.087×10-7cm △H△T 1628×0.2×1358 海南大学材料科学与工程基础电子教案 23
海南大学材料科学与工程基础电子教案 23 解: 根据临界晶核半径的计算公式: 例:已知纯铜的凝固点为1085℃,熔化潜热为1628J/cm3 ,单 位表面能为1.77×10-5J/cm2 ,均匀形核过冷度ΔT=0.2Tm,试 求其在均匀形核条件下,球形晶核的临界半径。 * σT m . r . cm H T . 5 2 2 1 77 10 1358 7 1 087 10 Δ Δ 1628 0 2 1358 − − = = =

例:考虑在一个大气压下液态铝的凝固,对于不同程度的过冷 度,即:△T=1,10,100和200℃,计算: (a)临界晶核尺寸; b)从液态转变到固态时,单位体积的自由能变化△G° (形核功); (c)从液态转变到固态时,临界尺寸广处的自由能的变化△G,。 (铝的熔点Tm=993K,单位体积熔化热Lm=1.836×10J/m3,固 液界面比表面能o=93mJ/m) 海南大学材料科学与工程基础电子教案 24
海南大学材料科学与工程基础电子教案 24 例:考虑在一个大气压下液态铝的凝固,对于不同程度的过冷 度,即:ΔT=1,10,100和200℃,计算: (a) 临界晶核尺寸; (b) 从液态转变到固态时,单位体积的自由能变化ΔG* (形核功); (c) 从液态转变到固态时,临界尺寸r *处的自由能的变化ΔGv。 (铝的熔点Tm=993K,单位体积熔化热Lm=1.836×109J/m3,固 液界面比表面能σ=93mJ/m2 )

解: 20Ts (a)·临界晶核尺寸r=Lw△T 因为△T=.T.-T是正值,所以x为正,将过冷度△T=1℃代入,得: 2×93×103J1m2×933K 1.836×10°J1%×1K =9.45×10-8m=94.5am(945A -L△7-1836×109J1m×1K.-1.97×106J1m2 (b) G Tw 933K
海南大学材料科学与工程基础电子教案 25 (b)