《线性代数》课程PPT教学课件（同济第五版）第二章 矩阵及其运算 第二节 矩阵的运算

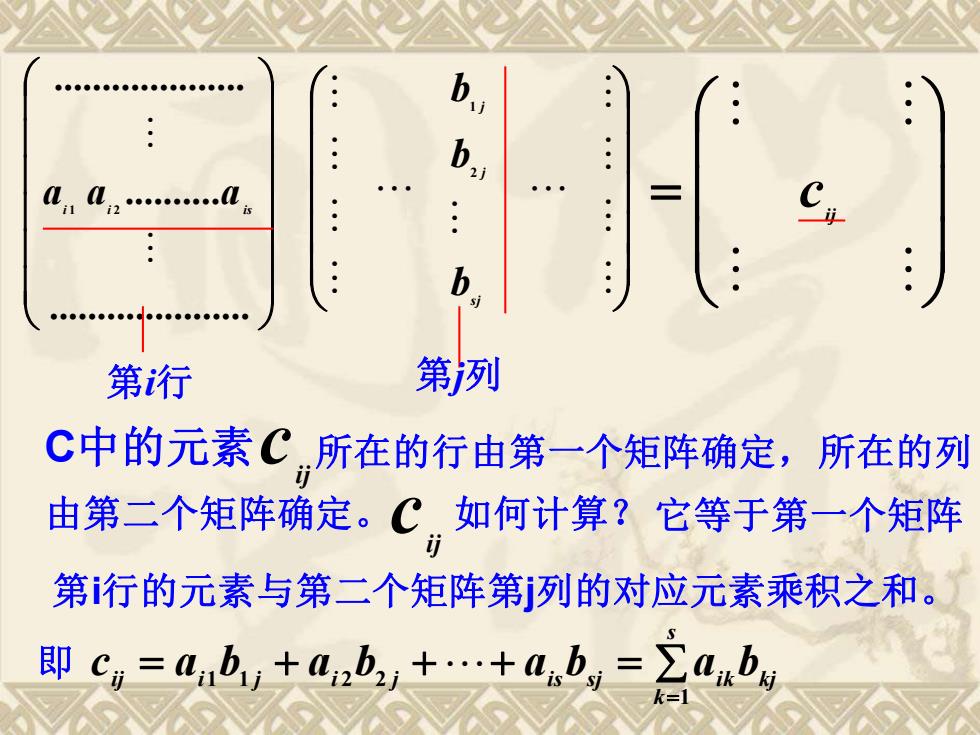
b b., aa. b 第行 第冽 C中的元素C所在的行由第一个矩阵确定，所在的列 由第二个矩阵确定。C如何计算？它等于第一个矩阵 第行的元素与第二个矩阵第j列的对应元素乘积之和。 即c=by+ab2+.+ab,=ab

                . . . 1 2   ai ai ais                          s j j j b b b 2 1           =     ij c 第i行 第j列 C中的元素 ij c 所在的行由第一个矩阵确定， 由第二个矩阵确定。 所在的列 如何计算？ ij c 它等于第一个矩阵 第i行的元素与第二个矩阵第j列的对应元素乘积之和。 即 = + + + =  = s k i j i j i j i s sj i k kj c a b a b a b a b 1 1 1 2 2 

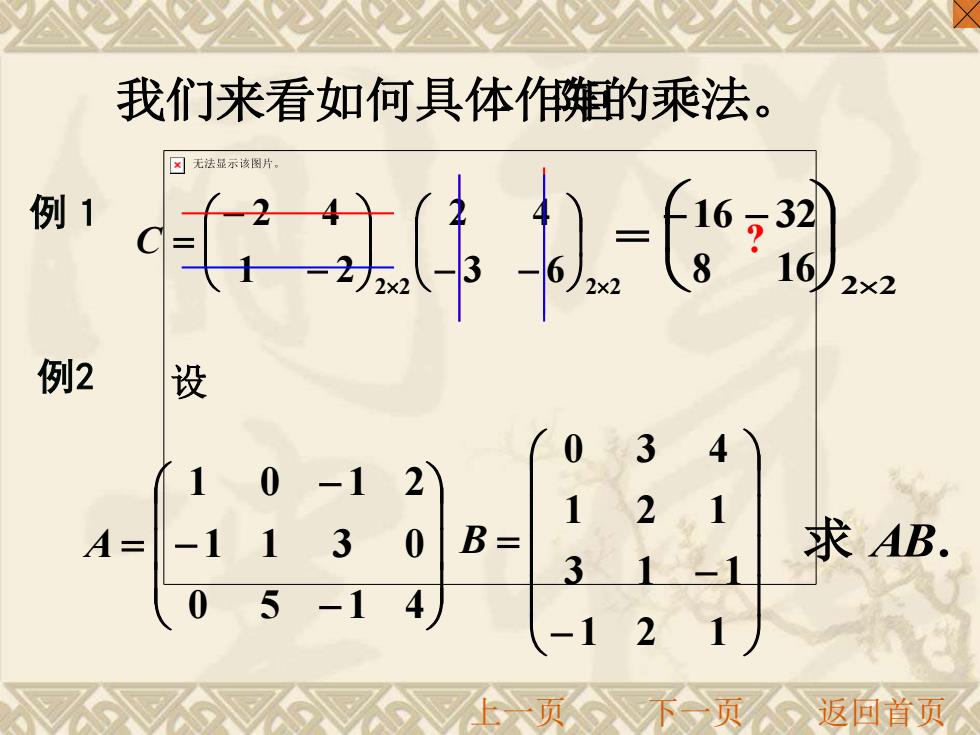
我们来看如何具体潍的乘法。 ☒无法显示该图 例1 16 2×2 例2 设 0 3 4 1 0 2 1 2 1 A= -1 1 3 0 B= 求AB. 3 -1 0 5 -1 4 -1 2 下页返间首页

例１ 2 2 2 2 3 6 2 4 1 2 2 4         − −       − − C = 22       = −16 − 32 8 16 设           − − − = 0 5 1 4 1 1 3 0 1 0 1 2 A             − − = 1 2 1 3 1 1 1 2 1 0 3 4 B 例2 ? 上一页 下一页 返回首页 我们来看如何具体作矩阵的乘法。求 AB

解 A=(ag)B=(b)3 i.C=(ei)s 故 (上= C=AB= 05=十4 -5 6 102 -6 -21710 上一页G入不页返向首页

故             − −           − − − = = 1 2 1 3 1 1 1 2 1 0 3 4 0 5 1 4 1 1 3 0 1 0 1 2 C AB .           = 解 ( ) , 34  A = aij ( ) 43, B = bij ( ) . 33  = ij C c − 5 6 7 10 2 − 6 − 2 17 10 上一页 下一页 返回首页

大家想一想下面的矩阵乘法可 作吗？为什么？等于什么？ =(1×3+2×2+3×1)=(10), 入上页不页返首项

大家想一想下面的矩阵乘法可 作吗？为什么？等于什么？ ( )           1 2 3 1 2 3 = (1 3 + 2 2 + 31) = (10). 上一页 下一页 返回首页

-2 4 伽 设A= 24 求AB与BA. ☒无法显示图片1 -2 3 解 以360 AB BA= 30 说明()由缈知AB有意义而BA却没有意」 由那知AB和BA都有意义，但4B≠BA

说明（1）         − − =         − − = 3 6 2 4 , 1 2 2 4 设A B 求AB与BA. 解         − − =        − −         − − = 8 16 16 32 3 6 2 4 1 2 2 4 AB . 0 0 0 0 1 2 2 4 3 6 2 4         =        − −         − − BA = 由例2知AB有意义而BA却没有意义。 由例3知AB和BA都有意义，但AB  BA. 例3