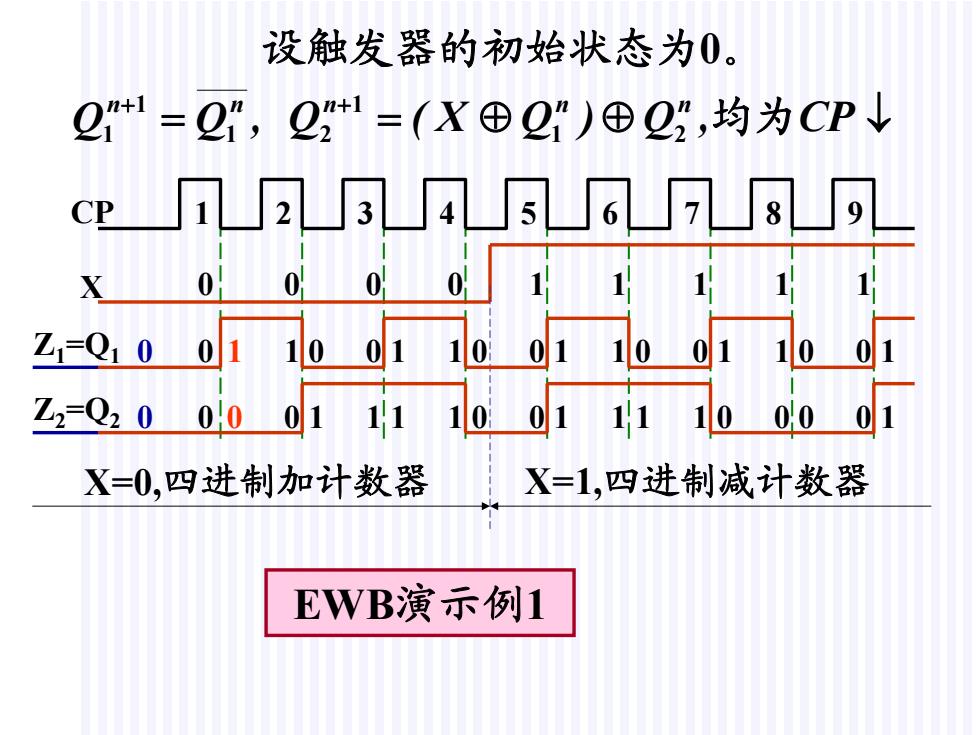
设触发器的初始状态为0。 21=2,221=(X⊕2")⊕22,均为CP↓ cpT2J34567J89 00 0 0 1出 11 ZQ10011001100110011001 Z2=Q20 000111100111100001 X=0,四进制加计数器 X=1,四进制减计数器 EWB演示例1
CP 1 2 3 4 5 6 7 8 9 X Z1 =Q1 Z2 =Q2 0 0 1 1 0 0 0 1 0 0 1 1 X=0,四进制加计数器 X=1,四进制减计数器 0 0 0 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 0 1 0 0 1 1 1 1 1 0 1 1 0 1 1 0 QQ , n n1 1 1 CP,Q)QX(Q2n 1 1n 2n 均为 设触发器的初始状态为0。 EWB演示例1
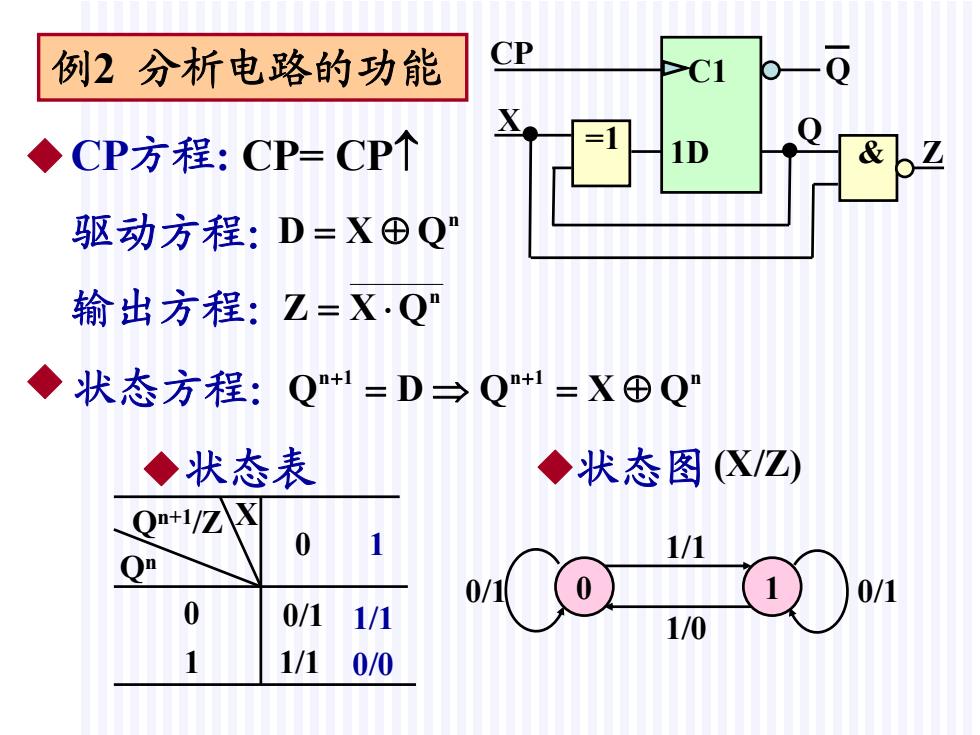
例2分析电路的功能 CP -C1 X ◆CP方程:CP=CP个 驱动方程:D=X⊕Q" 输出方程:Z=XQ" ◆状态方程:Q+1=D→Q1=X田Q” ◆状态表 ◆状态图X/Z) Q+1/Z 0 1/1 0/1 0/1 0 0/11/1 1/0 1/10/0
例2 分析电路的功能 =1 • • & CP X Q Q 1D Z C1 驱动方程: n QXD 输出方程: n QXZ 0 1 0/1 1/1 0/1 0/1 1/1 1/0 1/1 0/0 ◆CP方程: CP= CP 状态方程: 1n 1n n QXQDQ ◆ 0 1 X Qn Qn+1/Z ◆状态表 0 1 ◆状态图(X/Z)

CP方程:CP=CP个 EWB演示例2 输出方程:Z=XQ” 状态方程:Q+1=D→Q1=X⊕Q" ◆时序图:设初初始状态Q=0,则Z=1。 T23456789 功能:X连续输入两个1时,Z=0,并返回初态
输出方程: n QXZ CP方程: CP= CP 状态方程: 1n 1n n QXQDQ ◆时序图: 设初初始状态Q=0,则Z=1。 CP 1 2 3 4 5 6 7 8 9 X 0 1 1 1 0 1 1 0 1 0 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 0 Q Z 0 1 功能: X连续输入两个1时, Z=0, 并返回初态. EWB演示例2

6.2 Sequential Circuits Analysis Method 分析时序逻辑电路的一般步骤 1.由给定的时序电路写出:各FF的时钟方程和 驱动方程,时序电路的输出方程。 2.将驱动方程代入相应F℉的特性方程,求得各 F℉的次态方程,即时序电路的状态方程。 3.根据状态方程和输出方程,列出该时序电路 的状态表,画出状态图或时序图。 4.由状态表/状态图或时序图说明电路的功能
6.2 Sequential Circuits Analysis Method Sequential Circuits Analysis Method 1. 由给定的时序电路写出: 各FF的时钟方程和 驱动方程,时序电路的输出方程。 2. 将驱动方程代入相应FF的特性方程, 求得各 FF的次态方程, 即时序电路的状态方程。 3. 根据状态方程和输出方程, 列出该时序电路 的状态表, 画出状态图或时序图。 4. 由状态表/状态图或时序图说明电路的功能。 一、分析时序逻辑电路的一般步骤
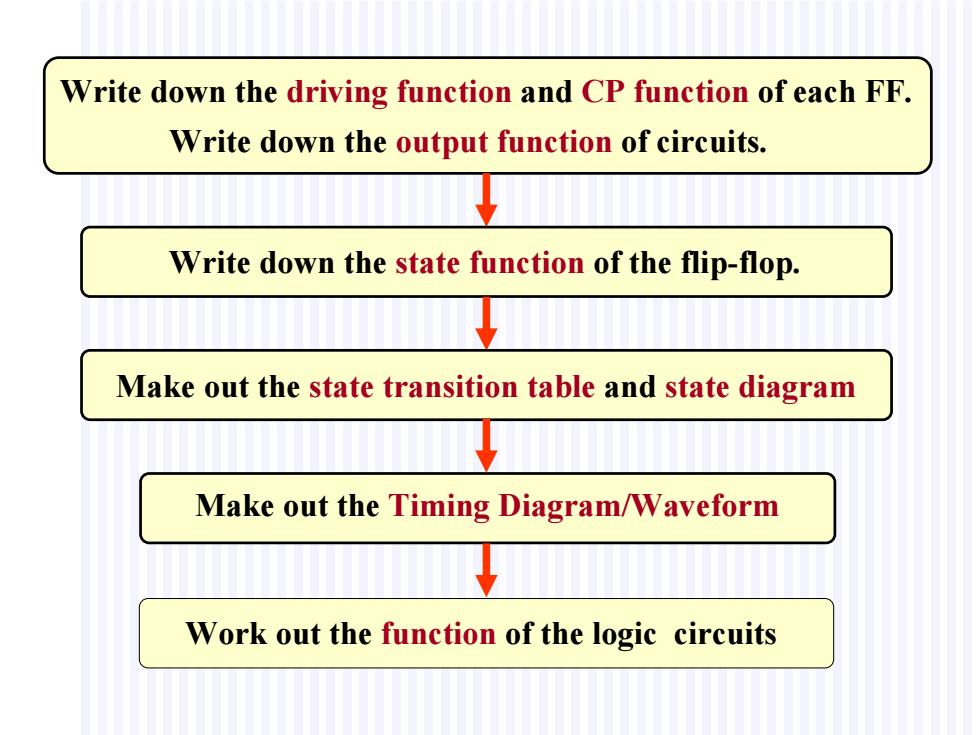
Write down the driving function and CP function of each FF. Write down the output function of circuits. Write down the state function of the flip-flop. Make out the state transition table and state diagram Make out the Timing Diagram/Waveform Work out the function of the logic circuits
Write down the driving function and CP function of each FF. Write down the output function of circuits. Write down the state function of the flip-flop. Make out the state transition table and state diagram Make out the Timing Diagram/Waveform Work out the function of the logic circuits