海南大学：《电子技术基础》课程教学课件（数字电子技术基础）06 时序逻辑电路 Sequence Logic Circuits Analysis & Design

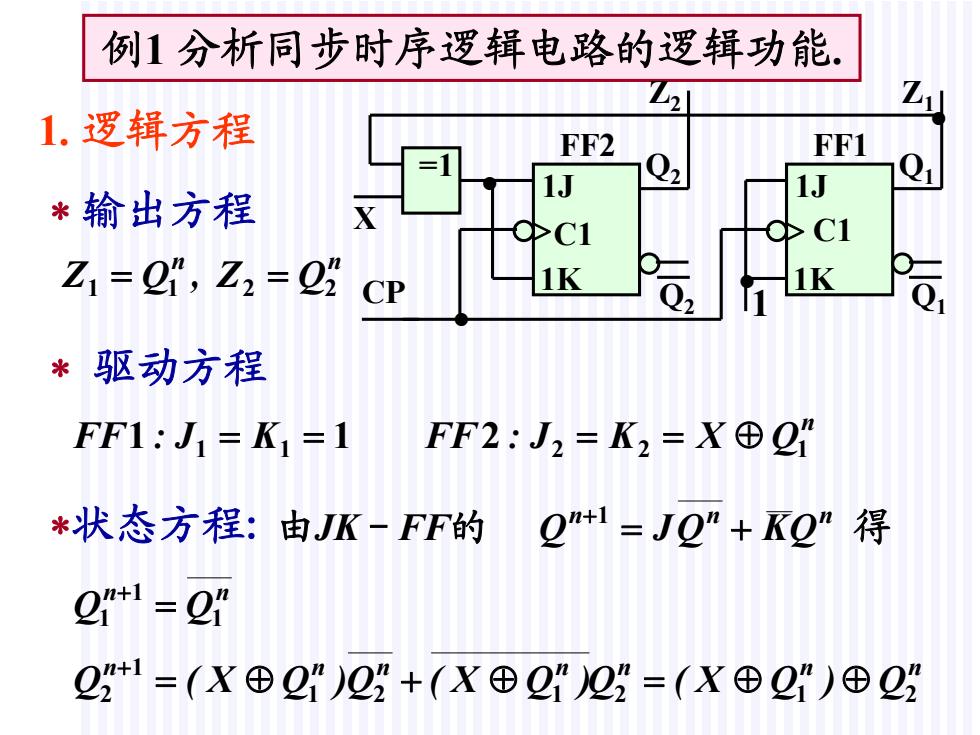
例1分析同步时序逻辑电路的逻辑功能. Z 1.逻辑方程 FF2 FF1 *输出方程 Z1=2",Z2=02 CP 1K 1K *驱动方程 FF1:J1=K1=1 FF2:J2=K2=X⊕Q” *状态方程：由JK-FF的 Q+1=JQ”+K0”得 201=2” 2+1=(X⊕2")2+(X⊕21”22=(X⊕21)⊕22

 输出方程 n n  QZ,QZ 2211  驱动方程 n KJ:FF 11 22 QXKJ:FF 1 1  2 1  状态方程: 由 的－ n1 n  QKQJQFFJK n 得 n n QQ 1 1 1   n nn nn nn 21 21 Q)QX(Q)QX(Q)QX(Q 21 1 2   例1 分析同步时序逻辑电路的逻辑功能. 1. 逻辑方程 1J 1K C1 FF2 1J 1K C1 FF1 • • • • Z2 Z1 Q2 Q1 Q2 Q1 X CP =1 1  

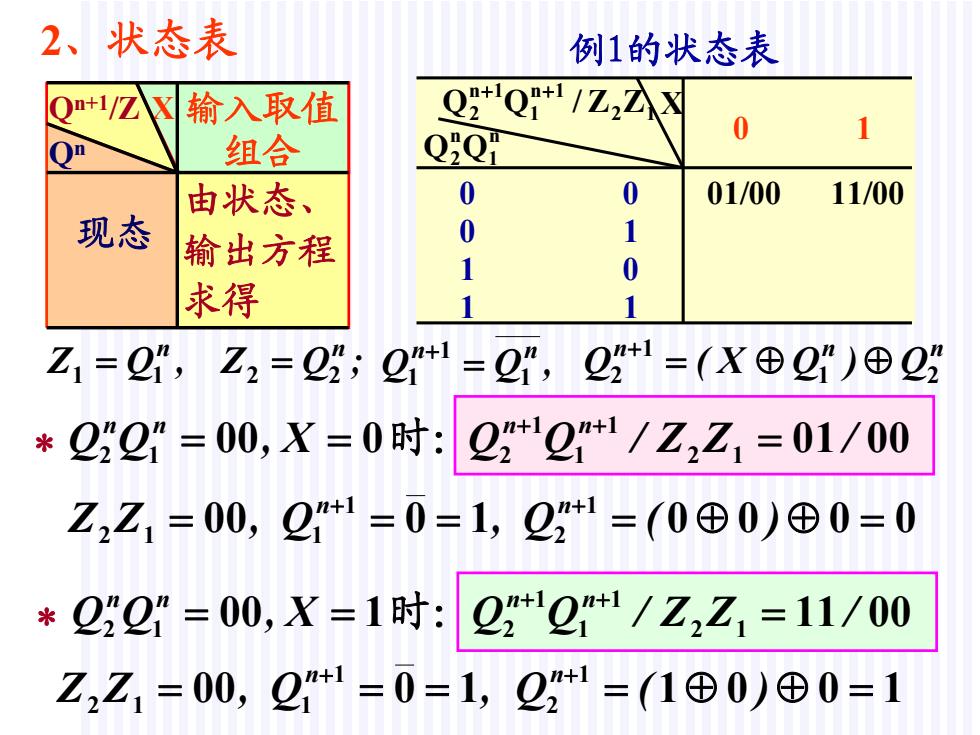
2、状态表 例1的状态表 +1/Z 输入取值 Qg*'Q+'/Z2公☒ 0 组合 Q2Q 由状态、 0 0 01/00 11/00 现态 输出方程 0 1 1 0 求得 1 1 Z1=2”,Z2=22;211=21,22+1=(X⊕2")⊕2 *22”2”=00,X=0时： 221/Z2Z1=01/00 Z2Z1=00,2+1=0=1,221=(0⊕0)⊕0=0 *222”=00,X=1时： 2221/Z2Z1=11/00 Z,Z,=00,0+1=0=1,Q21=(1⊕0)©0=1

12 X 1n1 1n2 ZZ/QQ   n 1 n 2QQ 例1的状态表 Qn+1/Z 由状态、 输出方程 求得 Qn 现态 X 输入取值 组合 0 1 0 0 0 1 1 0 1 1 2、状态表 01/00 11/00 ,QQn n1 1 1   n nn Q)QX(Q 21 1 2   ;QZ,QZ n n   2211  12 nn  X,QQ  0 00 时： Z Z 00, 12  Q , n 10 1 1    0000 1 2      )(Qn 0001 12 1 1 1 2 /ZZ/QQ nn     12 nn  X,QQ  1 00 时： Z Z 00, 12  Q , n 10 1 1    1001 1 2      )(Qn 0011 12 1 1 1 2 /ZZ/QQ nn   

21=(X⊕21")⊕2 例1的状态表 Q+'Q'/z2公X 21=21, 0 Q2QT 0 0 01/00 11/00 Z2Z1=2221", 0 1 10/01 00/01 11/10 01/10 1 00/11 10/11 *222”=01,X=0时： 221/Z2Z1=10/01 Z2Z1=01,2"1=1=0,21=(0⊕1)⊕0=1 *222”=01,X=1时： 22'21/Z2Z1=00/01 Z2Z1=01,21=1=0,221=(1⊕1)⊕0=0

12 X 1n1 1n2 ZZ/QQ   n 1 n 2QQ 例1的状态表 0 1 0 0 0 1 1 0 1 1 01/00 11/00 QQ , n n1 1 1   n n n 1 Q)QX(Q 2 1 2     ;QQZZ nn  1212  12 nn  X,QQ  0 01 时： Z Z 01, 12  Q , n 01 1 1    1010 1 2      )(Qn 0110 12 1 1 1 2 /ZZ/QQ nn     12 nn  X,QQ  1 01 时： Z Z 01, 12  Q , n 01 1 1    0011 1 2      )(Qn 0100 12 1 1 1 2 /ZZ/QQ nn    10/01 00/01 11/10 01/10 00/11 10/11

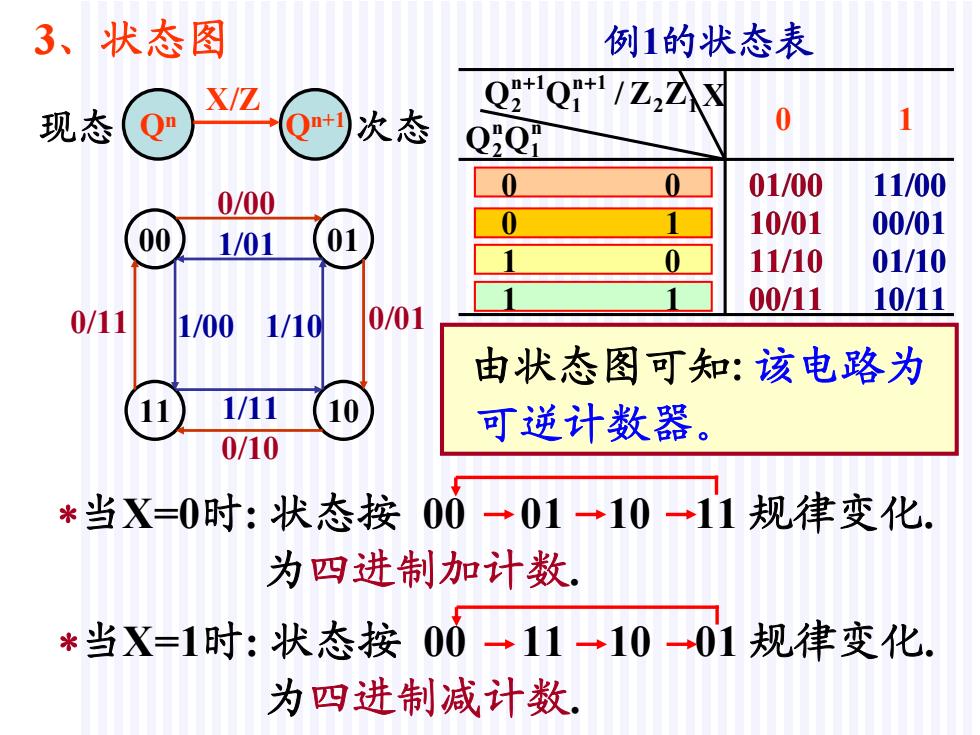
3、状态图 例1的状态表 X/Z 现态 Qn 次态 0 QZQ 0 01/00 11/00 0/00 0 00 1 10/01 00/01 1/01 0 11/10 01/10 00/11 10/11 0/11 1/00 1/10 0/01 由状态图可知：该电路为 1/11 可逆计数器。 0/10 *当X=0时：状态按00一01→10一11规律变化. 为四进制加计数。 *当X=1时：状态按00一11一10-01规律变化. 为四进制减计数

01/00 0 1 0 0 0 1 1 0 1 1 12 X 1n1 1n2 ZZ/QQ   n 1 n 2QQ 例1的状态表 10/01 11/10 00/11 11/00 00/01 01/10 10/11 00 01 11 10 01/00 3、状态图 现态 Qn Qn+1 次态 X/Z 0/00 0/01 0/10 0/11 1/00 1/11 1/10 1/01 10/01 11/10 00/11 11/00 00/01 01/10 10/11 由状态图可知:该电路为 可逆计数器。 当X=0时: 状态按 00 01 10 11 规律变化. 为四进制加计数. 当X=1时: 状态按 00 11 10 01 规律变化. 为四进制减计数

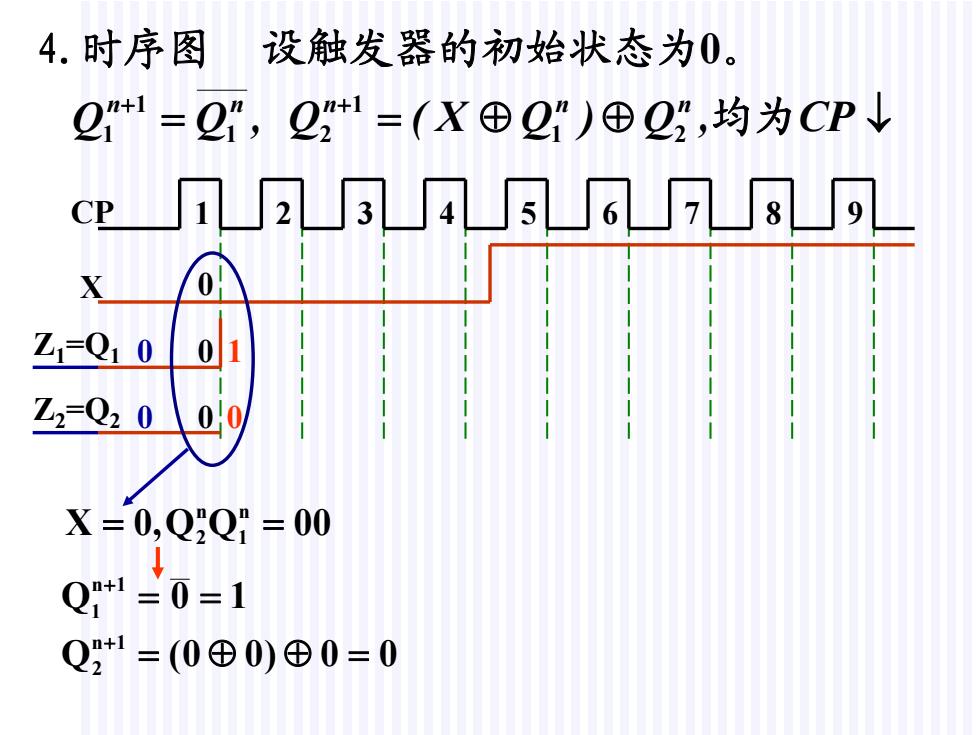
4.时序图 设触发器的初始状态为0。 21=2,221=(X⊕2")⊕22，均为CP↓ 73456789 CP Z=Q10 01 Z2-Q20 00 X=0,QQ1=00 ↓ Q*1=0=1 Q:1=(0⊕0)⊕0=0

4.时序图 CP 1 2 3 4 5 6 7 8 9 X Z1 =Q1 Z2 =Q2 0 0 0 0 0 1 0 00QQ,0X n1 n  2  00)00(Q 10Q 1n 2 1n 1      QQ , n n1 1 1        CP,Q)QX(Q2n 1 1n 2n 均为 设触发器的初始状态为0