
G是一个群? We must show that G is a group under composition of functions and find an isomorphism between G and G.We have closure under composition of functions since (Agoλh)(a)=入g(ha)=gha=入gh(a). Also, 入e(a)=ea=a and (入g-1o入g)(a)=入g-1(ga)=91ga=a=入e(a)
𝐺ҧ是一个群?
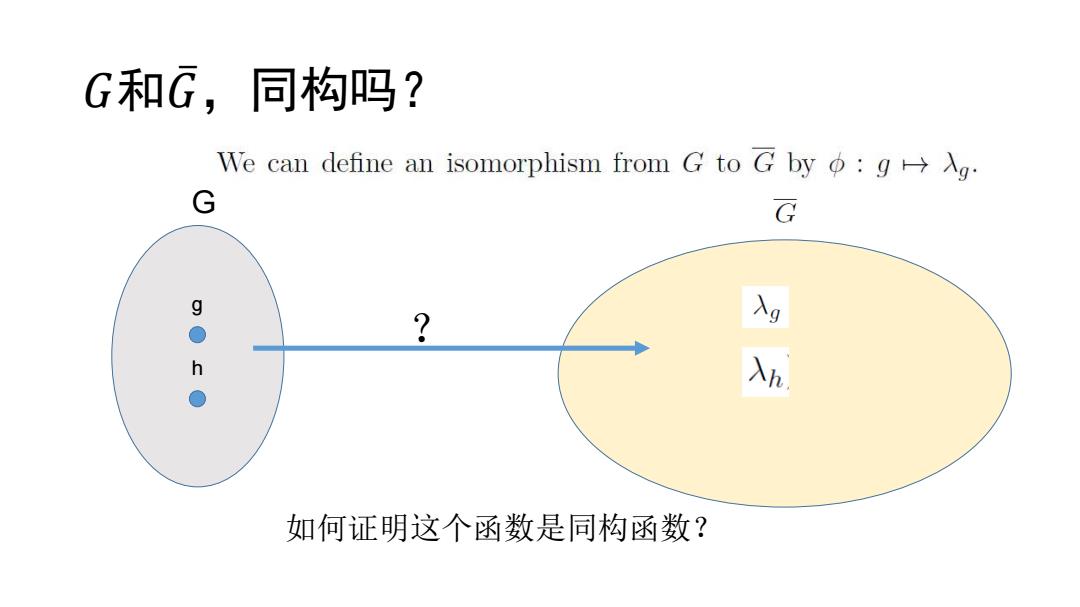
G和G,同构吗? We can define an isomorphism from G to G by:gAg G G ? h Ah 如何证明这个函数是同构函数?
𝐺和𝐺ҧ,同构吗? G g h ? 如何证明这个函数是同构函数?

G和G,同构吗? We can define an isomorphism from G to G by gAg.The group operation is preserved since (gh)=入gh=入g入h=(g)(h) It is also one-to-one,because if o(g)(a)=o(h)(a),then ga=入ga=入ha=ha. Hence,g=h.ThatΦis onto follows from the fact that(g)=λg for any Ag∈G. ▣
𝐺和𝐺ҧ,同构吗?

两个群的外直积(External Direct Product) The group Gx H is called the external direct product of G and H.Notice that there is nothing special about the fact that we have used only two groups to build a new group. The direct product ΠG=G×G2×…×Gn i=1 of the groups G1,G2,...,Gn is defined in exactly the same manner.If G =G1 G2 .·=Gn,we often write Gn instead of GI x G2×·×Gn
两个群的外直积(External Direct Product)