
问题3.1:这个定理给我们什么感觉? The isomorphism of groups determines an equivalence rela- tion on the class of all groups. 如何去证明这个定理?
问题3.1:这个定理给我们什么感觉? 如何去证明这个定理?

几个有趣的同构结论 Theorem 9.7.All cyclic groups of infinite order are isomorphic to Z. Theorem 9.8.If G is a cyclic group of order n,then G is isomorphic to Zn. Corollary 9.9.If G is a group of order p,where p is a prime number,then G is isomorphic to Zp. Theorem 9.12 Cayley.Every group is isomorphic to a group of permutations
几个有趣的同构结论

Cayley,定理的证明 Theorem 9.12 Cayley.Every group is isomorphic to a group of permutations. ·从任意一个群G出发,构造一个置换群G’: ·由置换函数组成的群 G={g:9∈G ·由G出发,构造置换函数,置换函数的个数和群G相同 入g(a)=ga. ·构造群G到置换群G’的同构函数 ·证明这个函数的双射 0:g→入g ·证明这个函数是G到G’的同构
Cayley定理的证明 • 从任意一个群G出发,构造一个置换群G’: • 由置换函数组成的群 • 由G出发,构造置换函数,置换函数的个数和群G相同 • 构造群G到置换群G’的同构函数 • 证明这个函数的双射 • 证明这个函数是G到G’的同构
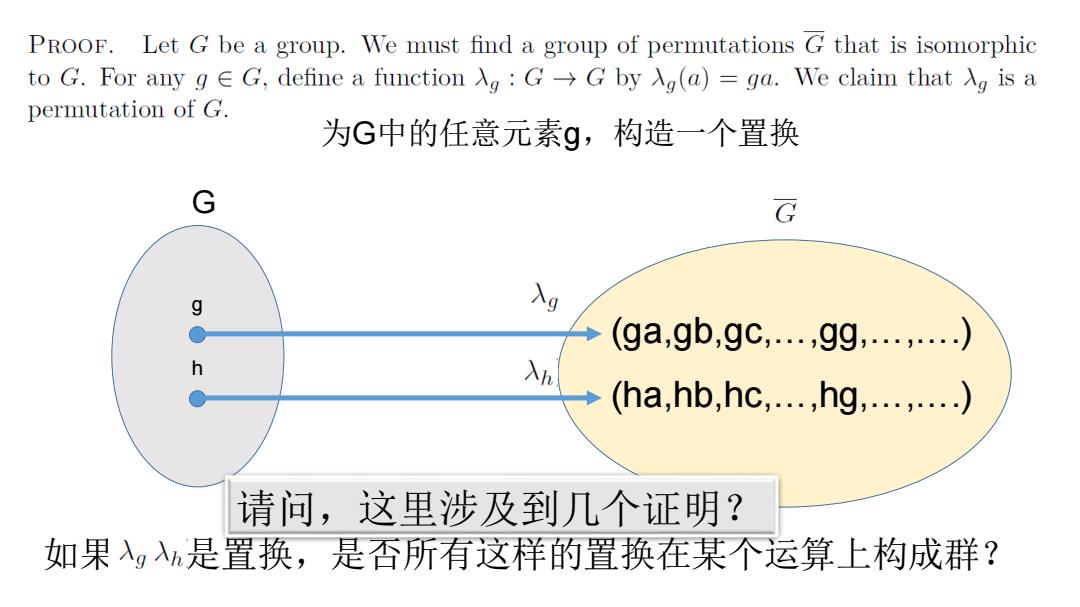
PROOF.Let G be a group.We must find a group of permutations G that is isomorphic toG.For any g∈G,define a functionλg:G→Gbyλg(a)=ga.W'e claim thatλgisa permutation of G. 为G中的任意元素g,构造一个置换 G G 入g (ga,gb,gc,…,gg,.….…) (ha,hb,hc,.,hg,.….) 请问,这里涉及到几个证明? 如果λg是置换,是否所有这样的置换在某个运算上构成群?
为G中的任意元素g,构造一个置换 G g (ga,gb,gc,…,gg,…,….) h (ha,hb,hc,…,hg,…,….) 如果 是置换,是否所有这样的置换在某个运算上构成群? 请问,这里涉及到几个证明?

2g是permutation? For any g∈G,define a function入g:G→Gby入g(a)=ga.We claim thatλgisa permutation of G.To show that Ag is one-to-one,suppose that Ag(a)=Ag(b).Then ga=入g(a)=λg(b)=gb. Hence,a =b.To show that A is onto,we must prove that for each a G,there is a b such that Ag(b)=a.Let b=g-a
𝜆𝑔 是permutation?