
4.过程W、Q、△U、△H的计算 (1)理想气体简单状态变化过程 AU-CdT-nCvdT △H=∫Cdr=n:Cndn w=jam-∫ -P.(V-V) (等外压) 0 (恒容) AU=∫C,dn(绝热) Q=AU-w-jpu=-nr哈 (定温可逆)) 6
6 4.过程W、Q、ΔU、 ΔH的计算 (1)理想气体简单状态变化过程 2 2 1 1 , T T V V m T T = = U C dT n C dT 2 2 1 1 , T T p p m T T = = H C dT n C dT W p dV = − = e 2 1 ( ) e − − p V V (等外压) 0 (恒容) U (绝热) 2 1 T V T = C dT Q = − U W 2 1 lnV pdV nRT V − = − (定温可逆)

(2)相变化过程 可逆相变 △H=n△相Hm △U=Q+W=△H-p△V w=-∫p.dw=-∫pw=-pw-) =-pV=-nRT (末态为气态,且 为理想气体) 2p=△H 不可逆相变 △U和△H可通过在始终态间设计过程计 算,W和Q必须按照实际途径计算
7 (2)相变化过程 可逆相变 = H n H相 m W e = − = − p dV pdV 2 1 = − − p V V ( ) g = − = − pV nRT (末态为气态,且 为理想气体) = + U Q W = − H p V Q H p = 不可逆相变 ΔU和ΔH可通过在始终态间设计过程计 算,W和Q必须按照实际途径计算

(3)化学变化过程 AH=5·△,H=5∑yAH)=5(-∑y△.H品) △U=5·△,UR=5A,H-∑y,RT) (定压) 2w (定容) Q=△H (定压,W'=0) Q=△U (定容,W=0)》
8 (3)化学变化过程 r m H H = ( ) B f m H = ( ) B c m H = − U Ur m = ( ) r m g H RT = − W p dV = − e ( ) g = − = − p V n RT (定压) = 0 (定容) Q H = (定压, W’=0) Q = U (定容, W’=0)
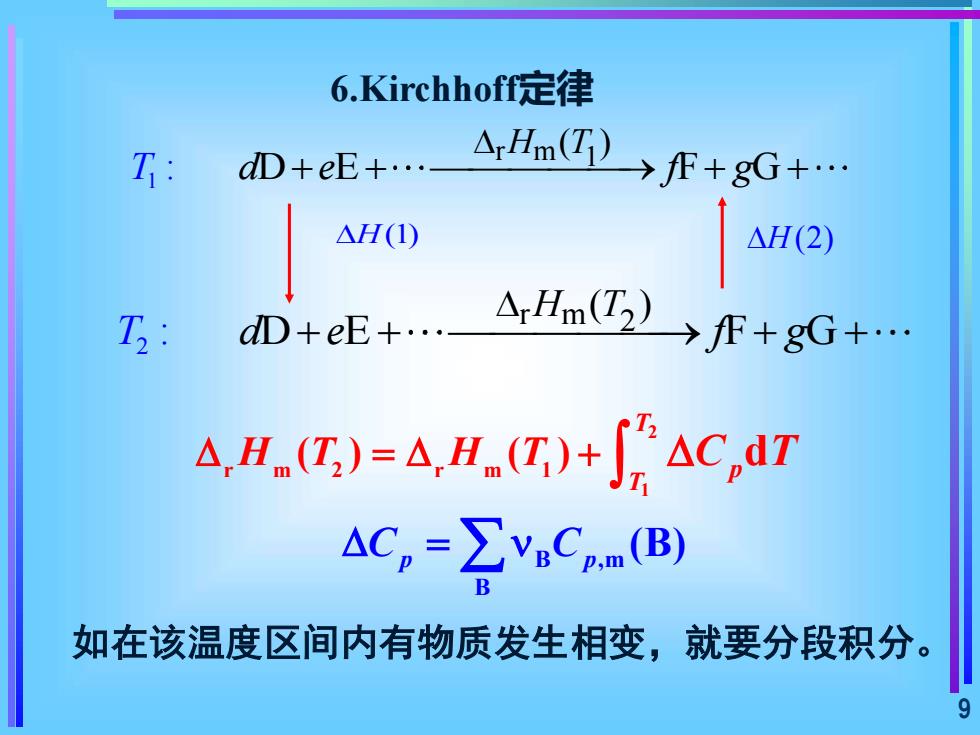
6.Kirchhoff定律 T: aD+eE+. △rHm(T) →fF+gG+ AH(D T: D+eE+ Hn )→F+gG+ △Hn(I)=△,H(T)+△C,dT ACp=∑VCnm(B) 如在该温度区间内有物质发生相变,就要分段积分。 9
9 6.Kirchhoff定律 2 1 r m 2 r m 1 ( ) ( ) d T p T = + H T H T C T B ,m B (B) = C C p p 如在该温度区间内有物质发生相变,就要分段积分。 1 r m 1 ( ) : D E F G H T T d e f g + + ⎯⎯⎯⎯⎯→ + + 2 r m 2 ( ) : D E F G H T T d e f g + + ⎯⎯⎯⎯⎯⎯→ + + H(1) H(2)

1.热机的效率 =1- _2+2=1+ T 2 2 + 2 =0 卡诺定理 所有工作于同温热源和同温冷源之间的热机, 其效率都不能超过可逆机(即卡诺热机),即可逆机 的效率最大。 7≤7R 所有工作于同温热源与同温冷源之间的可逆 热机,其热机效率都相等,即与热机的工作物质 无关。 10
10 2 W Q − = 1 2 1 T T = − 2 1 1 2 2 2 1 W Q Q Q Q Q Q − + = = = + 1 2 1 2 0 Q Q T T + = 1. 热机的效率 卡诺定理 I R 所有工作于同温热源和同温冷源之间的热机, 其效率都不能超过可逆机(即卡诺热机),即可逆机 的效率最大。 所有工作于同温热源与同温冷源之间的可逆 热机,其热机效率都相等,即与热机的工作物质 无关