
二 概率 (一)概率的统计定义 研究随机试验,仅知道可能发生哪些随机 事件是不够的,还需了解各种随机事件发生的 可能性大小,以揭示这些事件的内在的统计规 律性,从而指导实践。这就要求有一个能够刻 划事件发生可能性大小的数量指标,这指标应 该是事件本身所固有的,且不随人的主观意志 而改变,人们称之为概率(probability)。 事件A的概率记为P(A) 上一张下一张主页退出
二 、 概 率 (一)概率的统计定义 研究随机试验,仅知道可能发生哪些随机 事件是不够的,还需了解各种随机事件发生的 可能性大小,以揭示这些事件的内在的统计规 律性,从而指导实践。这就要求有一个能够刻 划事件发生可能性大小的数量指标,这指标应 该是事件本身所固有的,且不随人的主观意志 而改变,人们称之为概率(probability)。 事件A的概率记为P(A)。 上一张 下一张 主 页 退 出

概率的统计定义在相同条件下进行n次重 复试验, 如果随机事件A发生的次数为,那么 m/n称为随机事件A的频率(frequency); 当试验重复数n逐渐增大时,随机事件A的频率 越来越稳定地接近某一数值p,那么就把p 称为随机事件A的概率。 上一张下一张主页退出
概率的统计定义 在相同条件下进行n次重 复试验,如果随机事件A发生的次数为m,那么 m/n称为随机事件A的频率(frequency); 当试验重复数n逐渐增大时,随机事件A的频率 越来越稳定地接近某一数值 p , 那么 就 把 p 称为随机事件A的概率。 上一张 下一张 主 页 退 出

这样定义的概率称为统计概率 (statistics probability),或者称后验概 (posterior probability) 例如为了确定抛掷一枚硬币发生正面朝上 这个事件的概率,历史上有人作过成干上万次 抛掷硬币的试验。在表4一1中列出了他们的试 验记录。 上一张下一张主页退出
这 样 定 义 的 概 率 称 为 统 计 概 率 (statistics probability),或者称后验概 率(posterior probability)。 例如 为了确定抛掷一枚硬币发生正面朝上 这个事件的概率 ,历史上有人作过成千上万次 抛掷硬币的试验。在表4—1中列出了他们的试 验记录。 上一张 下一张 主 页 退 出
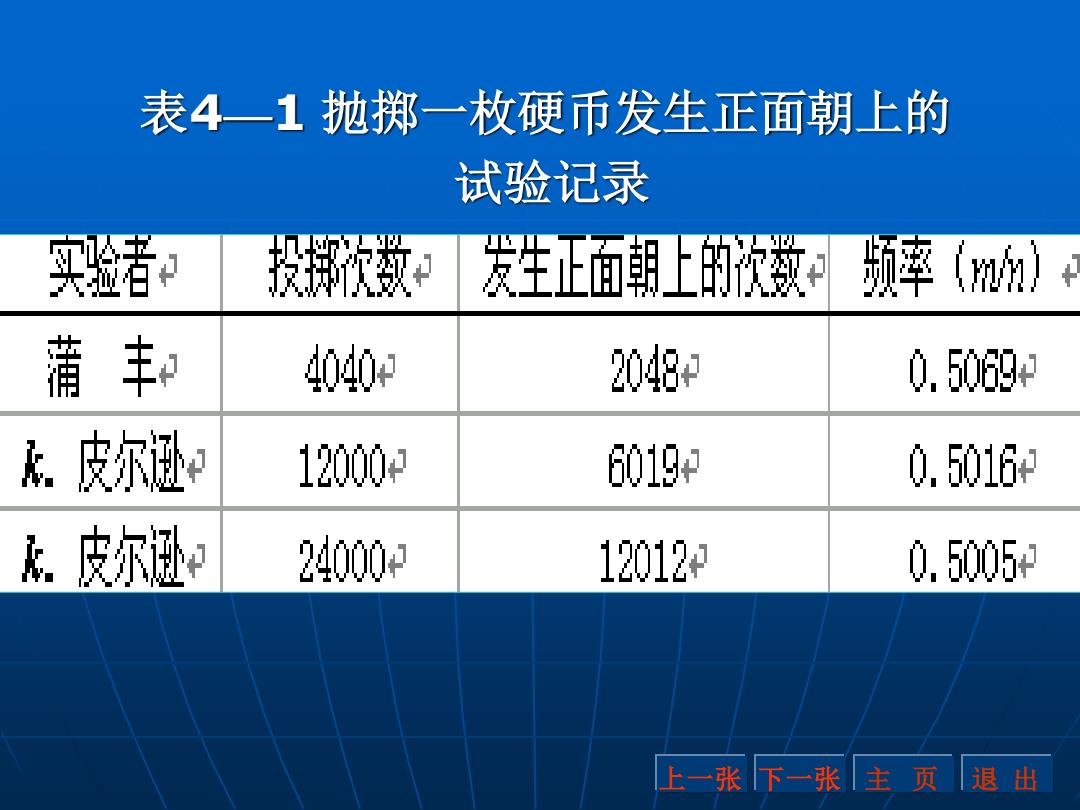
表4一1抛掷一枚硬币发生正面朝上的 试验记录 买验绪和 投救 发生正面朝上的次数: 频率(m领】 蒲丰和 4040中 2048- 0.5069 k皮尔逊 12000 6019 0.5016 k皮尔逊 24000 12012 0.5005+ 上一张下一张主页退出
表4—1 抛掷一枚硬币发生正面朝上的 试验记录 上一张 下一张 主 页 退 出

从表4-1可看出, 随着实验次数的增多 正面朝上这个事件发生的频率越来越稳定地接 近0.5,我们就把0.5作为这个事件的概率。 在一般情况下,随机事件的概率p是不可 能准确得到的。通常以试验次数充分大时随机 事件A的频率作为该随机事件概率的近似值。 即P(A)=p≈m/n(n充分大) (4-1) 上一张下一张主页退出
从表4-1可看出,随着实验次数的增多, 正面朝上这个事件发生的频率越来越稳定地接 近0.5,我们就把0.5作为这个事件的概率。 在一般情况下,随机事件的概率p是不可 能准确得到的。通常以试验次数n充分大时随机 事件A的频率作为该随机事件概率的近似值。 即 P(A)=p≈m/n (n充分大)(4-1) 上一张 下一张 主 页 退 出