
响应面(RESPONSE SURFACE)分析讲义 徐向宏编 (甘肃农业大学) 2009年2月
响应面(RESPONSE SURFACE)分析讲义 徐向宏 编 (甘肃农业大学) 2009 年 2 月
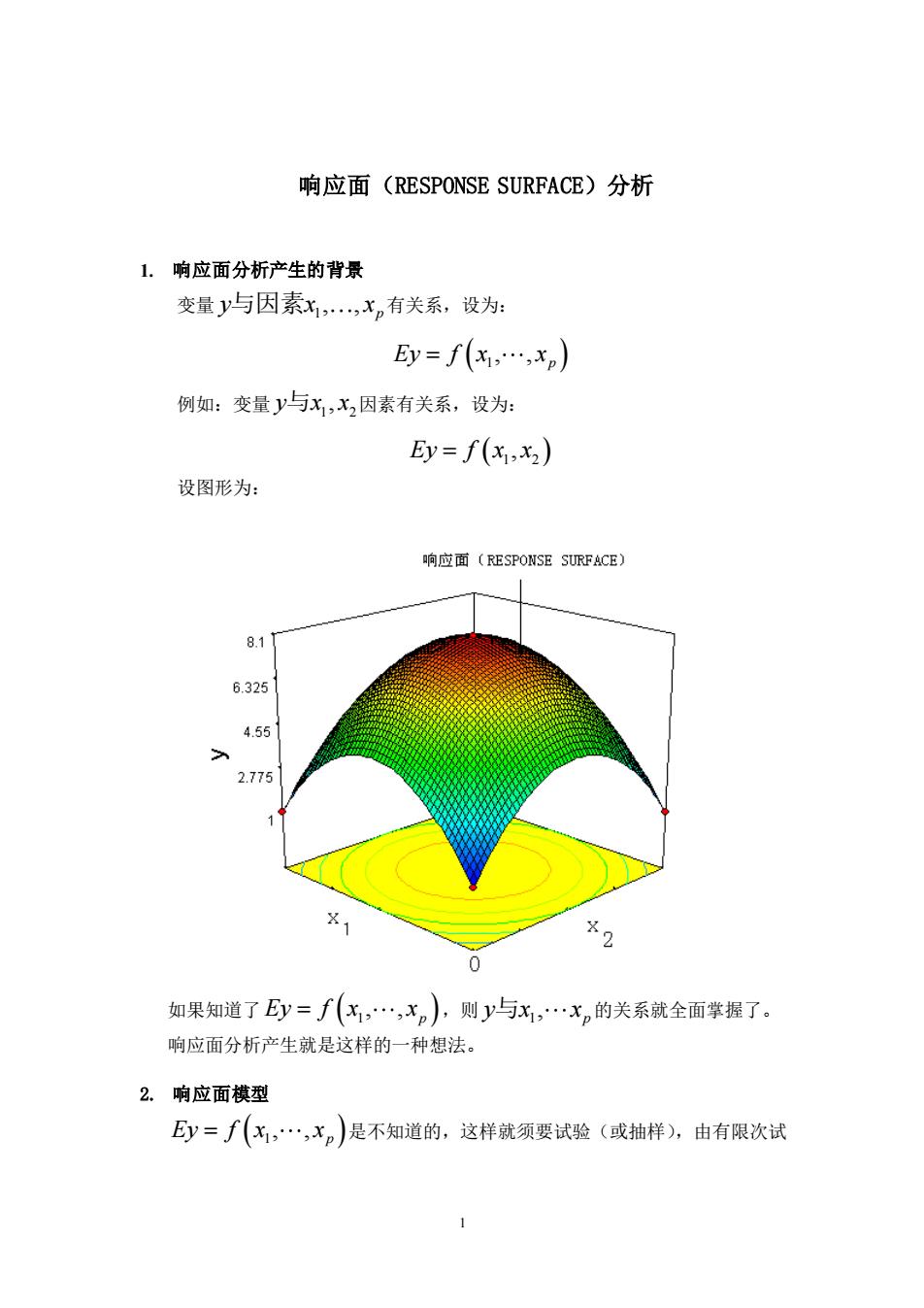
响应面(RESPONSE SURFACE)分析 1.响应面分析产生的背景 变量y与因素x,,x,有关系,设为: Ey=f(x,…,xp) 例如:变量y与x,x2因素有关系,设为: Ey=f(xx2) 设图形为: 响应面(RESPONSE SURFACE) 8.1 6.325 4.55 2.775 1 X 2 0 如果知道了y=f(x,,xp),则y与x,…x,的关系就全面掌握了。 响应面分析产生就是这样的一种想法。 2.响应面模型 y=∫(飞,…,xp)是不知道的,这样就须要试验(或抽样),由有限次试
1 响应面(RESPONSE SURFACE)分析 1. 响应面分析产生的背景 变量 1 , , p y x x 与因素 有关系,设为: Ey f x x = ( 1 , , p ) 例如:变量 1 2 y x x 与 , 因素有关系,设为: Ey f x x = ( 1 2 , ) 设图形为: 如果知道了 Ey f x x = ( 1 , , p ) ,则 1 , p y x x 与 的关系就全面掌握了。 响应面分析产生就是这样的一种想法。 2. 响应面模型 Ey f x x = ( 1 , , p ) 是不知道的,这样就须要试验(或抽样),由有限次试

验所得试验数据来估计y=f(x,…,x)(由部分来说明全体)。 哪么用什么样的模型来估计Ey=∫(x,…,x。)呢?在数学分析上已有麦 克劳林或泰勒展开式即:f(,)÷f(0)+(O) .f"(0) x2. 1 21 般都能满足(收敛),又生物科学领域变量间的特点,因此用 y=f(x,…,xp)≈a+bx+…+cxp+…+d2+…+ex,2+ X2…+g,-X,模型。 综上所述:试验得试验点: (x1,…xp1y),,(xa,xnmy) 估计出 y=f(x,…,xp)≈a+bx+…+cxp+…+d2+…+ex,2+ x2…+g,-1Xn的系数a,b,…,如果可用(检验),则X,…x,与y的关 系就全面掌握了。 3.响应面分析的试验设计(DOE一一Design of Exprement)一用Design-Expert7 软件 试验点(x1,…xp1乃?),…,(xn,…Xmn2 yn?)选择哪些点才能比较科 学地反映客观实际呢(包括试验次数要尽可能少、自变量间正交等)?这就是称 为试验设计研究。响应面分析的试验设计有: 中心组合设计(Central Composite Design-一CCD,二次正交旋转组合设计); BOX设计(Box-Behnken设计): D-optimal设计(2次饱和D一最优设计) 均匀设计: 田口设计: * 常用的是中心复合设计、BOX设计。现仅就这2个设计进行举例说明。 设:y=f(x,x2,x)≈a+bx+…+cx,+d2+…+ex2+ +fx2+…+gx2X3
2 验所得试验数据来估计 Ey f x x = ( 1 , , p ) (由部分来说明全体)。 哪么用什么样的模型来估计 Ey f x x = ( 1 , , p ) 呢?在数学分析上已有麦 克劳林或泰勒展开式即: ( ) ( ) ( ) ( ) ' 2 0 " 0 0 1! 2! f f f x f x x + + + 一般都能满足(收敛),又生物科学领域变量间的特点,因此用 ( ) 2 2 1 1 1 , , Ey f x x a bx cx dx ex = + + + + + + + + p p p 1 2 1 p p fx x gx x + − 模型。 综上所述:试验得试验点: ( x x y x x y 11 1 1 1 , , , , , , p n pn n ) ( ) 估计出 ( ) 2 2 1 1 1 , , Ey f x x a bx cx dx ex = + + + + + + + + p p p 1 2 1 p p fx x gx x + − 的系数 a b, , ,如果可用(检验),则 1 , p x x y 与 的关 系就全面掌握了。 3. 响应面分析的试验设计(DOE——Design of Exprement)—用 Design-Expert7 软件 试验点 ( x x y x x y 11 1 1 1 , , ? , , , , ? p n pn n ) ( ) 选择哪些点才能比较科 学地反映客观实际呢(包括试验次数要尽可能少、自变量间正交等)?这就是称 为试验设计研究。响应面分析的试验设计有: 中心组合设计(Central Composite Design—CCD,二次正交旋转组合设计); BOX 设计(Box-Behnken 设计); D-optimal设计(2次饱和D—最优设计) 均匀设计; 田口设计; …。 常用的是中心复合设计、BOX 设计。现仅就这 2 个设计进行举例说明。 设: ( ) 2 2 1 2 3 1 3 1 3 Ey f x x x a bx cx dx ex = + + + + + + + , , 1 2 2 3 + + + fx x gx x
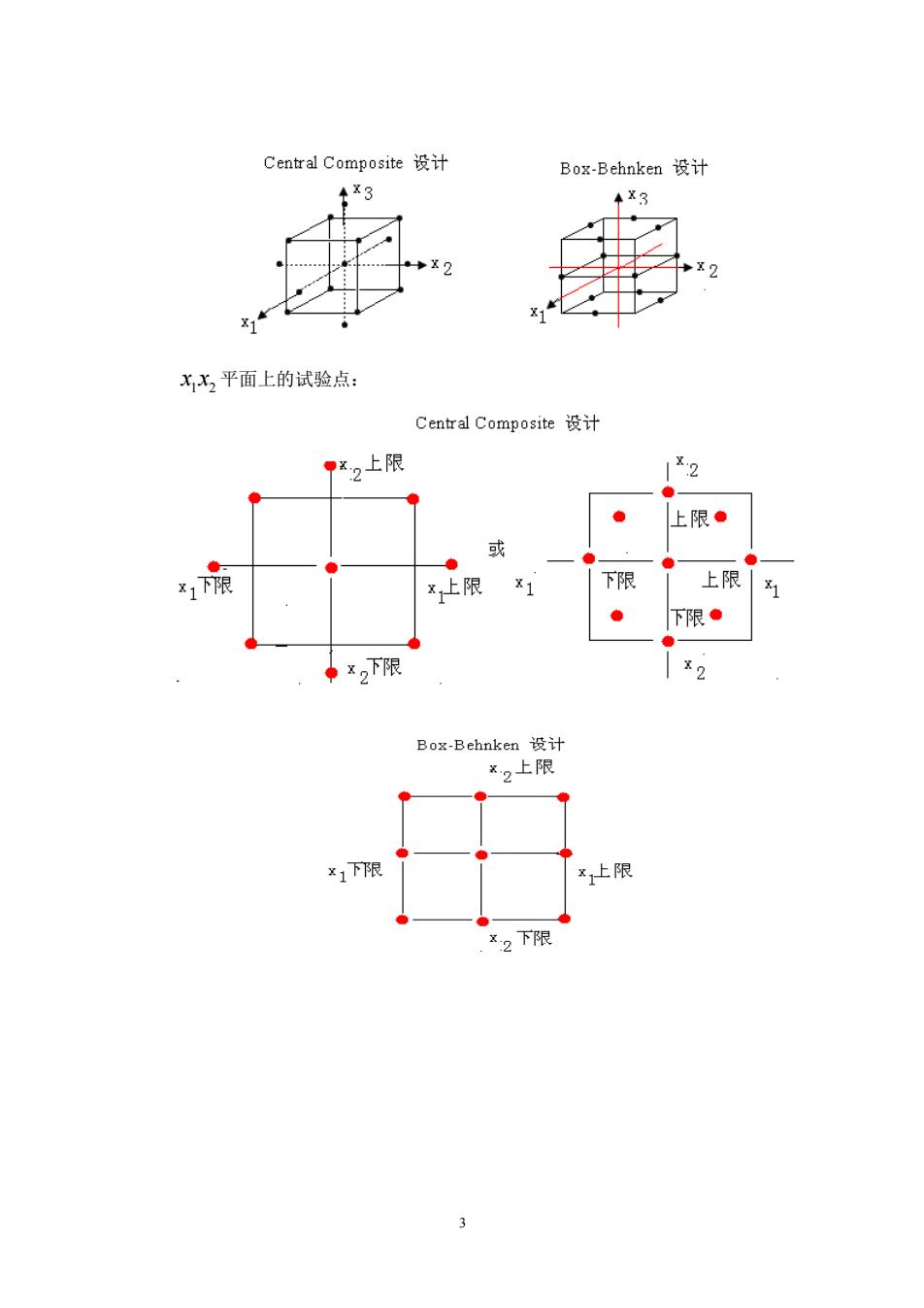
Central Composite设计 Box-Behnken设计 4x3 +x3 ¥2 Xx2平面上的试验点: Central Composite设计 72上限 ● 上限● 或 ● X1下限 限 4y 下限 上限 1 下限● x2下限 Box-Behnken设计 ×2上限 x1下限 ×上限 x:2下限 3
3 1 2 xx 平面上的试验点:
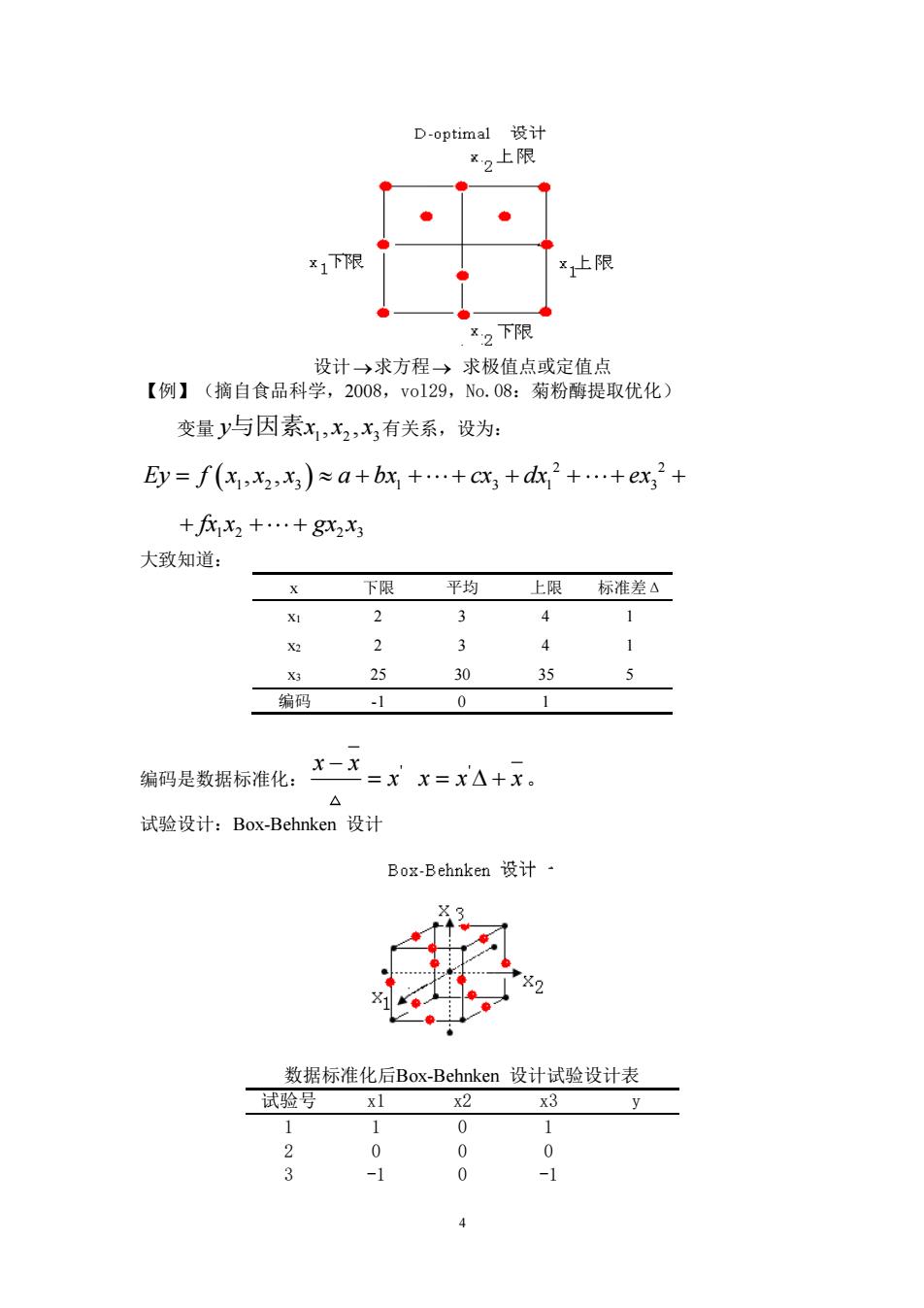
D-optimal设计 ×2上限 1下限 上限 *2下限 设计→求方程)求极值点或定值点 【例】(摘自食品科学,2008,vo129,No.08:菊粉酶提取优化) 变量y与因素x,x2,x3有关系,设为: y=f(x,2,x3)≈a+bx+…+cx3+d2+…+x2+ +x2+…+8x2X3 大致知道: 下限 平均 上限 标准差△ X1 2 3 4 1 X2 2 J 1 X3 25 30 35 5 编码 -1 0 1 x-x 编码是数据标准化: =xx=x△+x。 △ 试验设计:Box-Behnken设计 Box-Behnken设计· 1 数据标准化后Box-Behnken设计试验设计表 试验号 xl x2 X3 1 1 0 1 2 0 0 0 -1 0 -1
4 设计 → 求方程 → 求极值点或定值点 【例】(摘自食品科学,2008,vol29,No.08:菊粉酶提取优化) 变量 1 2 3 y x x x 与因素 , , 有关系,设为: ( ) 2 2 1 2 3 1 3 1 3 Ey f x x x a bx cx dx ex = + + + + + + + , , 1 2 2 3 + + + fx x gx x 大致知道: x 下限 平均 上限 标准差Δ x1 2 3 4 1 x2 2 3 4 1 x3 25 30 35 5 编码 -1 0 1 编码是数据标准化: x x ' ' x x x x − = = + 。 试验设计:Box-Behnken 设计 数据标准化后Box-Behnken 设计试验设计表 试验号 x1 x2 x3 y 1 1 0 1 2 0 0 0 3 -1 0 -1