
Lecture 5 Conduction equation and examples 孙建奇
Lecture 5 Conduction equation and examples 孙建奇
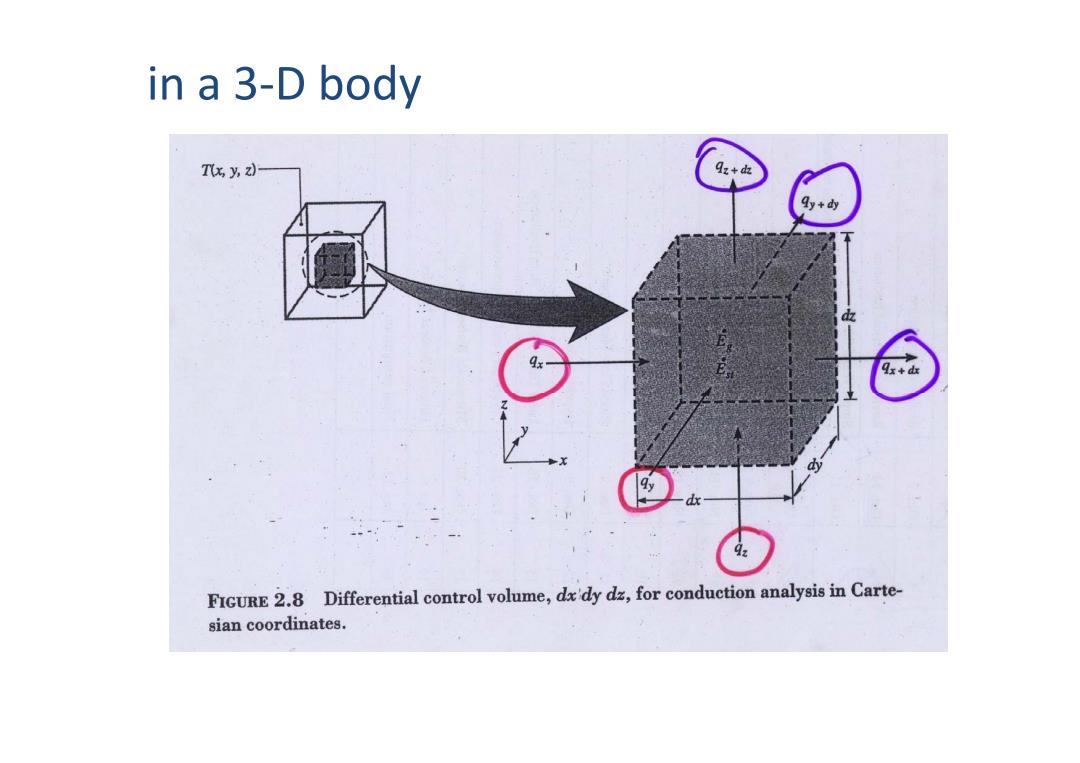
in a 3-D body Tx y,2)- Qz+de y+dy dx 4: FIGURE 2.8 Differential control volume,dx'dy dz,for conduction analysis in Carte- sian coordinates
in a 3-D body

。Energy Balance Ein+Ea Eou =Est Tdxdydz q4.+,+q.+9ddb-9r+h-9,+-9:+t=per oa;dx dy dx ∂a dy-d正 T dxdyd qdxdyd=pc,di aT 9s =-kdydz dx 9,=-hdrde O dy OT g:=-kaxdy dz ∂T ∂ (k 一)+ (k ay )+ dy z 3T)+4
.. . . Ein q out st +− = EE E • Energy Balance . x y z x dx y dy z dz p T q q q q dxdydz q q q c dxdydz dt +++ ρ ∂ +++ − − − = x T q kdydz dx ∂ = − y T q kdxdz dy ∂ = − z T q kdxdy dz ∂ = − . x y z p q q q T dx dy dz q dxdydz c dxdydz dx dy dz dt ρ ∂ ∂ ∂ ∂ −−−+ = ( ) ( ) ( ) ''' p TT T T C k k kq txx yy zz ρ ∂ ∂∂ ∂∂ ∂∂ =+++ ∂∂ ∂ ∂ ∂ ∂ ∂
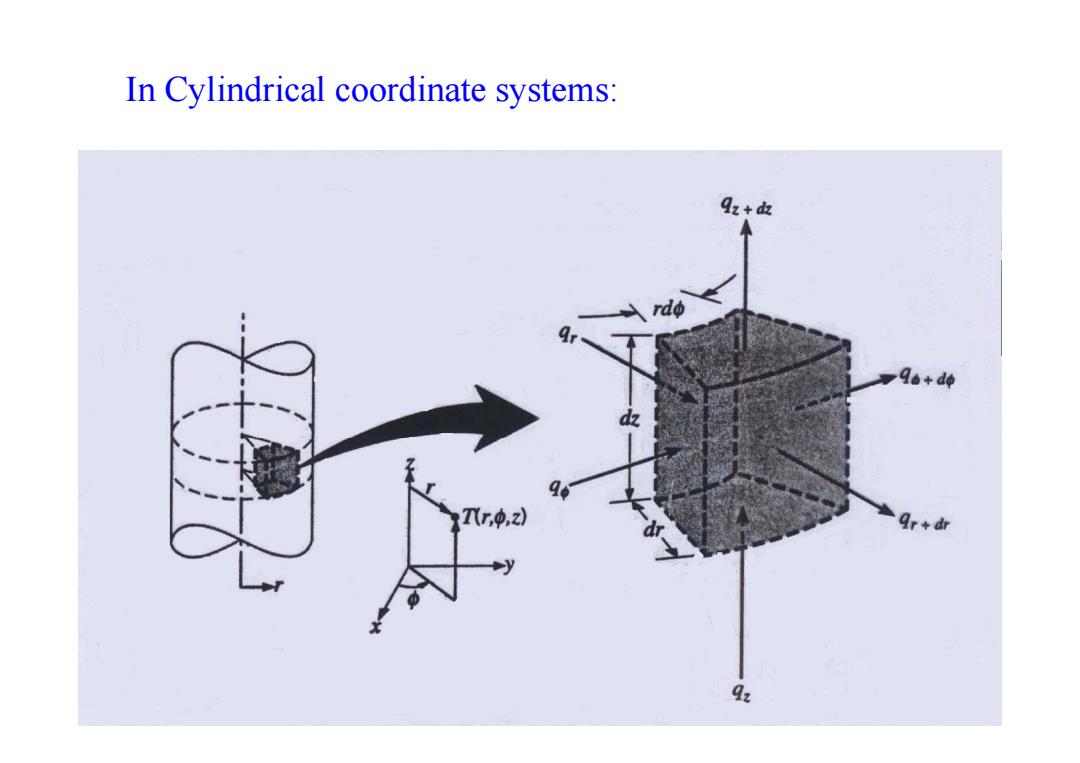
In Cylindrical coordinate systems: qz+血 Qa+do d Tr,z) 9r+d由 Qx
In Cylindrical coordinate systems:

In Cylindrical coordinate systems: OT 1a aT、,ka2T,,a2T pcp-(ra+0+k2+g” Boundary conditions: T(ro)=T1 -k81。=9g-k80=0 aT -k8n=hs-T)
In Cylindrical coordinate systems: Boundary conditions: