
二质点的衰减振动 (三)衰减振动的能量 由于阻尼的存在,质点振动系统的能量将 随时间作指数规律衰减; E- 动5e
(三)衰减振动的能量 由于阻尼的存在,质点振动系统的能量将 随时间作指数规律衰减; 二 质点的衰减振动 2 2 0 0 1 1 2 T t E Edt S e m T δ ξ − = ≈ ∫
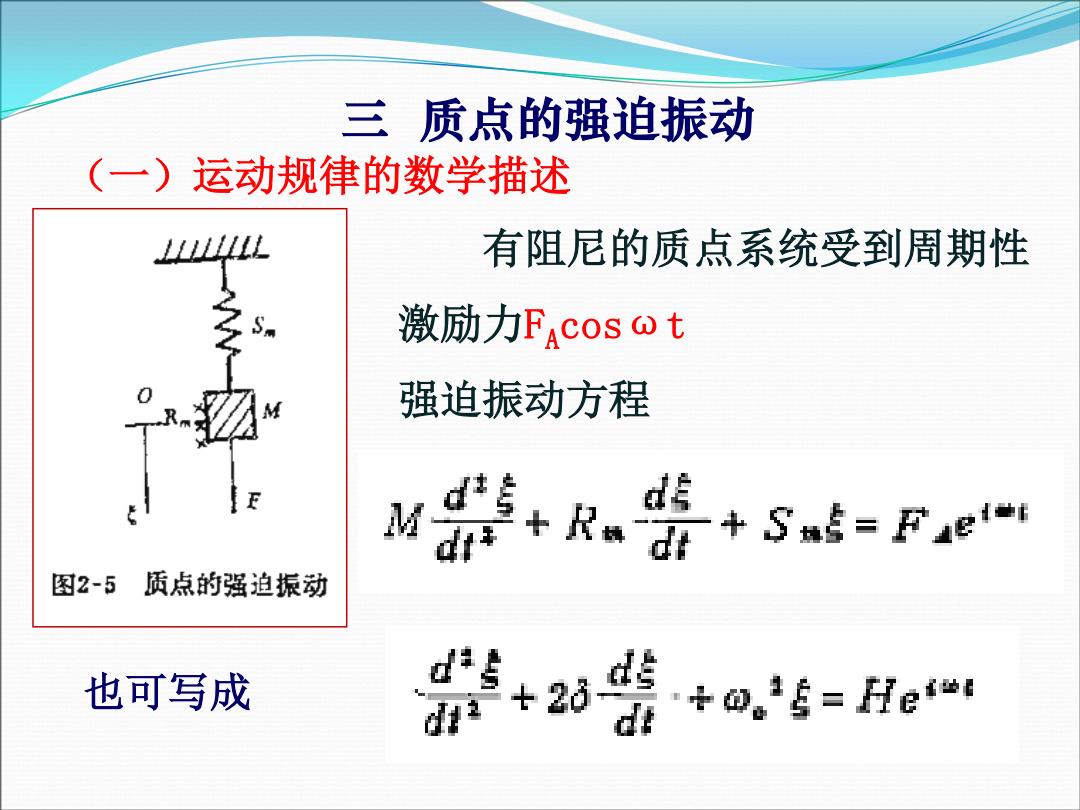
三质点的强迫振动 (一)运动规律的数学描述 有阻尼的质点系统受到周期性 激励力FAcos@t 强迫振动方程 +R+S=Fe 图2-5质点的强迫振动 也可写成 +2i盟+a,f=He
三 质点的强迫振动 有阻尼的质点系统受到周期性 激励力FAcosωt 强迫振动方程 也可写成 (一)运动规律的数学描述

三质点的强迫振动 5=,e8c0sw'1-,)+套cos(ot-8。-) 强迫振动由两部分合成。第一部分随时间 延长,逐渐衰减,阻尼系数越大,衰减越快, 是暂态运动;第二部分是等幅振动,其频率等 于激振力频率,其振幅和相位与系统的常数有 关,这就是稳态运动。 稳态振动基本建立的时间τo, 称为过渡过程时间
强迫振动由两部分合成。第一部分随时间 延长,逐渐衰减,阻尼系数越大,衰减越快, 是暂态运动;第二部分是等幅振动,其频率等 于激振力频率,其振幅和相位与系统的常数有 关,这就是稳态运动。 稳态振动基本建立的时间τ0,称为过渡过程时间。 三 质点的强迫振动
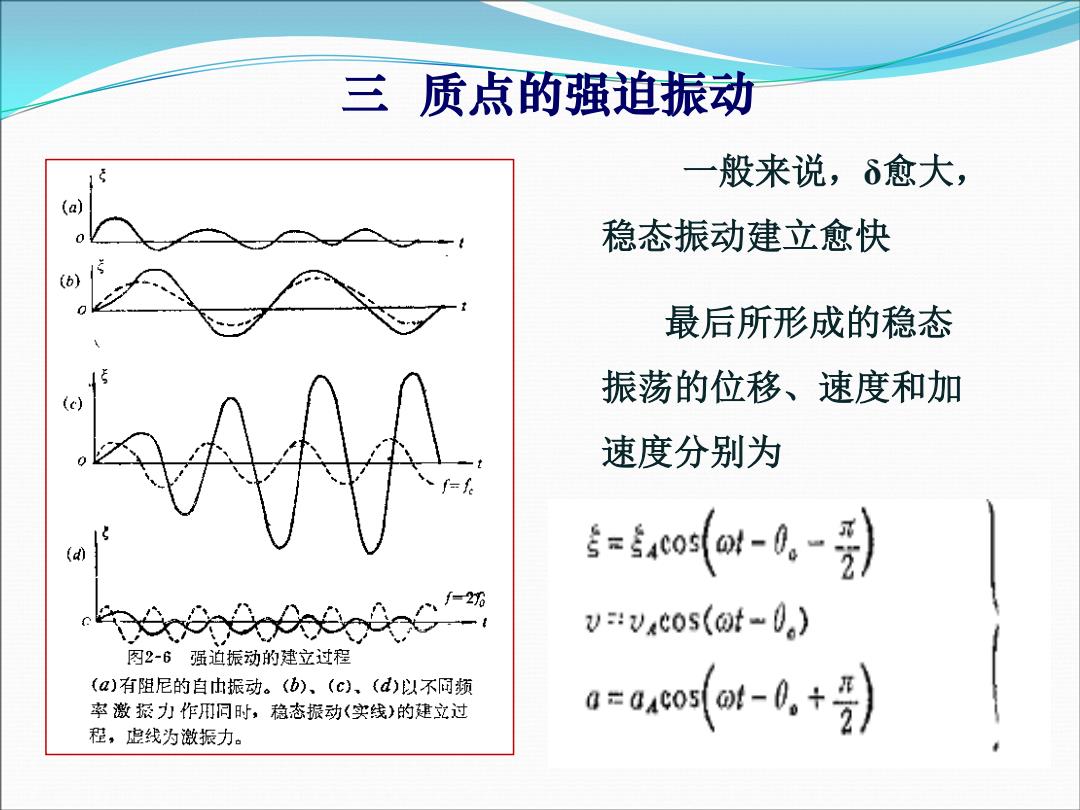
三质点的强迫振动 19 一 般来说,δ愈大, (a) 稳态振动建立愈快 (6) 最后所形成的稳态 振荡的位移、速度和加 速度分别为 (d0 s=co(ad-4.-》 4o60o6o6olocm v=:vcos(t-0) 图2-6强迫振动的建立过程 (a)有阻尼的自h振动。(b)、(c)、(d)以不同频 率激振力作用同时,稳态振动(实线)的建立过 a=0ueos(ot-0,+f》 程,虚线为激振力
一般来说,δ愈大, 稳态振动建立愈快 最后所形成的稳态 振荡的位移、速度和加 速度分别为 三 质点的强迫振动

三质点的强迫振动 =Zale"e (2-35) 2-R2+(@M-8》 0=81为=g10M- R (2-36) Zm称为力阻抗,其单位用力欧姆表示, 1力欧姆=1牛顿*秒/米.Rm为力阻,Xm为力抗, 0,为相位角
Zm称为力阻抗,其单位用力欧姆表示, 1力欧姆=1牛顿*秒/米.Rm为力阻,Xm为力抗, θ0为相位角 三 质点的强迫振动