
质点的自由振动 频率f 周期性振动在单位时间内的周 期数; 频率单位用赫兹表示Hz 当质点做自由振动时,其频率 2 仅同固有参量S和M有关,而与初 M 始条件无关,故也称固有频率 质量越大,力劲越小,固有频率就越低
M S f m 2π 1 0 = T f 1 = 频率单位用赫兹表示 Hz 当质点做自由振动时,其频率 仅同固有参量Sm和M有关,而与初 始条件无关,故也称固有频率。 质量越大,力劲越小,固有频率就越低。 一 质点的自由振动 频率f 周期性振动在单位时间内的周 期数;

一质点的自由振动 (二)自由振动的能量关系 初始时刻振子从外部获得位能或动能, 此后系统振动能量是两种能量之和; 两种能量分配比例有变化,最大位移时 是最大势能,最大速度时势能为0,动能最 大; 自由振动系统是一个能量守恒系统
(二)自由振动的能量关系 初始时刻振子从外部获得位能或动能, 此后系统振动能量是两种能量之和; 两种能量分配比例有变化,最大位移时 是最大势能,最大速度时势能为0,动能最 大; 自由振动系统是一个能量守恒系统 一 质点的自由振动

二质点的衰减振动 (一)运动规律的数学描述 阻力导致了衰减,速度不大时,可以认为阻力与速度 成线性关系,其方向与质点运动方向相反; Fg=-Rm de dt R称为阻力系统,是正常数 M d 5+S.5=0 d dt2 +285+5=0 dt δ= 称为阻尼系数 2M
阻力导致了衰减,速度不大时,可以认为阻力与速度 成线性关系,其方向与质点运动方向相反; R m d F R dt ξ = − 2 2 0 m m d d MRS dt dt ξ ξ + += ξ 0 dt d 2 dt d 2 2 0 2 + +ω ξ = ξ δ ξ 2 R m M δ = 称为阻尼系数 (一)运动规律的数学描述 Rm称为阻力系统,是正常数 二 质点的衰减振动
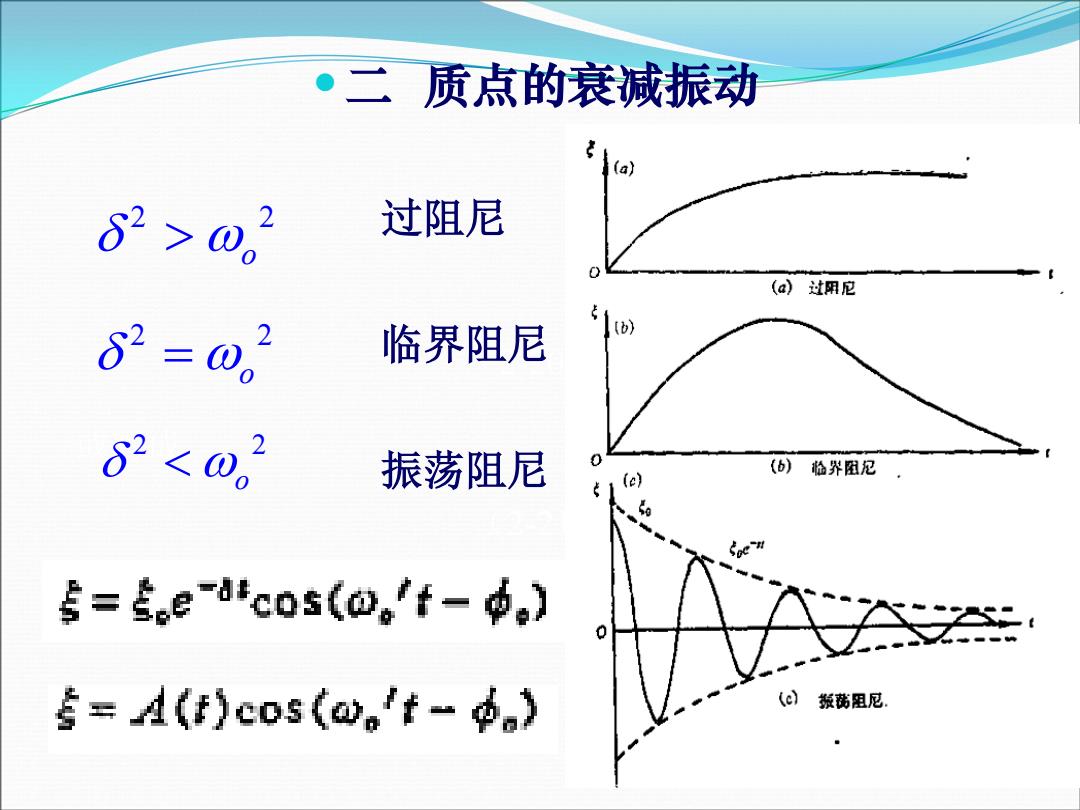
·二质点的衰减振动 62 2 > 过阻尼 (a)过用尼 2 2 临界阻尼 δ2<。 振荡阻尼 (6)临界阻尼 (e) 5=eco5(of-】 0 专=At)c0s(.'t~a) (叛阻尼
或写成 (2-20) (2-21) 2 2 o δ ω> 2 2 o δ ω= 2 2 o δ ω< 过阻尼 临界阻尼 振荡阻尼 二 质点的衰减振动
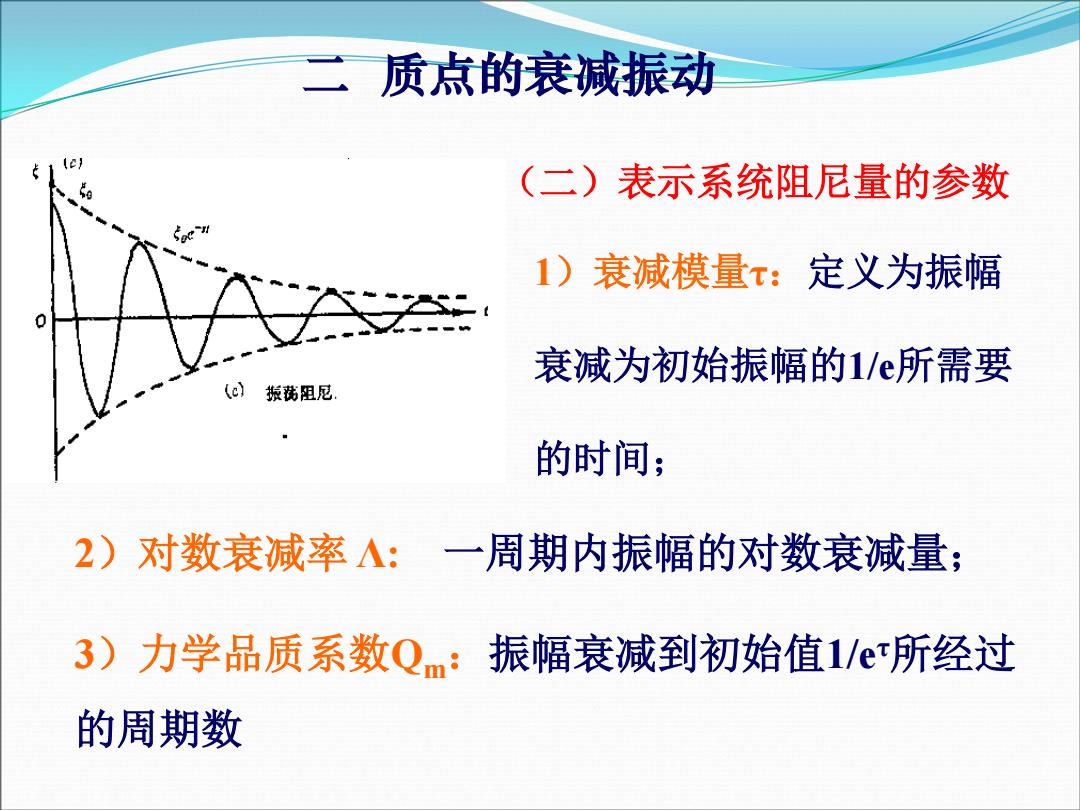
二质点的衰减振动 (二)表示系统阻尼量的参数 1)衰减模量τ:定义为振幅 衰减为初始振幅的1/e所需要 (c) 振黄阻尼 的时间; 2)对数衰减率人:一周期内振幅的对数衰减量; 3)力学品质系数Qm:振幅衰减到初始值1/e所经过 的周期数
(二)表示系统阻尼量的参数 1)衰减模量τ:定义为振幅 衰减为初始振幅的1/e所需要 的时间; 二 质点的衰减振动 2)对数衰减率 Λ: 一周期内振幅的对数衰减量; 3)力学品质系数Qm:振幅衰减到初始值1/eτ所经过 的周期数