弯曲变形由数学知识可知:yld'yM(x) >0M(x) > 0dr??=+pdy1>0/1+dxx0略去高阶小量,得y4d'y1M(x)< 0M(x)<0dr?pd'y<0dx2X1d'yM(x)所以0dr?EL
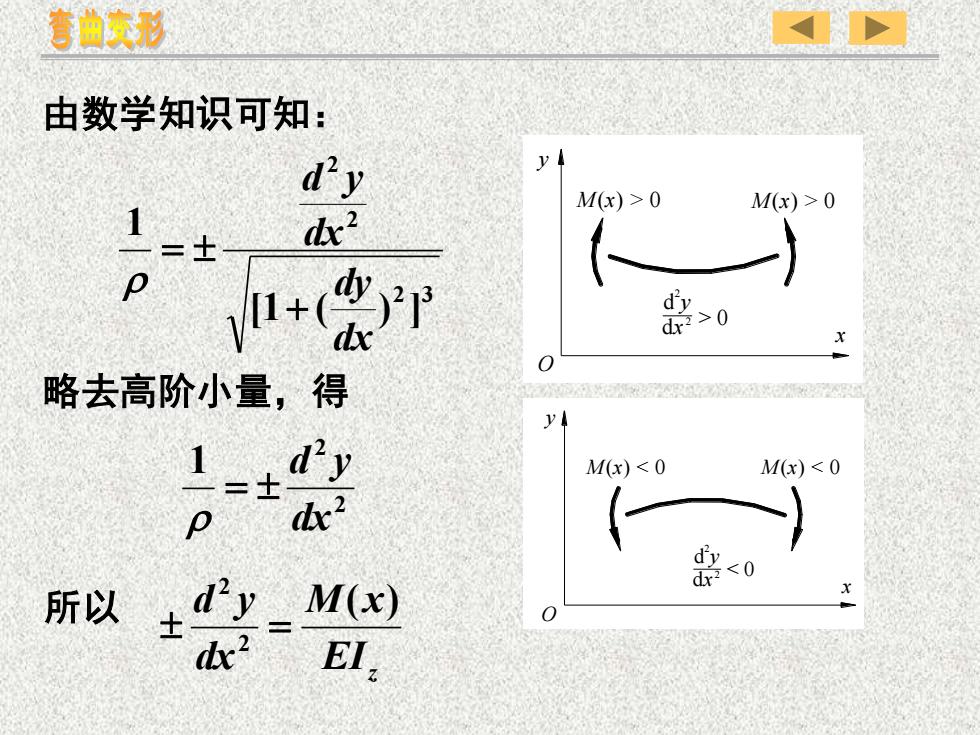
由数学知识可知: 2 3 2 2 [1 ( ) ] 1 dx dy dx d y + = 略去高阶小量,得 2 2 1 dx d y = 所以 EIz M x dx d y ( ) 2 2 = 2 M(x) > 0 M(x) > 0 O d y dx 2 > 0 x y M(x) < 0 O dx d y 2 < 0 2 y x M(x) < 0

弯曲变形由弯矩的正负号规定可得,弯矩的符号与曲线的二阶导数符号一致,所以曲线的近似微分方程为:M(x)QMdr2EI由上式进行积分,就可以求出梁横截面的转角和挠度
由弯矩的正负号规定可得,弯矩的符号与挠曲 线的二阶导数符号一致,所以挠曲线的近似微分方 程为: EI z M x dx d w ( ) 2 2 = 由上式进行积分,就可以求出梁横截面的转角 和挠度

弯曲变形dwM(x)EIM(x)dxEL.dx积分一次得转角方程为:dwW= EI,0=[ M(x)dx +CEIdx再积分一次得挠度方程为:El, w= JJ M(x)dxd+ Cx+ D
EI z M x dx d w ( ) 2 2 = 积分一次得转角方程为: = EI = M x dx +C dx dw EIz z ( ) ( ) 2 2 M x dx d w EIz = 再积分一次得挠度方程为: EIz w = M (x)dxdx+Cx + D

弯曲变形积分常数C、D由梁的位移边界条件和光滑连续条件确定。光滑连续条件位移边界条件AAAHAAA易w.=0WAL=WARW.=△WAL = WARw. =00 =0△一弹簧变形0 AL = 0AR
积分常数C、D 由梁的位移边界条件和光滑连续 条件确定。 A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ A A A A A A ~ ~ ~ ~ ~ wA = 0 wA = 0 A = 0 wA = 位移边界条件 光滑连续条件 wAL = wAR AL = AR wAL = wAR -弹簧变形

弯曲变形讨论:①适用于小变形情况下,、线弹性材料,细长构件的平面弯曲②可应用于求解承受各种载荷的等截面或变截面梁的位移。③积分常数由挠曲线变形的几何相容条件(边界条件、连续条件)确定。①优点:使用范围广,直接求出较精确;缺点:计算较繁
讨论: ①适用于小变形情况下、线弹性材料、细长构件的平面弯曲。 ②可应用于求解承受各种载荷的等截面或变截面梁的位移。 ③积分常数由挠曲线变形的几何相容条件(边界条件、连续 条件)确定。 ④优点:使用范围广,直接求出较精确; 缺点:计算较繁