
2.Snake模型的数学模型 Em是内部能量,控制蛇模型特性,定义为 Emr=1/2(xv'(sI2+31v"(s)|2) v'(s)v"(s)是V对s的一阶和二阶导数,系数a 分别是控制蛇模型的弹性和刚性,这些参数操纵着模型的物 理行为和局部连续性 外部能量E决定着向某种固定的特征移动蛇模型,吸引蛇 模型到显著的图像特征。因为这些特征只能根据特定的问 题而定义,所以一般的外部能量函数不易确定。因此,Et 没有统一的数学表达式,必须从问题本身的特性出发,根据 实际情况处理
2.Snake模型的数学模型 外部能量Eext 决定着向某种固定的特征移动蛇模型,吸引蛇 模型到显著的图像特征。因为这些特征只能根据特定的问 题而定义,所以一般的外部能量函数不易确定。因此, Eext 没有统一的数学表达式,必须从问题本身的特性出发,根据 实际情况处理 Eint是内部能量,控制蛇模型特性,定义为 分别是v 对s 的一阶和二阶导数,系数α、β 分别是控制蛇模型的弹性和刚性, 这些参数操纵着模型的物 理行为和局部连续性

外部能量(Eex) 图像能量 定义函数EeK,以, 反映的是对图像特征(如边 界)的兴趣程度 Eon=∫Eimage(v(s)ds S Emage(xy)涵数的定义是一个关键问题. 典型的例子为 E age (x,y)=-VI(x,y E image (x,y)=-V(G(x,y)*1(x,y)) 蘭
外部能量 (Eext ) ▪ 图像能量 ▪ 定义函数 Eimage(x,y) ,反映的是对图像特征(如边 界)的兴趣程度 Eimage (x,y)函数的定义是一个关键问题. 典型的例子为 ( ( )) ext image s E E v s ds = 2 ( , ) | , )| E x y x y image = − ( 2 ( , ) | ( ( , )* ( , )) | E x y G x y I x y image = −

能量与内外力平衡方程 专养 目标轮廓的确定就被转化成了极小化如下的能量泛函 的问题 E,a=∫(a(s)ly,P+(sly.P)+Em(s》d 由变分法的原理出发,可以将其转化为Euer方程 aVss-BVss-VE age =0 这一方程可以被看作是轮廓内外力的平衡公式, 每个力都有对应的意义,在这些力的作用下轮廓发生 形变
能量与内外力平衡方程 ▪ 目标轮廓的确定就被转化成了极小化如下的能量泛函 的问题 ▪ 由变分法的原理出发,可以将其转化为Euler 方程 ▪ 这一方程可以被看作是轮廓内外力的平衡公式. ▪ 每个力都有对应的意义,在这些力的作用下轮廓发生 形变。 1 2 2 ( ) | | ( ) | | ) ( ( )) 2 snake s ss image s E s v s v E v s ds = ( + + 0 ss ssss image − − = v v E
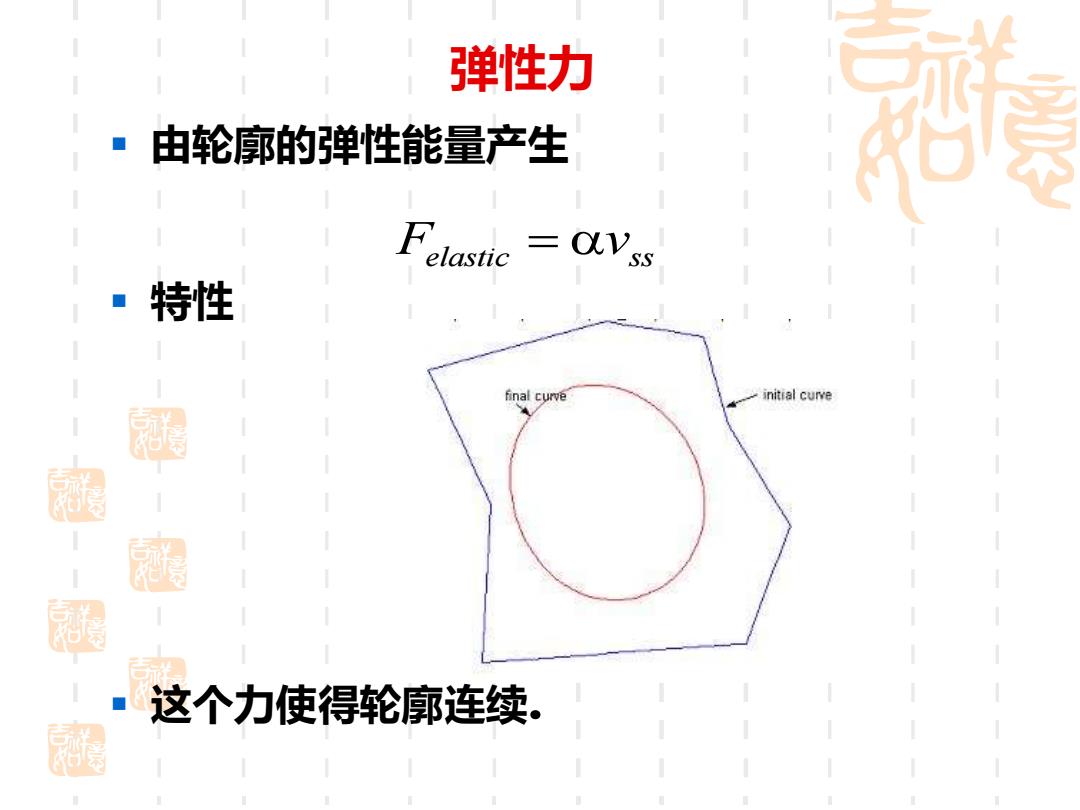
弹性力 由轮廓的弹性能量产生 Felastic =Vss elastic 特性 final curve initial curve 涵 -极 这个力使得轮廓连续。 蘭
弹性力 ▪ 由轮廓的弹性能量产生 ▪ 特性 ▪ 这个力使得轮廓连续. F v elastic ss =
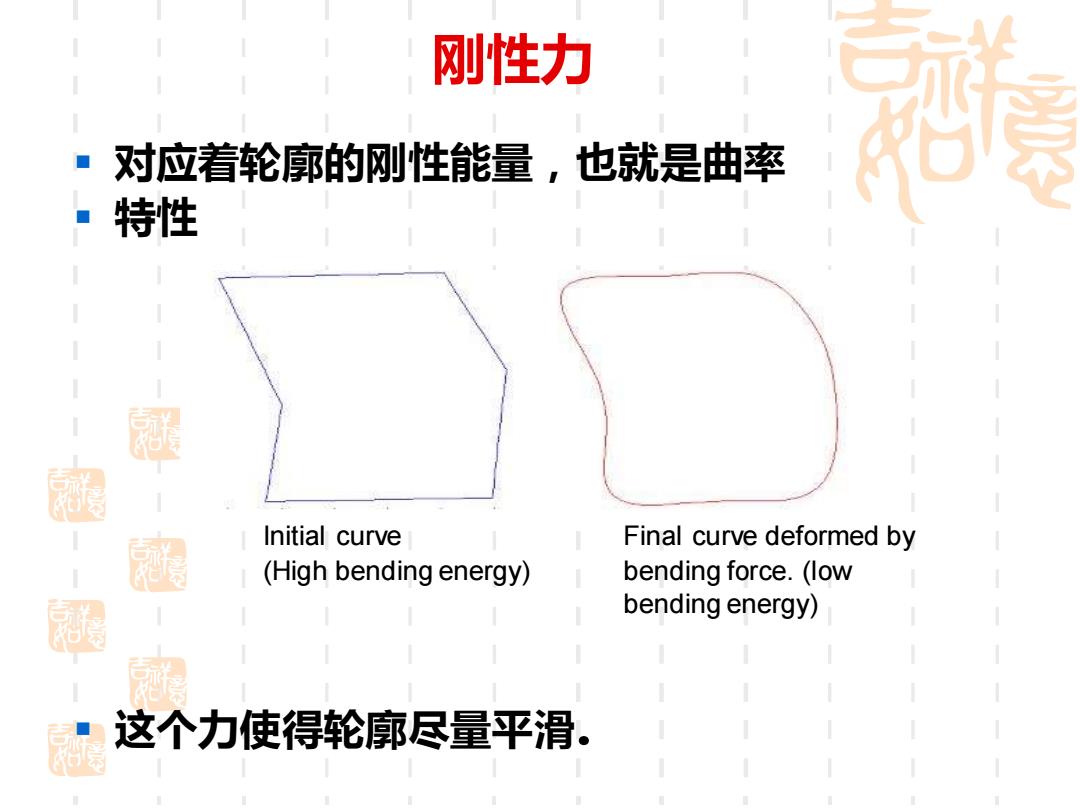
刚性力 ■ 对应着轮廓的刚性能量,也就是曲率 ■特性 涵 Initial curve Final curve deformed by (High bending energy) bending force.(low bending energy) 这个力使得轮廓尽量平滑
刚性力 ▪ 对应着轮廓的刚性能量,也就是曲率 ▪ 特性 ▪ 这个力使得轮廓尽量平滑. Initial curve (High bending energy) Final curve deformed by bending force. (low bending energy)