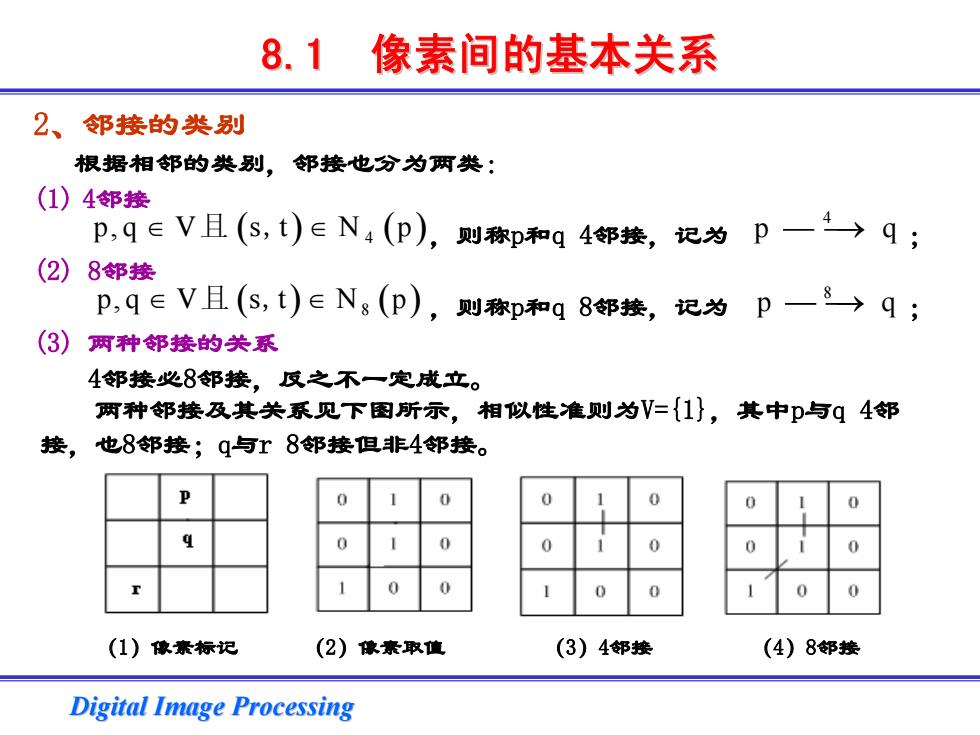
8.1 像素间的基本关系 2、邻接的类别 根据相邻的类别,邻接也分为两类: (1)4邻接 p,qeV且(S,t)∈N4(p),则称p和q4邻接,记为p一4→q; (2)8邻接 p,q∈V且(s,t)∈Ng(p),则称p和q8邻接,记为p一8→q; (3)两种邻接的关系 4邻接必8邻接,反之不一定成立。 两种邻接及其关系见下图所示,相似性准则为V={1},其中p与q4邻 接, 也8邻接;q与r8邻接但非4邻接。 0 (1)像素标记 (2)像素取值 (3)4邻接 (4)8邻接 Digital Image Processing
Digital Image Processing Digital Image Processing 2、邻接的类别 根据相邻的类别,邻接也分为两类: (1) 4邻接 ,则称p和q 4邻接,记为 ; (2) 8邻接 ,则称p和q 8邻接,记为 ; (3) 两种邻接的关系 4邻接必8邻接,反之不一定成立。 p,q V s t N p ∈ ∈ 且 , ( ) 4 ( ) 4 p ⎯ ⎯→ q p,q V s t N p ∈ ∈ 且 , ( ) 8 ( ) 8 p ⎯ ⎯→ q 8.1 像素间的基本关系 像素间的基本关系 两种邻接及其关系见下图所示,相似性准则为V={1},其中p与q 4邻 接,也8邻接;q与r 8邻接但非4邻接。 (1)像素标记 (2)像素取值 (3)4邻接 (4)8邻接

8.1 像素间的基本关系 3、通路 设p(m,n)与q(s,t)之间的各像素点形成的连线L为: L(p,q)={(m,n)=(,no),(m,n1)2,(m-1n-),(m,n,)2,(mw,nw)=(s,t)} 若(m-,n-i)与(m,n,)邻接(1≤i≤N)2则L(p,9)称 为p与q之间的一条通路,N为通路长度。与连接一样,通路也 分为4通路和8通路。 4、连通性 若S是图像中的一个子集,p,q∈S,且存在一条由S中像素 组成的从p到q的通路,则称p在图像集S中与q连通,连通也分 为4连通和8连通。 Digital Image Processing
Digital Image Processing Digital Image Processing 3、通路 设 与 之间的各像素点形成的连线L为: 若 与 邻接 ,则 称 为p与q之间的一条通路,N为通路长度。与连接一样,通路也 分为4通路和8通路。 4、连通性 若S是图像中的一个子集,p,q∈S ,且存在一条由S中像素 组成的从p到q的通路,则称p在图像集S中与q连通,连通也分 为4连通和8连通。 0 0 11 1 1 L pq mn m n m n m n m n m n st (,) ={( , ) ( , ),( , ),...,( , ),( , ),...,( , ) ( , ) = = i i ii NN − − } p( ,) m n qst (,) 1 1 (,) m n i i − − (,) m ni i (1 ) ≤ i N ≤ L(,) p q 8.1 像素间的基本关系 像素间的基本关系
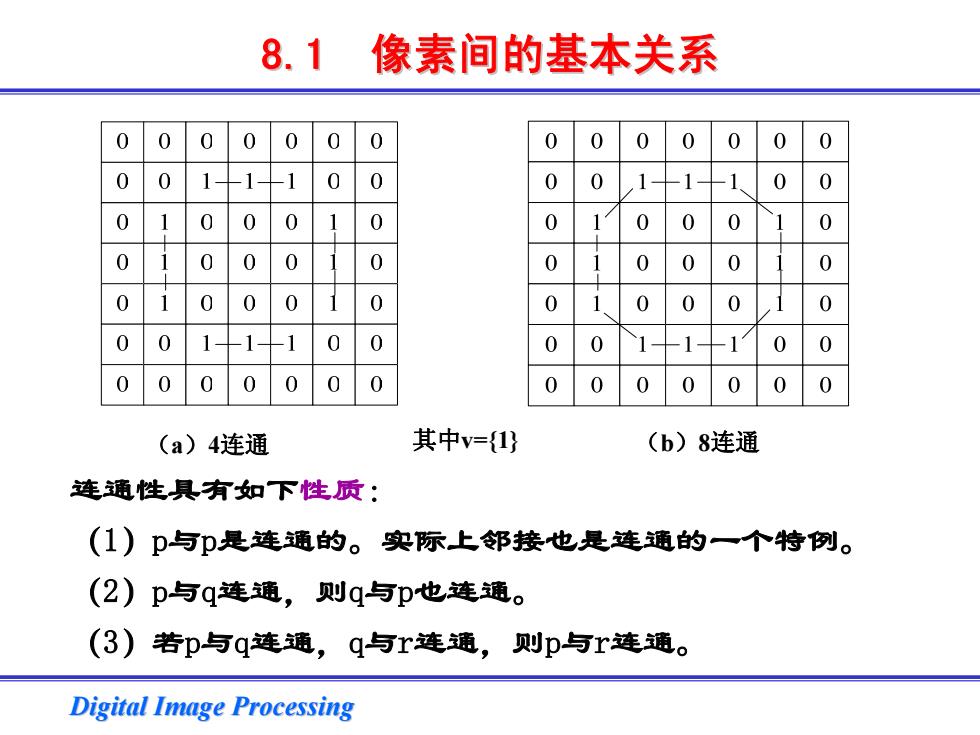
8.1 像素间的基本关系 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (a)4连通 其中v={1} (b)8连通 连通性具有如下性质: (I)p与p是连通的。实际上邻接也是连通的一个特例。 (2)p与q连通,则q与p也连通。 (3)若p与q连通,q与r连通,则p与r连通。 Digital Image Processing
Digital Image Processing Digital Image Processing 连通性具有如下性质: (1)p与p是连通的。实际上邻接也是连通的一个特例。 (2)p与q连通,则q与p也连通。 (3)若p与q连通,q与r连通,则p与r连通。 (a)4连通 其中v={1} (b)8连通 8.1 像素间的基本关系 像素间的基本关系

8.1 像素间的基本关系 区域和边界 1、区域:连通性作为像素间关系中一个基本概念,由此可得 到区域、边界等许多重要概念。对于S中的任一像秦点,S中所 有的与连通的点的集合称为S的连通分量,即一个连通的区 域。 2、边界:设图像中目标点(右图中以1表 0 示)的集合为S,其余点(右图中以0表示)的 集合为SC,则SC称为S的补集。如果目 标S中的点p有相邻点在SC中,那么p就称 为S的边界点,其集合称为S的边界,记 为S'。S中除去S的点,即S一S”称为 0 S的内部。 利用相邻、连通性和边界点可以定义如下一些图像的特征点和线。 Digital Image Processing
Digital Image Processing Digital Image Processing ◘区域和边界 1、区域 :连通性作为像素间关系中一个基本概念,由此可得 到区域、边界等许多重要概念。对于S中的任一像素点p,S中所 有的与p连通的点的集合称为S的连通分量,即一个连通的区 域。 8.1 像素间的基本关系 像素间的基本关系 2、边界 :设图像中目标点(右图中以1表 示)的集合为S,其余点(右图中以0表示)的 集合为 ,则 称为S的补集。如果目 标S中的点p有相邻点在 中,那么p就称 为S的边界点,其集合称为S的边界,记 为 。S中除去 的点,即 称为 S的内部。 C S C S C S S′ S′ S S − ′ 利用相邻、连通性和边界点可以定义如下一些图像的特征点和线
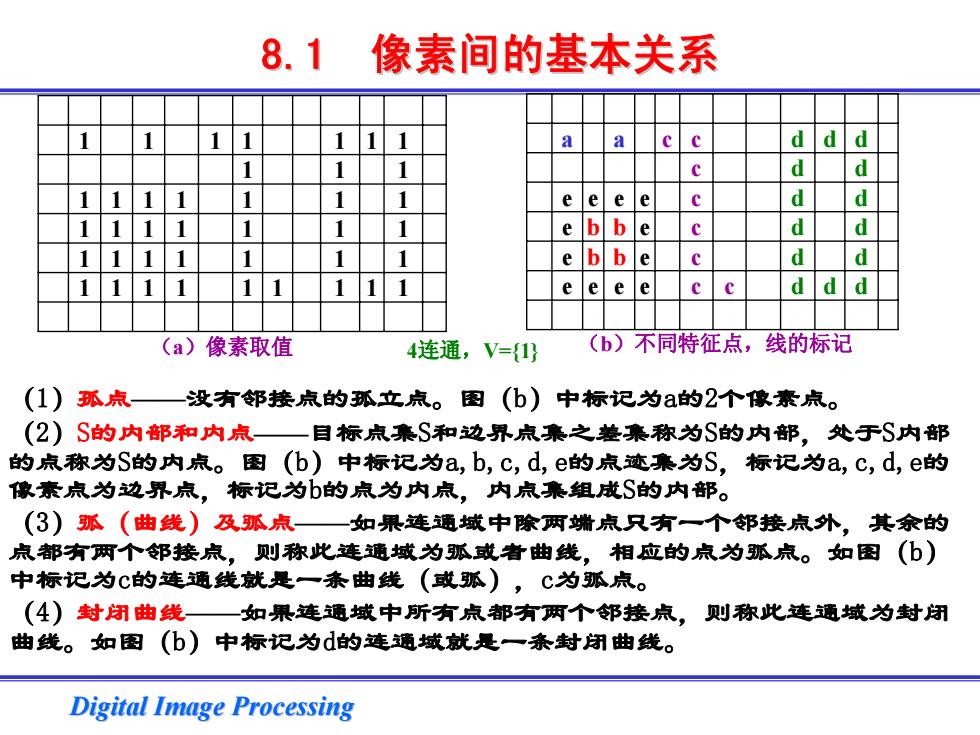
8.1像素间的基本关系 a a d d d d eeee d ebbe d e bbe d (a)像素取值 4连通,V={1 (b)不同特征点,线的标记 (I)孤点—没有邻接点的孤立点。图(b)中标记为a的2个像素点。 (2)S的内部和内点一目标点集S和边界点集之差集称为S的内部,处于S内部 的点称为S的内点。图(b)中标记为a,b,c,d,e的点迹集为S,标记为a,c,d,e的 像素点为边界点,标记为b的点为内点,内点集组成S的内部。 (3)弧(曲线)及孤点—如果连通城中除两端点只有一个邻接点外,其余的 点都有两个邻接点,则称此连通域为弧或者曲线,相应的点为弧点。如图(b) 中标记为C的连通线就是一条曲线(或弧),C为弧点。 (4)封闭曲线—如果连通域中所有点都有两个邻接点,则称此连通城为封闭 曲线。如图(b)中标记为d的连通域就是一条封闭曲线。 Digital Image Processing
Digital Image Processing Digital Image Processing 1 1 11 111 1 11 1111 1 1 1 1111 1 1 1 1111 1 1 1 1111 11 111 a a c c ddd c d d eeee c d d e b b e c d d e b b e c d d eeee c c ddd (a)像素取值 (b)不同特征点,线的标记 8.1 像素间的基本关系 像素间的基本关系 4连通,V={1} (1)孤点——没有邻接点的孤立点。图(b)中标记为a的2个像素点。 (2)S的内部和内点——目标点集S和边界点集之差集称为S的内部,处于S内部 的点称为S的内点。图(b)中标记为a,b,c,d,e的点迹集为S,标记为a,c,d,e的 像素点为边界点,标记为b的点为内点,内点集组成S的内部。 (3)弧(曲线)及弧点——如果连通域中除两端点只有一个邻接点外,其余的 点都有两个邻接点,则称此连通域为弧或者曲线,相应的点为弧点。如图(b) 中标记为c的连通线就是一条曲线(或弧),c为弧点。 (4)封闭曲线——如果连通域中所有点都有两个邻接点,则称此连通域为封闭 曲线。如图(b)中标记为d的连通域就是一条封闭曲线