
1966 ab FIGURE 10.12 Diagonal edge detection. (a)Result of using the mask in Fig.10.9(c. (b)Result of using the mask in Fig.10.9(d).The input in both cases was Fig.10.11(a)
STC b)局部微分算子:二阶微分,用拉普拉斯算子计算 1966 ■特点:常数部分为零;拉普拉斯算子的结果在亮的一边是正的,在暗的 一边是负的。 ■用途:二次导数的符号用于确定像素是在亮的一边,还是暗的一边;0跨 越(零交叉),确定边的准确位置。 0 -1 0 Z 13 -1 6 0 二维函数fx,y)的拉普拉斯算子定义为: V2f=82f/0x2+o2f/0y2 对3x3区域,经验上被推荐最多的形式是: V2f=4zs-(亿+Z4+Z6+Z3)
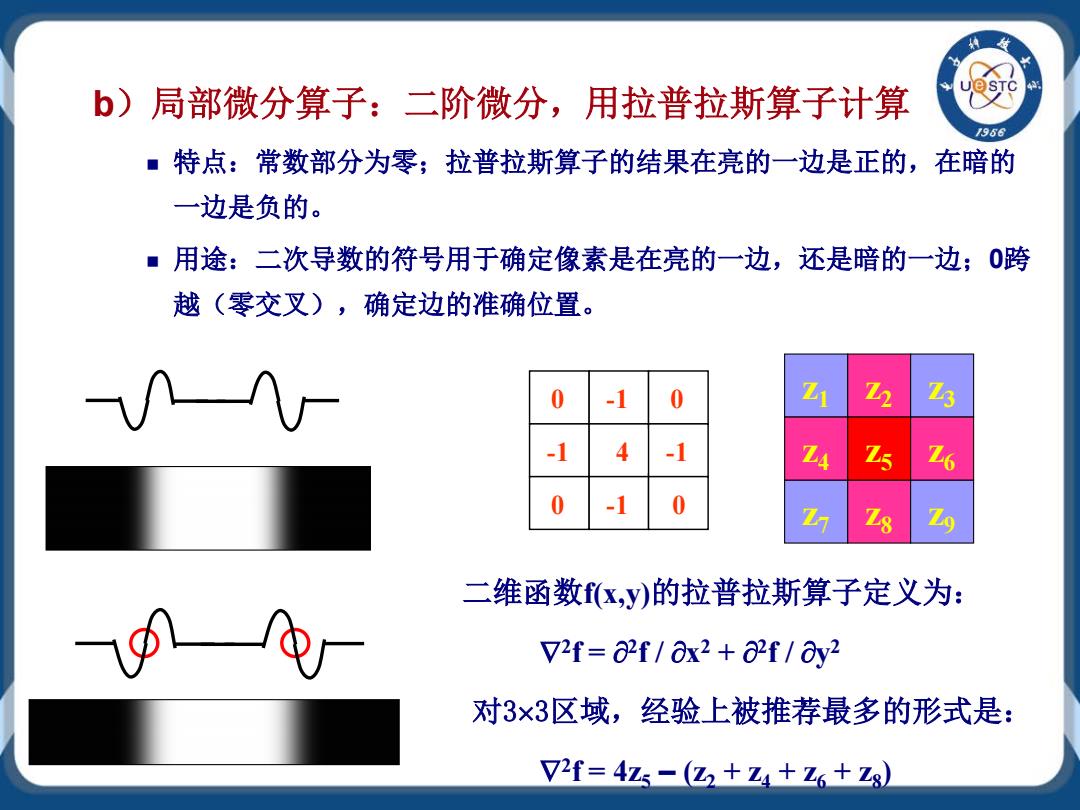
b)局部微分算子:二阶微分,用拉普拉斯算子计算 特点:常数部分为零;拉普拉斯算子的结果在亮的一边是正的,在暗的 一边是负的。 用途:二次导数的符号用于确定像素是在亮的一边,还是暗的一边;0跨 越(零交叉),确定边的准确位置。 0 -1 -1 4 0 -1 0 -1 0 z2 z8 z5 z3 z9 z6 z1 z7 z4 二维函数f(x,y)的拉普拉斯算子定义为: ∇2f = ∂2f / ∂x2 + ∂2f / ∂y2 对3×3区域,经验上被推荐最多的形式是: ∇2f = 4z5 – (z2 + z4 + z6 + z8)

更先进的边缘检测算子: /966 a)马尔(Marr)算子V2h: 定义2-D高斯函数h(x,y): .)-e 其中σ是高斯分布的均方差。如果令2=x2+y2,那么根 据求拉普拉斯的定义式,有 m-(。) 马尔(Marr)算子V2h通常称为高斯型的拉普拉斯算子 (Laplacian of a Gaussian,LoG)
a) 马尔(Marr)算子▽2h : 定义2-D高斯函数h(x,y): ( ) σ + = − 2 2 2 2 x y h x,y exp 其中σ是高斯分布的均方差。如果令r2=x2+y2 , 那么根 据求拉普拉斯的定义式,有 σ − σ − σ ∇ = − 2 2 4 2 2 2 2 r exp r h 马尔(Marr)算子▽2h通常称为高斯型的拉普拉斯算子 (Laplacian of a Gaussian, LoG)。 更先进的边缘检测算子:
v 是一个轴对称函数: 72h 由图可见,这个函数 在=士c处有过零点,在 |r<c时为正,在|r>o 时为负。 由于图像的形状,马尔算子有时被称为墨西哥草帽函数。 用V对图像做卷积,等价于先对图像做高斯平滑,然后再用V2对 图像做卷积。 因为V2的平滑性质能减少噪声的影响,所以当边缘模糊或噪声较 大时,利用Vh检测过零点能提供较可靠的边缘位置
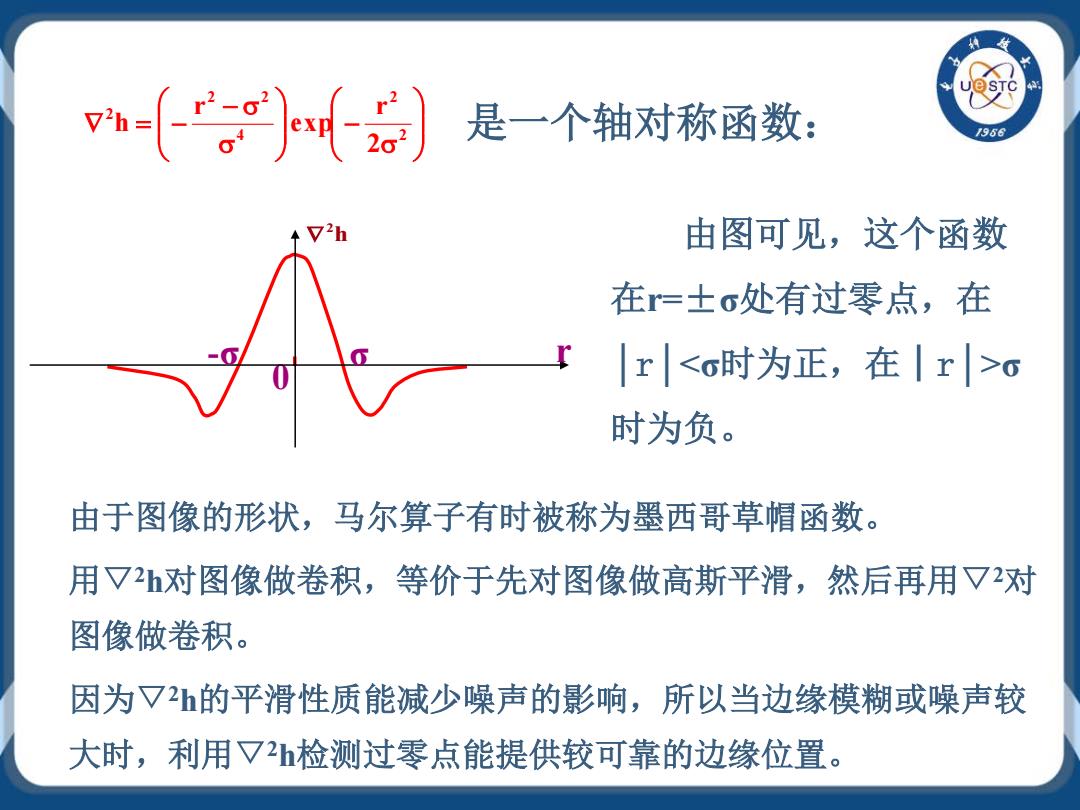
是一个轴对称函数: 由图可见,这个函数 在r=±σ处有过零点,在 │r│<σ时为正,在│r│>σ 时为负。 σ − σ − σ ∇ = − 2 2 4 2 2 2 2 r exp r h 0 -σ σ r h 2 ∇ 由于图像的形状,马尔算子有时被称为墨西哥草帽函数。 用▽2h对图像做卷积,等价于先对图像做高斯平滑,然后再用▽2对 图像做卷积。 因为▽2h的平滑性质能减少噪声的影响,所以当边缘模糊或噪声较 大时,利用▽2h检测过零点能提供较可靠的边缘位置
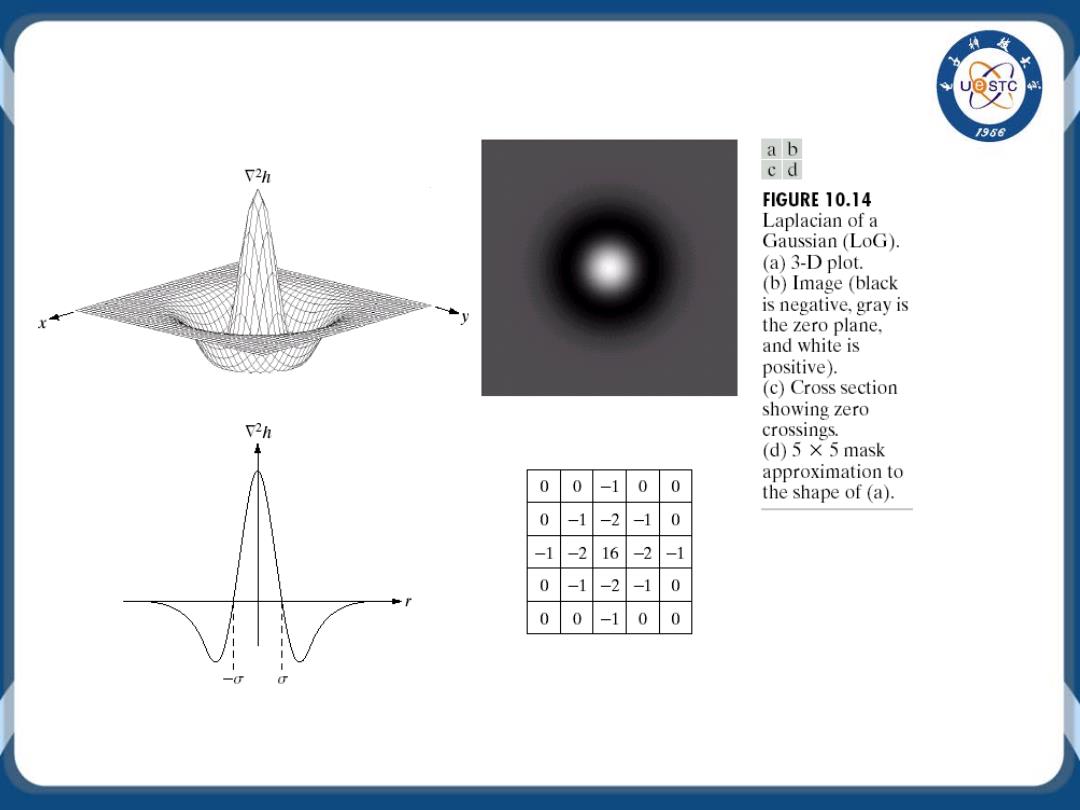
1956 ab V2h FIGURE 10.14 Laplacian of a Gaussian (LoG). (a)3-D plot. (b)Image (black is negative,gray is the zero plane, and white is positive). (c)Cross section showing zero T2h crossings. (d)5×5mask approximation to 0 0 0 the shape of (a). -2 0 16 -2 -1 -2 0 0 0 0 0