
4 由上图我们可以得出结论:一阶导数可以用 /966 于检测图像中的一个点是否是边缘点。同样,二 阶导数的符号可以用于判断一个边缘像素是在边 缘亮的一边还是在暗的一边。 注意:围绕一条边缘,二阶导数的两条附加性质: 1)对图像中的每条边缘,二阶导数生成两个值 (这是一个不希望得到的特点)。2)一条连接二 阶导数正极值和负极值的虚线将在边缘中点有过 零点
由上图我们可以得出结论:一阶导数可以用 于检测图像中的一个点是否是边缘点。同样,二 阶导数的符号可以用于判断一个边缘像素是在边 缘亮的一边还是在暗的一边。 注意:围绕一条边缘,二阶导数的两条附加性质: 1)对图像中的每条边缘,二阶导数生成两个值 (这是一个不希望得到的特点)。2)一条连接二 阶导数正极值和负极值的虚线将在边缘中点有过 零点

1956 A W FIGURE 10.7 First column:images and gray-level profiles of a ramp edge corrupted by a random Gaussian noise of mean 0 and 0.0.0.1,1.0.and 10.0,respectively.Second col- b umn:first-derivative images and gray-level profiles.Third column:second-derivative images and gray-level profiles. d Tm阿
17
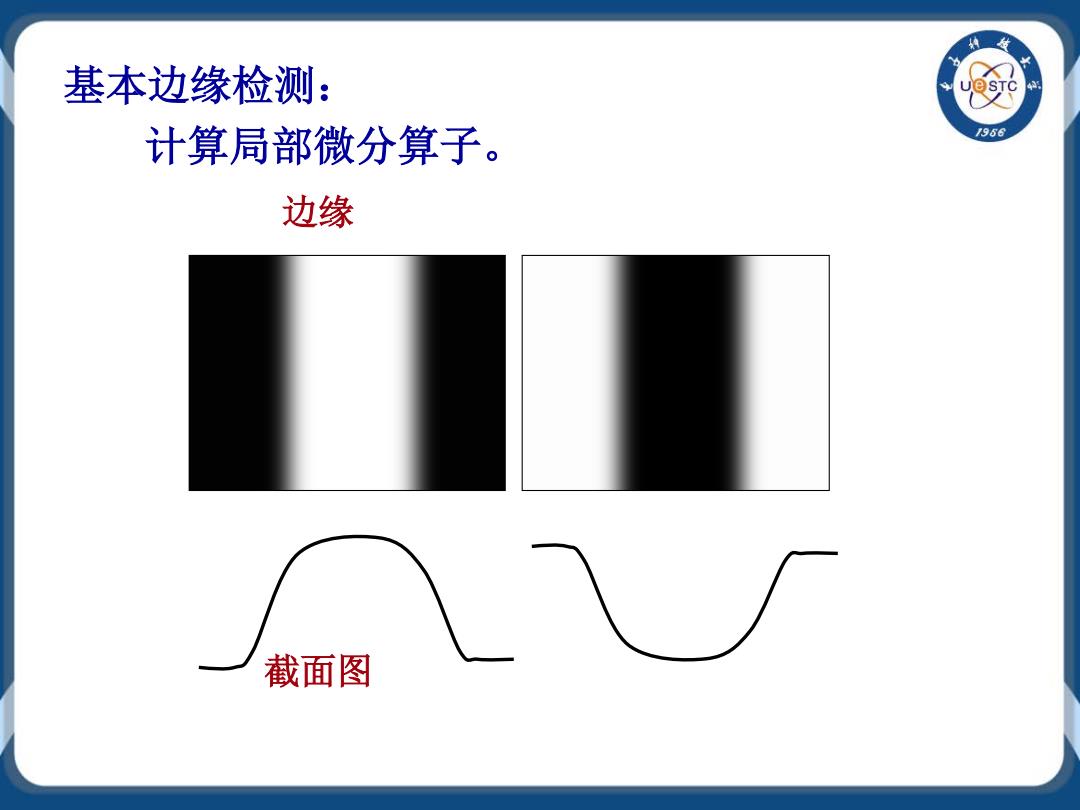
基本边缘检测: 计算局部微分算子。 1956 边缘 截面图
基本边缘检测: 计算局部微分算子。 截面图 边缘

a)局部微分算子:一阶微分,用梯度算子计算 ·特点:常数部分为零;左图中左侧的边是正的(由暗到 亮),右侧的边是负的(由亮到暗);右图结论相反。 ·用途:用于检测图像中边的存在
a)局部微分算子:一阶微分,用梯度算子计算 • 特点:常数部分为零;左图中左侧的边是正的(由暗到 亮),右侧的边是负的(由亮到暗);右图结论相反。 • 用途:用于检测图像中边的存在

梯度算子(Gradient operators) /966 函数fx,y)在K,y)处的梯度为一个向量: Vf=[of ox,of ay] 计算这个向量的大小为: IVf mag(Vf)=[(of ax)2+(of ay)2]12 近似为:IVf≈Gxl+|GyI 梯度的方向角为:o(k,y)=arctan(Gy/Gx)
梯度算子(Gradient operators) 函数f(x,y)在(x,y)处的梯度为一个向量: ∇f = [∂f / ∂x , ∂f / ∂y]T 计算这个向量的大小为: |∇f| = mag(∇f ) = [(∂f / ∂x)2 +(∂f / ∂y)2]1/2 近似为: |∇f| ≈ |Gx| + | Gy | 梯度的方向角为:α(x,y) = arctan(Gy / Gx)