南京大学：《并行处理技术——分布式与并行计算 Distributed and Parallel computing（并行计算——结构、算法、编程）》课程教学资源（课件讲稿）第九章 并行数值算法（稠密矩阵运算）

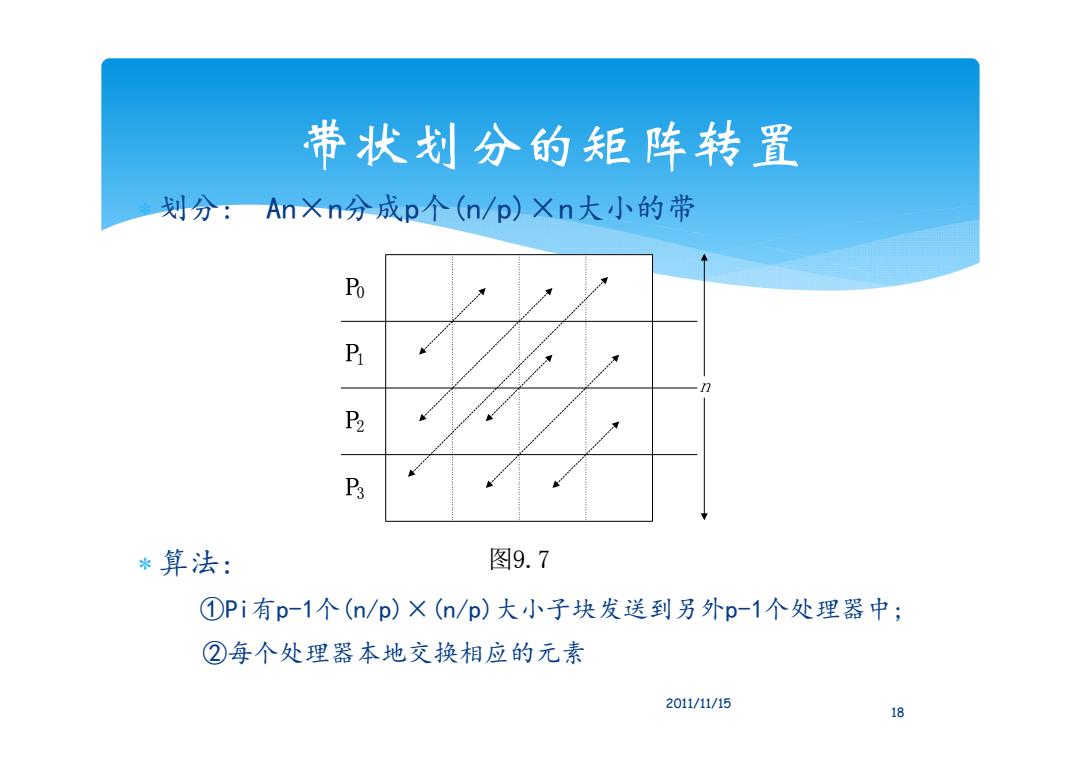
带状划分的矩阵转置 划分：AnXn分成p个(n/p)×n大小的带 Po P P2 P3 *算法： 图9.7 ①Pi有p-1个(n/p)X(n/p)大小子块发送到另外p-1个处理器中； ②每个处理器本地交换相应的元素 2011/11/15 18

带状划分的矩阵转置  划分: An×n分成p个(n/p)×n大小的带  算法: ①Pi有p-1个(n/p)×(n/p)大小子块发送到另外p-1个处理器中; ②每个处理器本地交换相应的元素 图9.7 0 1 2 3 18 2011/11/15

第九章稠密矩阵运算 9.1矩阵的划分 92矩阵转置 93矩阵-向量乘法 9.4矩阵乘法

第九章 稠密矩阵运算 9.1 矩阵的划分 9.2 矩阵转置 9.3 矩阵 ‐向量乘法 9.4 矩阵乘法

单处理机上的矩阵-向量乘法 算法92单处理机上的矩阵-向量乘法 米 输入：Anxn,Xnx1 米 输出：Ynx1 Begin for i=o to n-1 do Yi=0 for j=o to n-1 do yi=yi+aijxxj endfor endfor End *算法运行时间为0(n2) 20 2011/11/15

 算法9.2单处理机上的矩阵‐向量乘法  输入：ܣ௡ൈ௡，ܺ௡ൈଵ  输出： ܻ௡ൈଵ Begin for i=0 to n‐1 do ݕ ௜ൌ 0 for j=0 to n‐1 do ௝ݔ ൈ௜ ൅ ܽ௜,௝ ݕ ൌ௜ ݕ endfor endfor End  算法运行时间为ܱሺ݊ଶሻ 20 2011/11/15 单处理机上的矩阵‐向量乘法

93矩阵-向量乘法 931带状划分的矩阵-向量乘法 932棋盘划分的矩阵-向量乘法

9.3 矩阵 ‐向量乘法 9.3.1 带状划分的矩阵 ‐向量乘法 9.3.2 棋盘划分的矩阵 ‐向量乘法

带状划分的矩阵-向量乘法 划分（行带状划分：P存放X和a.o,a,…,an-l并输出y *算法：对p=n情形 ①每个P向其他处理器播送X(多到多播送) ②每个P计算； *注：对p<n情形，算法中P要播送X中相应的n/p个分量 ()超立方连接的计算时间 T。=+1,logp+”1,(p-)∥前1项是乘法时间，后2项是多到多的播送时间 n =一+t,logp+t。∥p充分大时 (2)网孔连接的计算时间 T,=”+2(VD-以，+”1，(p-)∥前1项是乘法时间，后2项是多到多的播送时间 +2,(VD-)+m.∥p充分大时 n 2011/11/15 22

带状划分的矩阵 ‐向量乘法  划分(行带状划分): Pi存放xi和ai,0,ai,1,…,ai,n-1, 并输出yi  算法: 对p=n情形 ①每个Pi向其他处理器播送xi(多到多播送)； ②每个Pi计算；  注: 对p<n情形,算法中Pi要播送X中相应的n/p个分量 (1)超立方连接的计算时间 (2)网孔连接的计算时间 充分大时 前 项是乘法时间， 后 项是多到多的播送时间 t p nt p p n t p p n t p p n T s w p s w log // log ( 1) // 1 2 2 2        22 2011/11/15 充分大时 前 项是乘法时间， 后 项是多到多的播送时间 t p nt p p n t p p n p t p n T s w p s w 2 ( 1) // 2( 1) ( 1) // 1 2 2 2         