
第二篇并行算法的设计 Case Study 1.求取最大值算法 2.计算前缀和算法
第二篇 并行算法的设计 Case Study 1.求取最大值算法 2.计算前缀和算法
求取最大值 令n=2m,A是一个2维的数 组,待求最大值的n个数开 始存放在A(n),A(n+1),, K=0 A(2n-1),所求得的最大值 置于A(1)中。 sss--- An2-1 K=m-2 /2 ----D An-l K=m-1 n/2+1 n-2 n/2. A An+2 -“A20-4 A2n-3A2n-2 A2n-1 3 2011/9/27
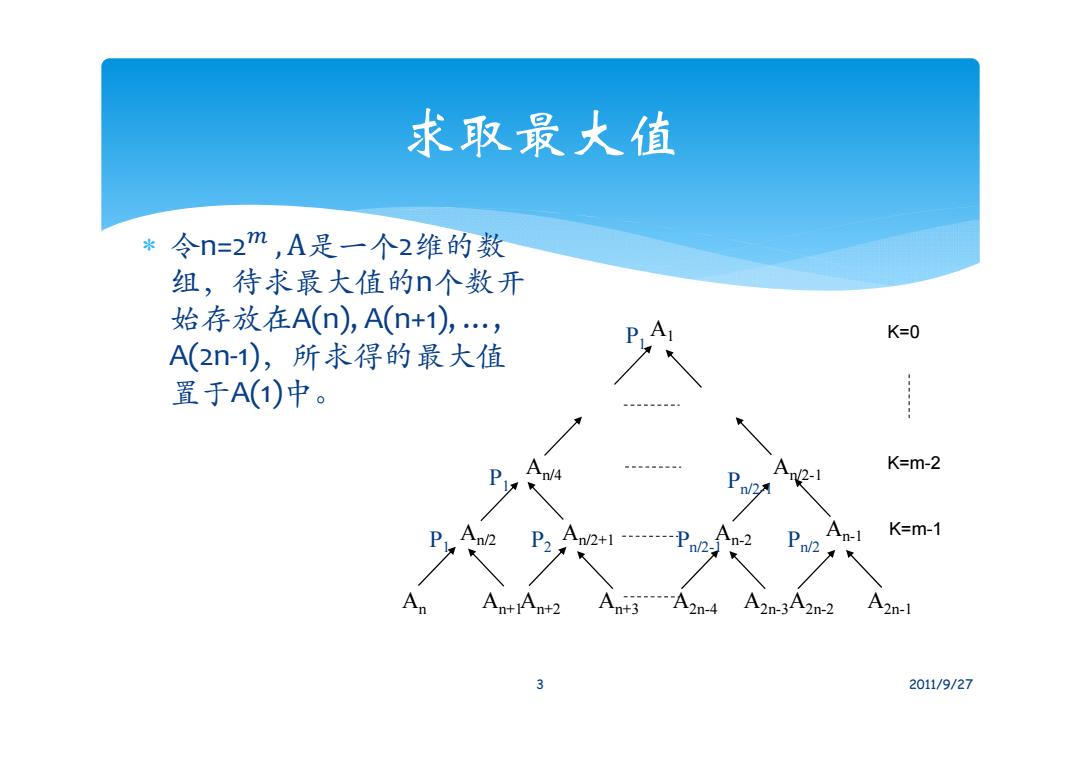
令n=2 , A是一个2维的数 组,待求最大值的n个数开 始存放在A(n), A(n+1), …, A(2n‐1),所求得的最大值 置于A(1)中。 求取最大值 3 2011/9/27 A1 An/4 An/2-1 An/2 An/2+1 An-2 An-1 An An+1An+2 An+3 A2n-4 A2n-3A2n-2 A2n-1 K=m-1 K=m-2 P K=0 1 P1 P2 Pn/2-1 Pn/2 P1 Pn/2-1

求最大值 算法4.1:SMD-TCSM①上求最大值算法 输入:n=2m个数存放在A(n,2n-1)中; 输出:求得的最大值置于A(1)中。 Begin for k=m-1 to o do for j=2k to 2k+1-1 par-do A[j]=max{A[2j],A[2j+1]} end for end for end *时间分析 算法的时间:t(n)=m×O(1)=O(Iogn); 总比较次数:O(n); 最大的处理器数:p(n)=n/2 2011/9/27 4
求最大值 算法4.1: SIMD-TC(SM)上求最大值算法 输入: n=2݉ 个数存放在A(n,2n-1)中; 输出:求得的最大值置于A(1)中。 Begin for k=m‐1 to 0 do for j=2k to 2k+1‐1 par‐do A[j]=max{A[2j], A[2j+1]} end for end for end 时间分析 算法的时间:t(n)=m×O(1)=O(logn); 总比较次数:O(n); 最大的处理器数:p(n)=n/2 4 2011/9/27

计算前缀和 问题定义 n个元素{区1,X2,…x},前缀和是n个部分和: S=x1*x2*.*x,1≤i≤n这里*可以是十或X *串行算法:S=S-x 计算时间为On) *并行算法:SMD-TC上非递归算法 令A0=x,i=1~n, Bh,j1和Ch,i]为辅助数组h=0~logn,jF1~n/2) 数组B记录由叶到根正向遍历树中各结,点的信息(求和) 数组C记录由根到叶反向遍历树中各结,点的信息(播送前 缀和) 2011/9/27 5
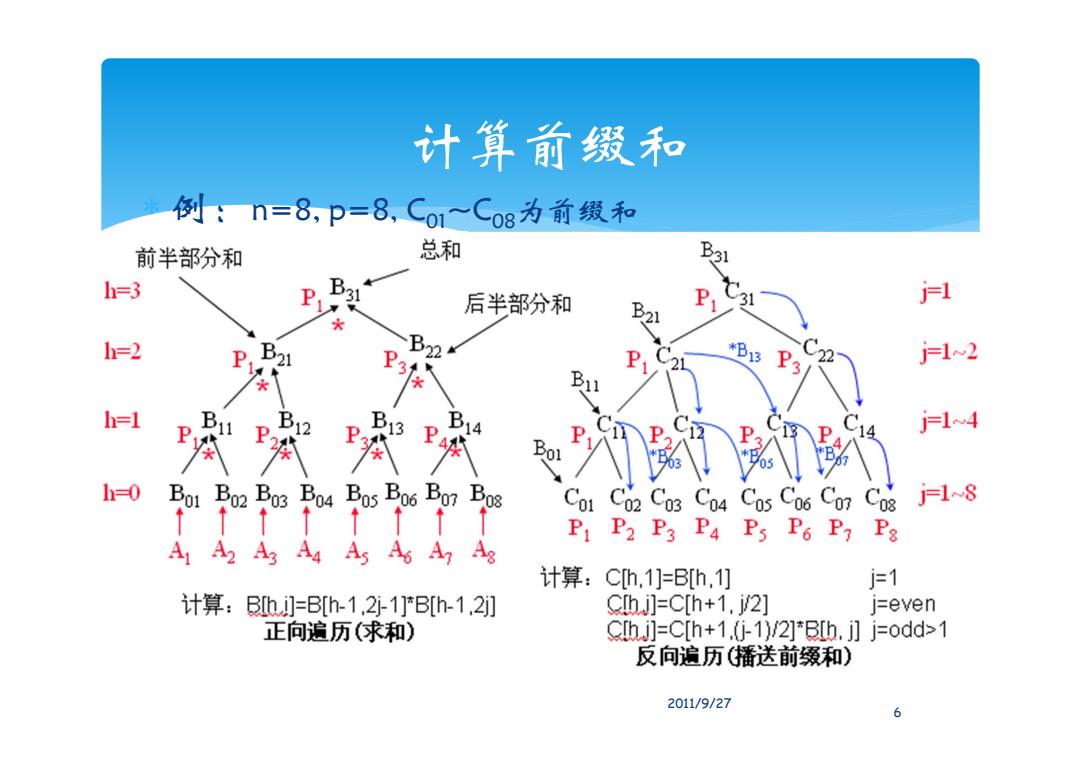
计算前缀和 问题定义 n个元素{x1,x2,…,xn},前缀和是n个部分和: Si=x1*x2*…*xi, 1≤i≤n 这里*可以是+或× 串行算法: Si=Si-1*xi 计算时间为 O(n) 并行算法:SIMD-TC上非递归算法 令A[i]=xi, i=1~n, B[h,j]和C[h,j]为辅助数组(h=0~logn, j=1~n/2h) 数组B记录由叶到根正向遍历树中各结点的信息(求和) 数组C记录由根到叶反向遍历树中各结点的信息(播送前 缀和) 5 2011/9/27
计算前缀和 例:1=8,p=8,Co1~C08为前缀和 前半部分和 总和 3 h=3 B31 后半部分和 1 B21 P h=2 B2“ 31 *B13P3 22 j=1~2 h=1 2 13 3 B14 j=1~4 h=0 Bo1 B02 B03 B04 Bos Bo6 B07 Bo3 j=18 P1 P2 P3 P4 Ps P6 P7 P8 A1 A2 A3 A4 As A6 A7 Ag 计算:Ch,1]=B[h.1) j=1 计算:B]=B[h-1,21]*B[h-1,2] C[hj]=C[h+1.j/2] =even 正向遍历(求和) C[h j]=C[h+1.(j-1)/2]*B[h.j]j=odd>1 反向遍历(播送前缀和) 2011/9/27 6
计算前缀和 例:n=8, p=8, C01‾C08为前缀和 6 2011/9/27