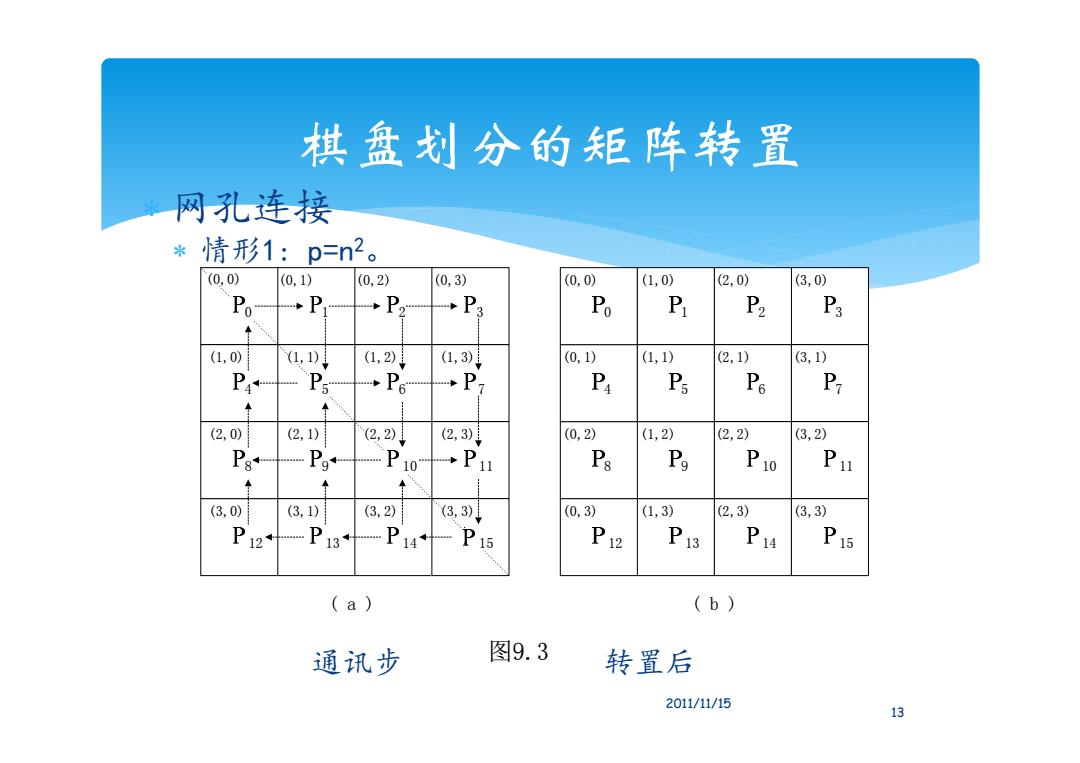
棋盘划分的矩阵转置 网孔连接 情形1:p=n2。 (0,0) (0,1) (0,2) (0,3) (0,0) (1,0) (2,0) (3,0) Po →P2 →P3 Po P P2 P3 (1,0) (1,0 (1,2)↓ (1,3) (0,1) (1,1) (2,1) (3,1) P+ →P6 →P7 P P Po P (2,0) (2,1) (2,2) (2,3)月 (0,2) (1,2) (2,2) (3,2) Pa+ P9P10 →P Ps Pa P10 Pu (3,0) (3,1) (3,2) (3,3 (0,3) (1,3) (2,3) (3,3) P14 P15 P1 P13 P14 P15 (a) (b) 通讯步 图9.3 转置后 2011/11/15 13
棋盘划分的矩阵转置 网孔连接 情形1: p=n 2 。 通讯步 转置后 (3,0) (1,0) (1,2) (1,3) (2,0) (2,1) (2,3) (3,1) (3,2) ( a ) ( b ) 图9.3 (0,0) (0,1) (0,2) (0,3) (1,0) (1,1) (1,2) (1,3) (2,0) (2,1) (2,2) (2,3) (3,0) (3,1) (3,2) (3,3) (0,0) (0,1) (0,2) (0,3) (1,1) (2,2) (3,3) 3 7 11 15 2 6 10 14 1 5 9 12 13 0 4 8 3 7 11 15 2 6 14 10 1 9 13 5 12 4 8 0 13 2011/11/15
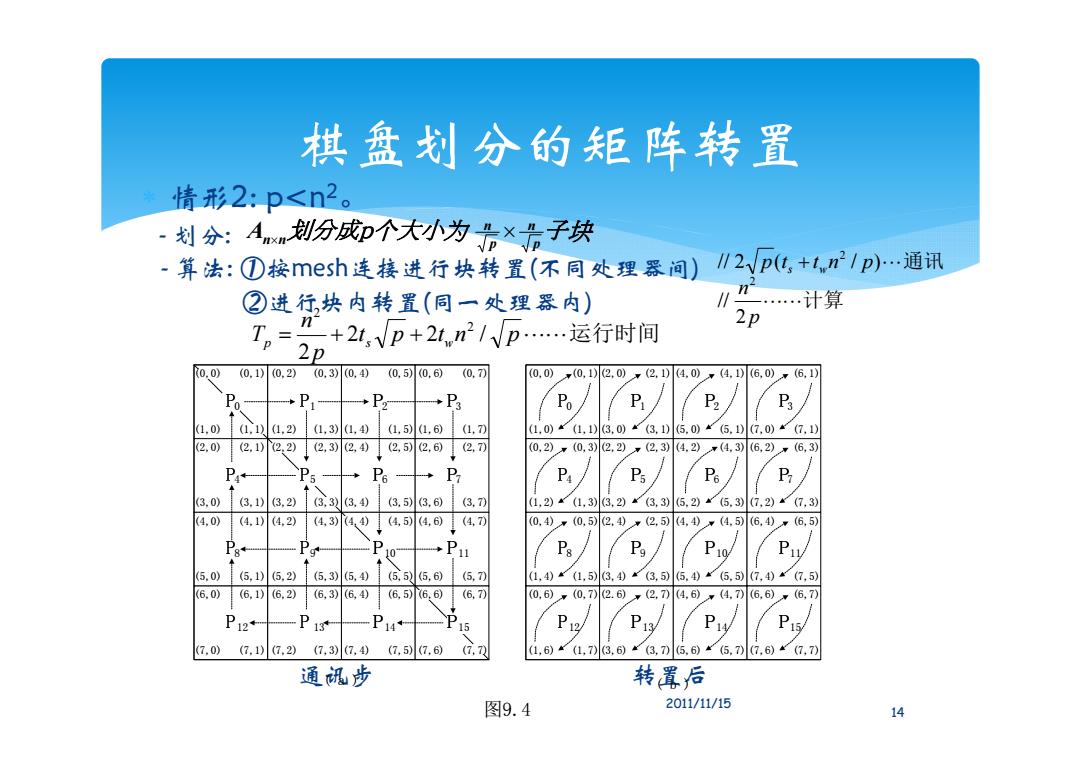
棋盘刻分的矩阵转置 情形2:p<n2。 -划分:Am划份成D个大小为是×北子块 -算法:①按mesh连接进行块转置(不同处理器间)∥2√p,+1,n/p)…通讯 ②进行块内转置(同一处理器内) .…计算 2p T。=+24,Np+21,/D…运行时间 0.0) (0.1)0,2)(0,3)0,4) (0.5)0,6) (0.7) 0,0)(0,1)2,0),(2,1D4.0),(4,6,0)(6,1) P +P1 →Pz →P3 Po P P P 1.0)(①,11,2)1,3)1,4)(1,51,6)(1,7 (1,0)k(1,1)3,0)(3.1)5.0)(5.1D7,0)(7,1) (2.0)1 (2.1)2.2)(2,3)2,4)(2,5)2.6)(2,7) (0,2),(0,3)2.2)x(2,34.2)m4,3)6,2)(6,3) P+ P6 P P P Pe P 3.0)(3.1)3,2) (3,33.4)(3.53.6)(3.70 (1,2)(1,3)3,2)(3,3)5.2)(5.3)(7,2)(7,3) (4.0) (4.1)(4.2) (4,3)4、4)(4,5)(4,6)(4,7) 0,4)(0,52,4)¥(2,54,4)(4,5 (6.4)x(6,5) Pa+ →P1 Ps Pa P10 P/ (5.0)(5,105,2) (5.3)5,4)(⑤55,6)(5,7) (1,4)r(1,53.4)(3,55.40 (5.5)(7,4)(7,5) (6.0) (6.1)6,2)(6,3)6,4) (6,5)6,6)(6,7) (0,6)(0,7)2.6)(2,7)4,6)¥(4,7)6,6)(6,7) P12 P13 P14 P13 P15/ 《7,0) (7,1)(7,2) (7,3)7,40 (7,57,6)(,70 (1,6)(1,7)3,6)(3,75.6) (5,707,6)4(7,7) 通讯步 转置后 图9.4 2011/11/15 14
棋盘划分的矩阵转置 情形2: p<n 2 。 - 划分: - 算法: ①按mesh连接进行块转置(不同处理器间) ②进行块内转置(同一处理器内) 通讯步 转置后( b ) ( a ) 图9.4 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15 (0,0) (1,0) (0,2) (1,2) (1,4) (0,4) (1,6) (0,6) (0,1) (1,1) (0,3) (1,3) (1,5) (0,5) (1,7) (0,7) (2,0) (3,0) (2,2) (3,2) (3,4) (2,4) (3,6) (2.6) (2,1) (3,1) (2,3) (3,3) (3,5) (2,5) (3,7) (2,7) (4,0) (5,0) (4,2) (5,2) (5,4) (4,4) (5,6) (4,6) (4,1) (5,1) (4,3) (5,3) (5,5) (4,5) (5,7) (4,7) (6,0) (7,0) (6,2) (7,2) (7,4) (6,4) (7,6) (6,6) (6,1) (7,1) (6,3) (7,3) (7,5) (6,5) (7,7) (6,7) 4 8 12 0 1 5 9 13 2 6 10 14 3 7 11 15 (1,0) (2,0) (3,0) (5,0) (4,0) (7,0) (6,0) (0,0) (0,1) (1,1) (2,1) (3,1) (5,1) (4,1) (7,1) (6,1) (0,2) (1,2) (2,2) (3,2) (5,2) (4,2) (7,2) (6,2) (0,3) (1,3) (2,3) (3,3) (5,3) (4,3) (7,3) (6,3) (0,4) (1,4) (2,4) (3,4) (5,4) (4,4) (7,4) (6,4) (0,5) (1,5) (2,5) (3,5) (5,5) (4,5) (7,5) (6,5) (0,6) (1,6) (2,6) (3,6) (5,6) (4,6) (7,6) (6,6) (0,7) (1,7) (2,7) (3,7) (5,7) (4,7) (7,7) (6,7) 14 2011/11/15 A n n 划分成p个大小为 n p n p 子块 // 2 p(ts tw n2 / p)通讯 计算 p n 2 // 2 t p t n p 运行时间 p n Tp s w 2 2 / 2 2 2

棋盘划分的矩阵转置 *超立方连接 *划分:Am别份成知个大小为北×光子块 *算法: ①将A= A: ②对A递归应用①进行转置,直至分块矩阵的元素处于同一处理器; ③进行同一处理器的内部转置。 *运行时间: n)log√p ∥内部转置分选路:2(,+,递归步:l0gD 2p p 2p +i,+l. 2P ogP 2011/11/15 15
棋盘划分的矩阵转置 超立方连接 划分: 算法: ① ②对Aij递归应用①进行转置,直至分块矩阵的元素处于同一处理器; ③进行同一处理器的内部转置。 运行时间: 15 2011/11/15 A n n 划分成p个大小为 n p n p 子块 p p n t t p n p p n t t p n p p n t t p n T s w p s w s w )log 2 2 ) log 2 2 )log // 2 2 2 2 2 2 2 ( ( 内部转置 ,选路: ( ,递归步: 12 22 11 21 21 22 11 12 A A A A A A A A 将A = 转置为
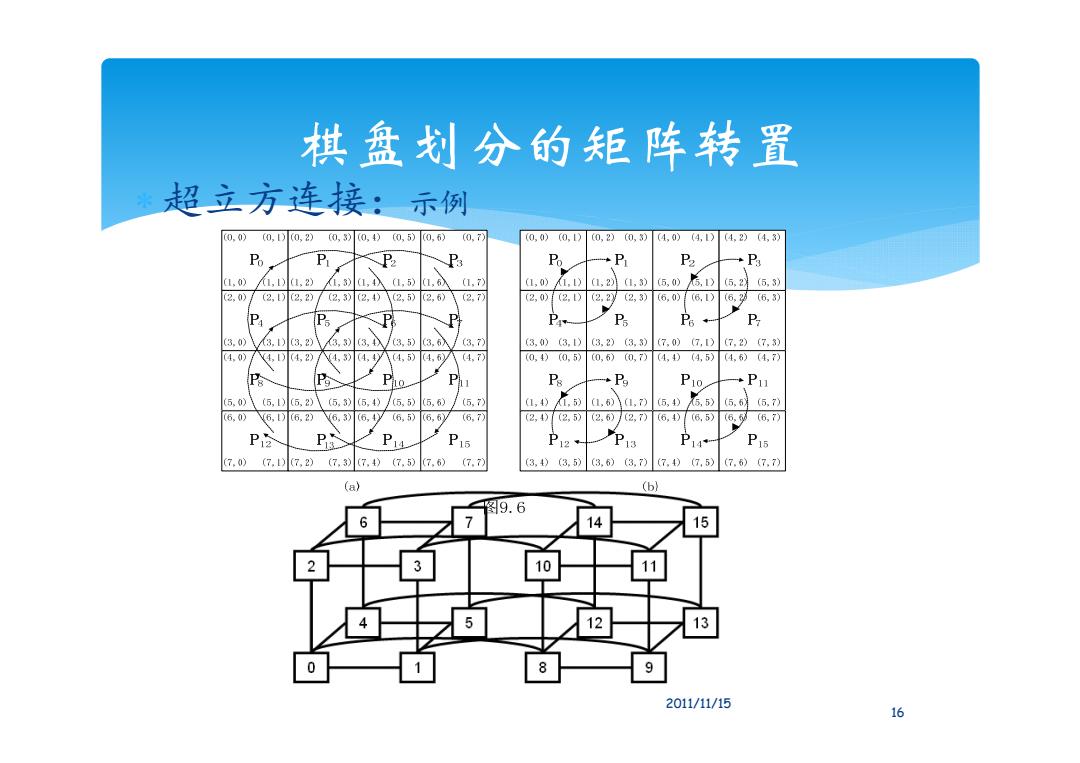
棋盘刻分的矩阵转置 超立方连接:示例 0.0) (0,)0,2)0,3)0,4)0,5)0,6) 0.7 (0,0)(0,D 0,2)0,3) (4.0)(4,1)(4.2)(4,3) Po P B Ps P P P +P3 (1.0)/1,1)1.2) 1,3)1,4入(1,5)1.6 1.7) (1,0)1.) 1,21,3)6,0后,D5.26.3) (2.0) (2,tD2.2)7(2,3)(2,4)1(2,5)2,6) (2.7) (2,0)(2.1) (2,2y(2,3) (6,00(6.1)(6.2(6,3) P P P P Ps P6+ P 3.0)/8)3,2)\33)3,/3,5)3,入 3.7) (3,0)(3.1)(3.2)(3.3)(7.0)(7,.1) (7.2)(7,3) (4.0)/ 4,)4,2)4,3)(4.4y(4,5)4.6y八(4.7 0,4)0.5) 0,5)0,7)(4,4)(4,5) (4.6)(4,7) P P Pu Ps +P9 P10 +P11 (5,0)(5,1)5,2) (5,3)5,4)/5,5)5,60 /(5,7) a,0,)a,4,)5,9 后) (5,5(5,7) (6,0) 6,1)6.2) V6,3)6,4y(6,5)6,5y (6,7) (2,4)(2,5)(2.6)(2,7)(6,4)6,5)(6.5(6,7) P ?6 P12 P18 卫14 P15 (7.0) (7.)7,2)(7.3)(7.4)(7.5)7.6)(7.7) (3.4)(3.5) (3.6)(3.7)(7,4)(7,5)(7.5)(7.7) (a) (b) 图9.6 6 7 14 15 2 3 57 2 13 07 1 2011/11/15 16
棋盘划分的矩阵转置 超立方连接:示例 16 2011/11/15

9.2矩阵转置 921棋盘划分的矩阵转置 9.2.2带状划分的矩阵转置
9.2 矩阵转置 9.2.1 棋盘划分的矩阵转置 9.2.2 带状划分的矩阵转置