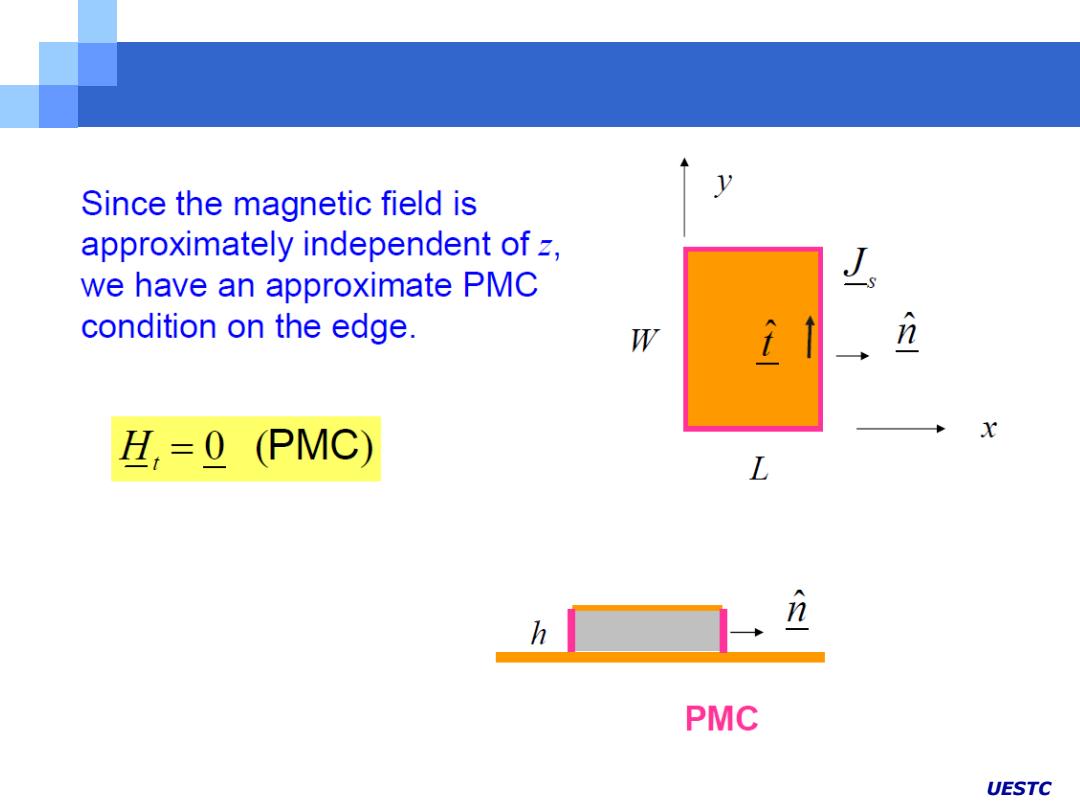
y Since the magnetic field is approximately independent of z, we have an approximate PMC condition on the edge. W n H=0 (PMC) X L n h PMC UESTC
UESTC
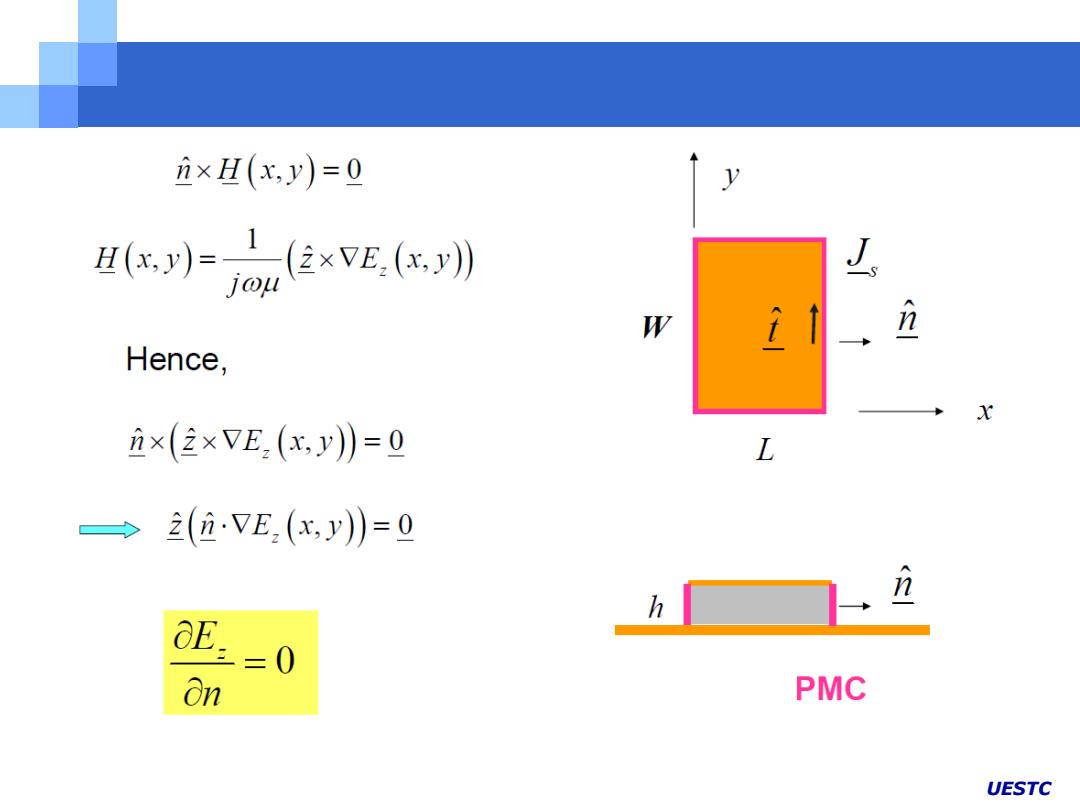
i×H(x,y)=0 y (川=o住xvE.(c》 W n Hence, X i×(2×VE(c,y月=0 L →2(iVE,(x,y)》=0 n h On PMC UESTC
UESTC

分析方法 √传输线法(1D,简单,精度低,只能用于矩形贴片) √腔模理论法(2D,简单,精度适中,适用于规则贴片) √数值方法(3D,复杂,高精度,适用于任意贴片) UESTC
UESTC 分析方法 传输线法(1D,简单,精度低,只能用于矩形贴片) 腔模理论法(2D,简单,精度适中,适用于规则贴片) 数值方法(3D,复杂,高精度,适用于任意贴片)
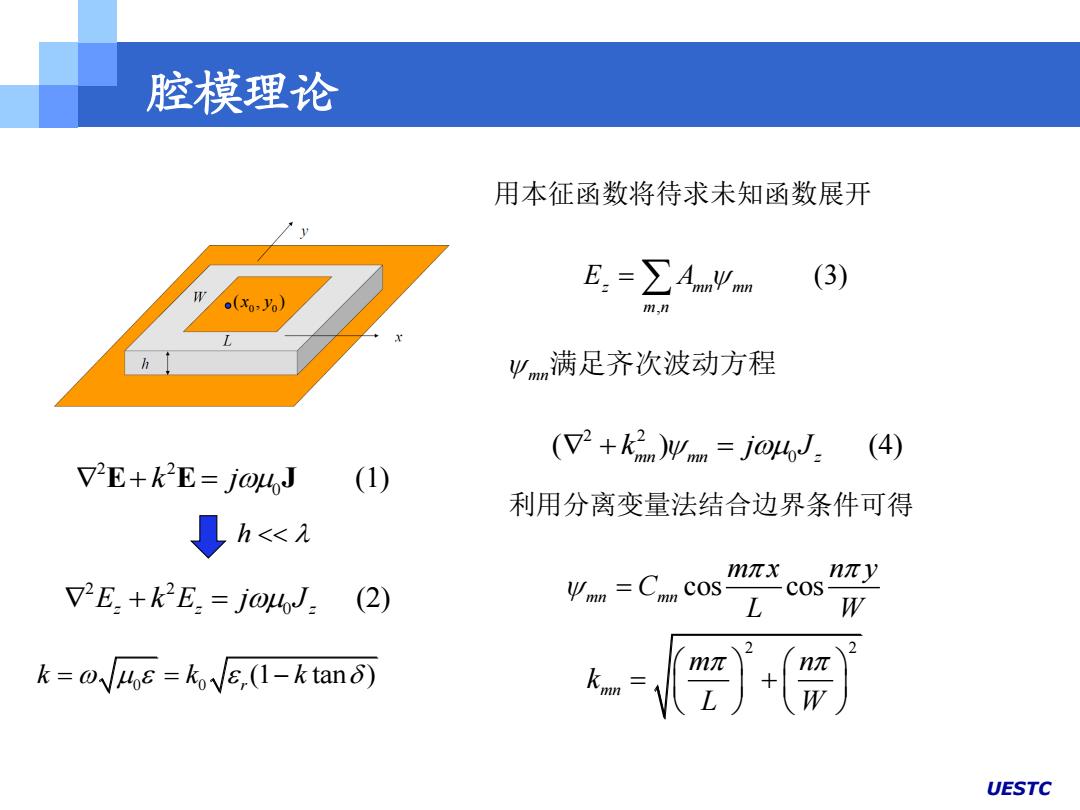
腔模理论 用本征函数将待求未知函数展开 E.=∑Amy mn (3) (xo%) 171,n h 少mm满足齐次波动方程 (2+kir jotoJ (4) E+k2E=jomoJ (1) 利用分离变量法结合边界条件可得 ↓h<元 mπx nπy VE+k2E.=j04J.(2) =Cmn COS L W k=o√4e=koVE,(I-ktanδ) 《】 UESTC
UESTC 2 2 0 E E J k j (1) 2 2 0 (2) E k E j J z z z h 0 0 (1 tan ) r k k k 2 2 0 ( ) (4) mn mn z k j J , (3) z mn mn m n E A 用本征函数将待求未知函数展开 cos cos mn mn m x n y C L W 2 2 mn m n k L W 0 0 ( , ) x y 腔模理论 mn满足齐次波动方程 利用分离变量法结合边界条件可得

将(3)代入(2) ∑An(k2-kru ru=j04J (5) m.n 用wm乘以等式两边,并对空腔区域积分 A(k-∫dv=-jou∫J:。小 (6) m,n 利用本征函数的正交性,即仅当m=m',n=n'时,积分不为零,得 jo4J:"h=jo4(,a) A-花yn本胶-民wva】 (7) UESTC
UESTC 将(3)代入(2) 2 2 0 , ( ) (5) mn mn mn z m n A k k j J * 用 m n' '乘以等式两边,并对空腔区域积分 2 2 * * ' ' 0 ' ' , ( ) (6) mn mn mn m n z m n m n v v A k k dv j J dv 利用本征函数的正交性,即仅当m m n n ', '时,积分不为零,得 * * 0 0 2 2 2 2 * * , = (7) , z mn z mn v mn mn mn mn mn mn mn v j j J dv J A k k k k dv