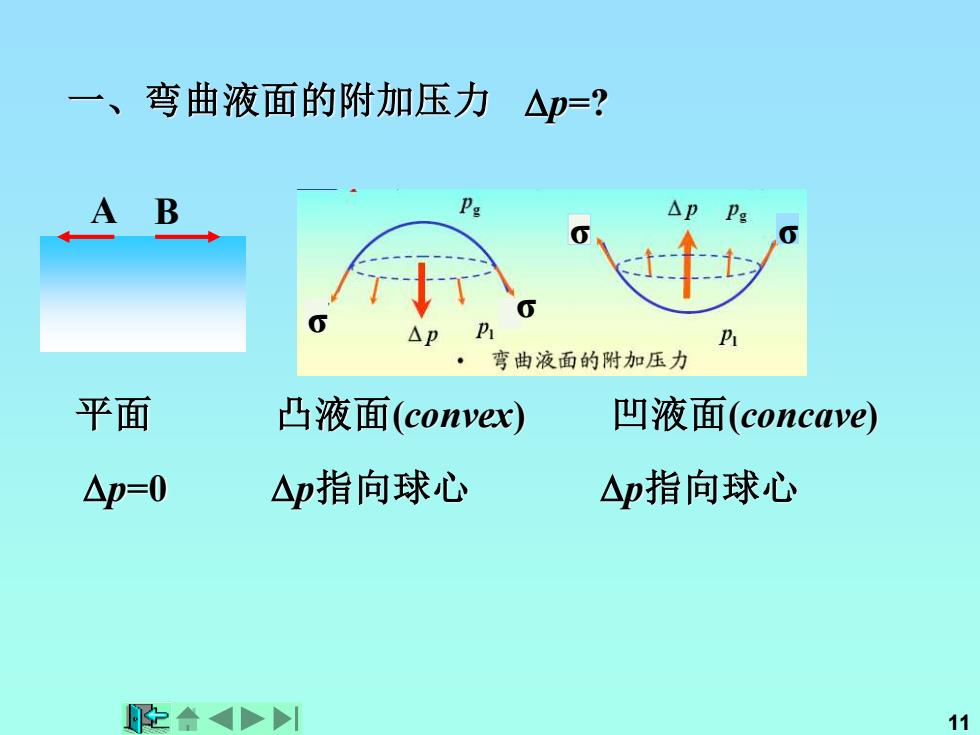
一、 弯曲液面的附加压力△p=? A B △pPg △p P 弯曲液面的附加压力 平面 凸液面(convex) 凹液面(concave) △p=0 △p指向球心 △p指向球心 E合4> 11
11 一、弯曲液面的附加压力 平面 凸液面(convex) 凹液面(concave) p=0 p指向球心 p指向球心 p=? A B σ σ σ σ

△p=? p'=p+p或△p=p'-p 实验: p'dv-pdy Apdv (p'-p)dv=odA dA d(4m2) △p=O -0 d d(4m3/3) 8nrdr 20 4à2 r 20 △p= Young-Laplace equation 陀合 12
12 p' = p +p或p=p'−p 实验: p dV pdV pdV ' − = ( p' −p)dV =dA(4 / 3) (4 ) 3 2 d r d r dV dA p = = r dr rdr 2 4 8 = r p 2 = Young-Laplace equation r 2 = 液体 p' p p=?

Young-Laplace公式:△p=2c/r 式中r:曲率半径。 越大,△p越小;平面时r→o,△p=0 注意: 1不管是凸液面,还是凹液面,附加压力的方向总是 指向球心,凸液面下的液体压力偏大pp+p), 凹液面下液体压力偏小pp-p); 2.对于液泡,如肥皂泡,泡内气体的压力比泡外压力 大,其差值为△p=4σ/r 合4D 13
13 Young-Laplace 公式 : p=2/r 式中r:曲率半径。 r越大,p越小;平面时r→,p =0 注意: 1.不管是凸液面,还是凹液面,附加压力的方向总是 指向球心,凸液面下的液体压力偏大(p凸=p+p) , 凹液面下液体压力偏小(p凹=p-p) ; 2. 对于液泡,如肥皂泡,泡内气体的压力比泡外压力 大,其差值为 p=4/r
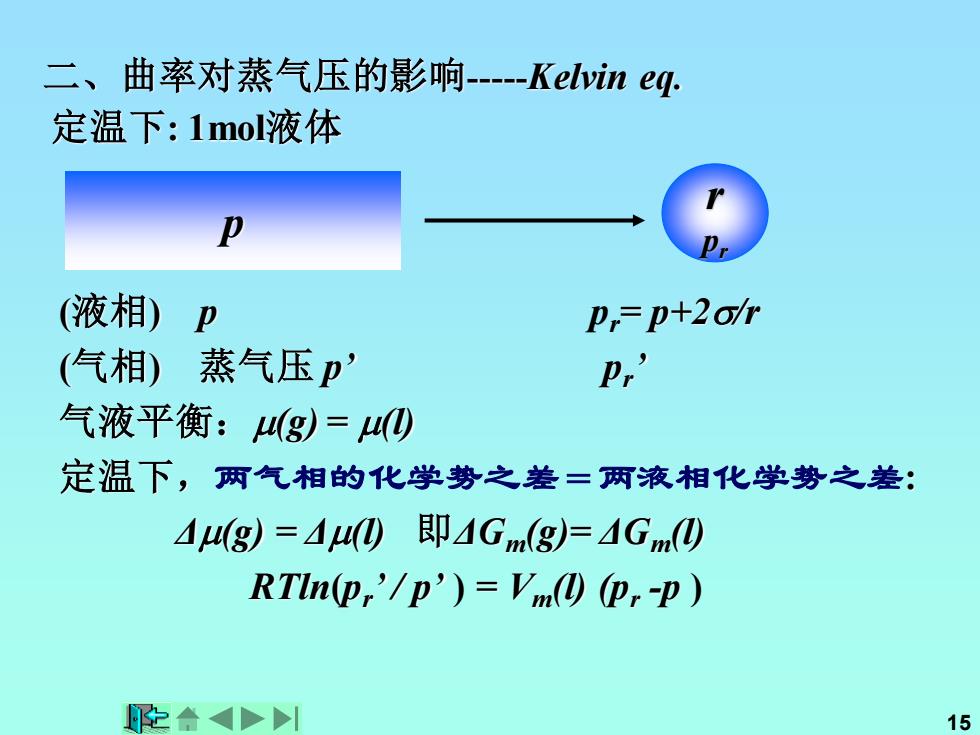
二、曲率对蒸气压的影响-Kelvin eq. 定温下:1mol液体 (液相)卫 P,=p+2o/r (气相)蒸气压p' P’ 气液平衡:4(g)=4(四 定温下,两气相的化学势之差=两液相化学势之差: 44(g=40即1Gmg=AGm) RTIn(p,'/p')=Vm((P,-P) 在合> 15
15 二、曲率对蒸气压的影响-Kelvin eq. 定温下: 1mol液体 (液相) p pr= p+2/r (气相) 蒸气压 p’ pr ’ 气液平衡:(g) = (l) 定温下,两气相的化学势之差=两液相化学势之差: Δ(g) = Δ(l) 即ΔGm(g)= ΔGm(l) RTln(pr ’ / p’ ) = Vm(l) (pr -p ) r pr p

Kelvin eq. p In Pr V()20 之 RTr 2Mo In p RTrp 注意: 凹 (液中气泡):取负值,p,p (小液滴):取正值,p,'>p 16
16 Kelvin eq. RTr V l p pr m ( )2 ln = RTr M p pr 2 ln = 注意: 凹(液中气泡):r取负值,pr ’< p’ 凸(小液滴): r取正值,pr ’> p’ r V l p p RT m r 2 ln = ( )