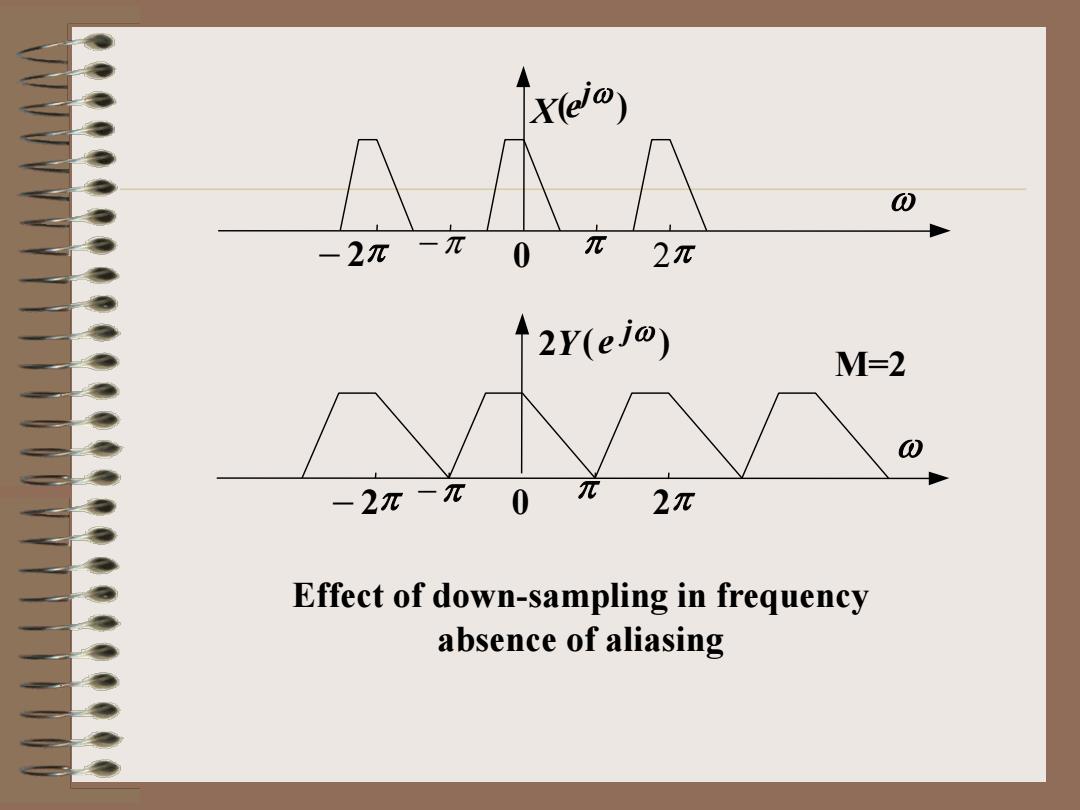
Ixe@) -2π-π0元2π ↑2Y(ejo) M=2 0 -2π-π 0元2π Effect of down-sampling in frequency absence of aliasing
Effect of down-sampling in frequency absence of aliasing ( ) jω X e ω 0 − 2π −π π 2π 2 ( ) jω Y e M=2 ω 0 π − 2π −π 2π
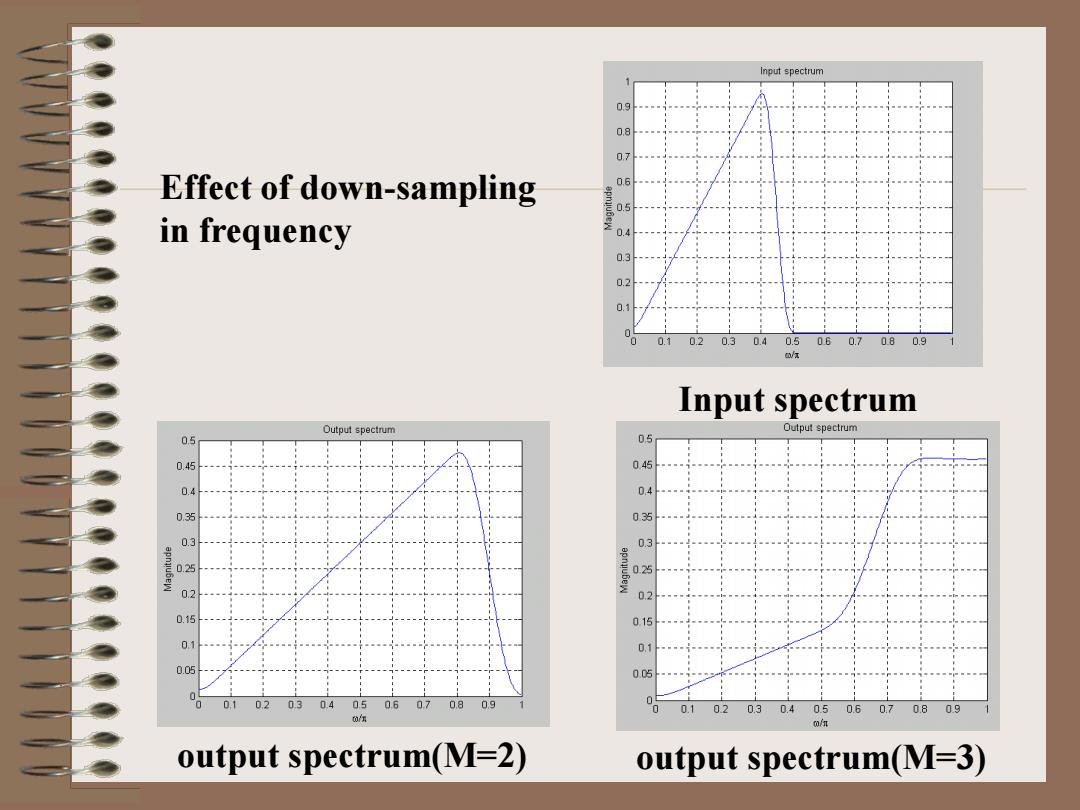
Input spectrum 09 0.8 07 Effect of down-sampling 0.6 05 in frequency 0.4 0.3 0.1 02 0.5 06 0.7 08 0.9 Input spectrum Output spectrum Output spectrum 05 045 04 035 03 0 02 02 0.15 015 01 01 0.05 0.05 0.10.2 0.30.405060708 09 01 02 03 0.4 050.6 0.7 0.8 09 0/ output spectrum(M-2) output spectrum(M=3)
Effect of down-sampling in frequency Input spectrum output spectrum(M=2) output spectrum(M=3)

S 10.2 Filters In Sampling Rate Alteration Cascade Equivalences Case 1 x(n] [n ◆2 y [n] x v2[n] y2可 IM For the left-hand side figure,we have V=X(z) M-1 y(2)=立∑X(zMW) k=0 For the right-hand side figure,we have M-1 M- V(a)=方∑X(zMW)Y,(z)=立∑X(zMW) k=0 k=0 Since L and M are relatively prime,Wyk and WKL take the same set of values for k=0,1,...,M-1. Hence Y(Z)=Y2(Z)
§10.2 Filters In Sampling Rate Alteration Cascade Equivalences Case 1 For the left-hand side figure,we have V1=X(zL) ( ) ( ) 1 0 1 / 1 ∑ − = = M k kL M L M Y z M X z W For the right-hand side figure,we have ( ) ( ) 1 0 1 1/ 2 ∑ − = = M k k M M V z M X z W ( ) ( ) 1 0 1 / 2 ∑ − = = M k k M L M Y z M X z W Since L and M are relatively prime, WM k and WM kL take the same set of values for k=0,1,…, M-1. Hence Y1(z)=Y2(z)