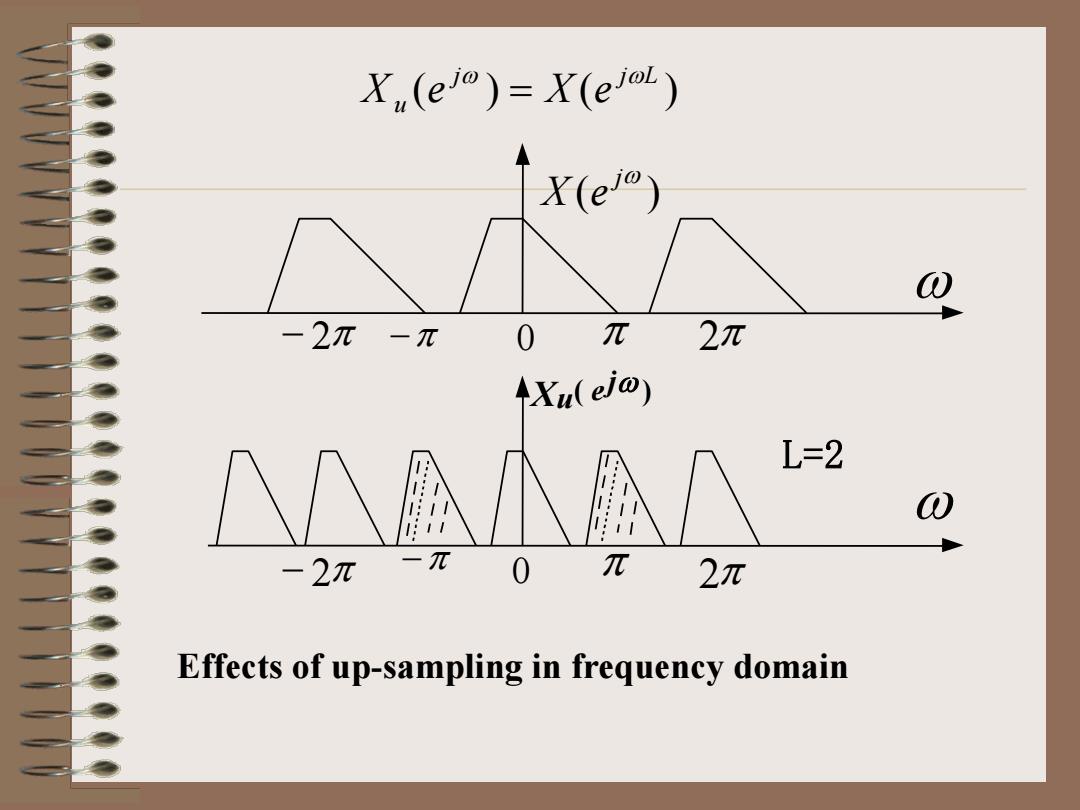
X(e)=X(ej) X(e) 0 -2π-元 0 π 2π AXu(ej@) L=2 -2π 0 π 2π Effects of up-sampling in frequency domain
( ) ( ) j j L u X e X e ω ω = Effects of up-sampling in frequency domain ( ) jω X e ω − 2π −π 0 π 2π ( ω ) j u X e L=2 ω 0 π 2π −π − 2π

Considering down-sampler Y(z)=∑x[Mm]z” n=-00 Let Then, 00 00 Y(e)=∑x[M例]z"=∑xn[Mim]z" n=-o0 00 = xt[k]z/M=Xn(zM) k=-00
Considering down-sampler = ∑ ∞ =−∞ − n n Y(z) x[Mn]z Let Then, = ∑ = ∑ ∞ =−∞ − ∞ =−∞ − n n n n Y(z) x[Mn]z x [Mn]z int [ ] ( ) 1/ int / int M k k M = ∑ x k z = X z ∞ =−∞ − x [ n ] = int x[n], n=0, ±M, ±2M,… 0, otherwise

Now Xint n]can be related to x[n] through xint[n]=x[n]c[n] [1,n=0,±M,+2M,… 0,otherwise A convenient representation is given by(Problem 10.4) 时2r M-1 k=0 where Wy =e-i2zIM
Now xint[n] can be related to x[n] through [ ] [ ] [ ] xint n = x n c n = ± ± = otherwise n M M c n 0, 1, 0, , 2 ,... [ ] A convenient representation is given by(Problem 10.4) 1 0 1 [ ] M kn M k cn W M − − = = ∑ where j M M W e− 2π / =
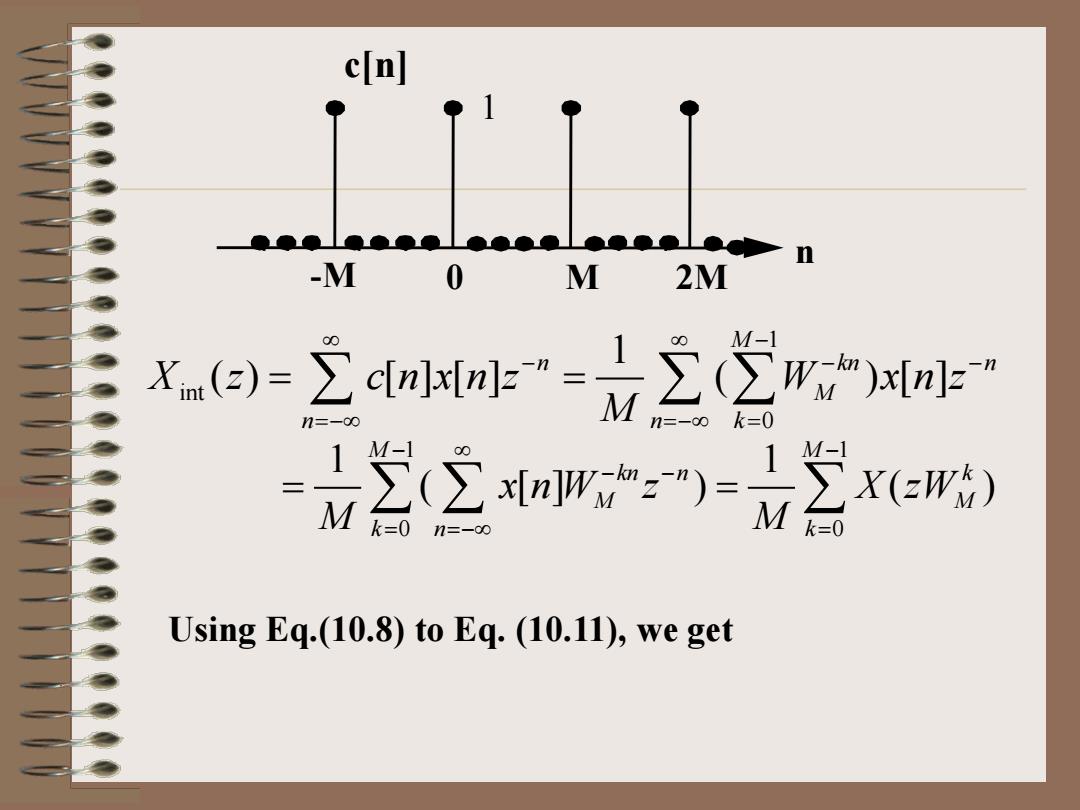
c n -M 0 M 2M X.e)立eaa啡立2m,a 00 M-1 n=-00 n=-o0k=0 22r*) M ∑X(zW) k=0 n=-00 =0 Using Eq.(10.8)to Eq.(10.11),we get
1 int 0 1 () [ ][ ] ( )[ ] M n kn n M n n k X z cnxnz W xnz M ∞ ∞ − − − − =−∞ =−∞ = = ∑ ∑∑ = 1 1 0 0 1 1 ( [] ) ( ) M M kn n k M M k n k x n W z X zW M M − ∞ − − − = =−∞ = = ∑∑ ∑ = Using Eq.(10.8) to Eq. (10.11), we get -M 0 M 2M 1 c[n] n
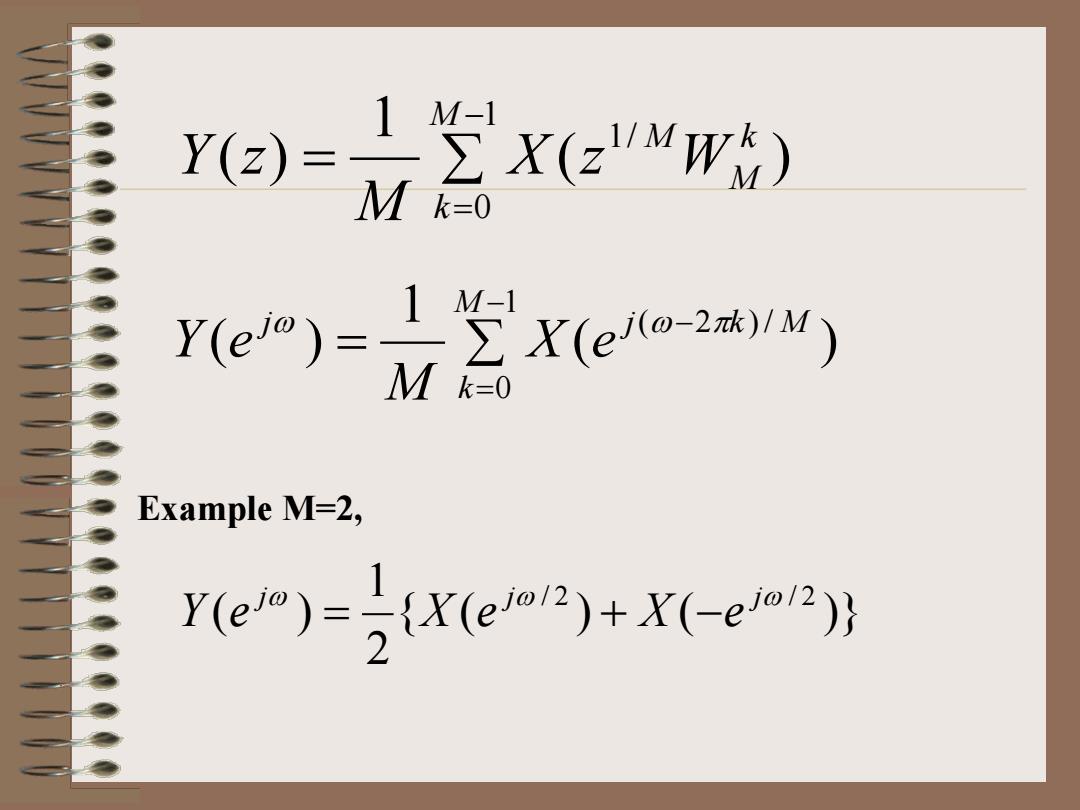
1 M-1 Y(z)=∑X(zMW) M=0 e)点ewsM Example M=2, e)-Ke)+x-emy
= ∑ − = 1 0 1/ ( ) 1 ( ) M k k M M X z W M Y z = ∑ − = − 1 0 ( 2 )/ ( ) 1 ( ) M k j j k M X e M Y e ω ω π Example M=2, { ( ) ( )} 2 1 ( ) jω jω / 2 jω / 2 Y e = X e + X −e