
欧拉七桥问题 后来大数学家欧拉把它转化成一个几何问题一一笔画问题。他不仅解决了此问 题,且给出了连通图可以一笔画的充要条件是:奇点的数目不是0个就是2个 (连到一点的数目如是奇数条,就称为奇点,如果是偶数条就称为偶点,要想一 笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两 端,因此任何图能一笔画成,奇点要么没有要么在两端)。因此,7桥问题无解
欧拉七桥问题 6 后来大数学家欧拉把它转化成一个几何问题——一笔画问题。他不仅解决了此问 题,且给出了连通图可以一笔画的充要条件是:奇点的数目不是0 个就是2 个 (连到一点的数目如是奇数条,就称为奇点,如果是偶数条就称为偶点,要想一 笔画成,必须中间点均是偶点,也就是有来路必有另一条去路,奇点只可能在两 端,因此任何图能一笔画成,奇点要么没有要么在两端)。因此,7桥问题无解
3.2基本概念 ·图:指由若干节点及连接这些点的线组成的图形。 。节点:表示某一具体事物 。边或弧:表示事物之间某种特定关系。 ·连通图:任何两点之间可由一条或多条边相连。否则就是不连通的。 ·圈:若图中某一点边顺序衔接序列中,始点和终点重合,则称之为圈。 。1 例如:A-B-E-C-A A-B-E-F-D-A B E A D
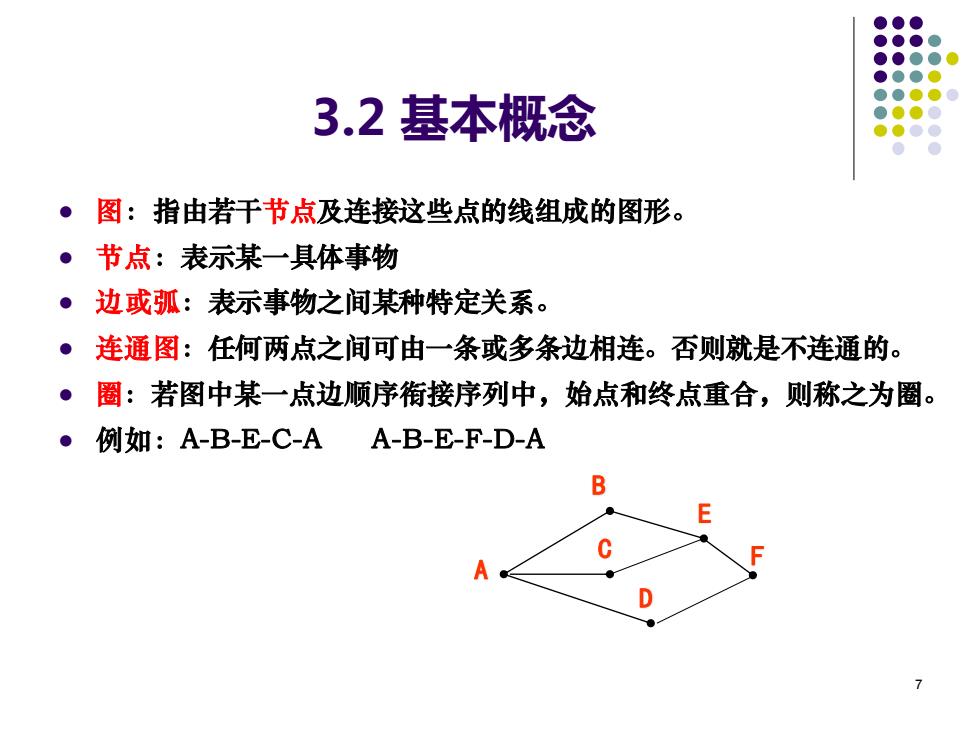
7 3.2 基本概念 ⚫ 图:指由若干节点及连接这些点的线组成的图形。 ⚫ 节点:表示某一具体事物 ⚫ 边或弧:表示事物之间某种特定关系。 ⚫ 连通图:任何两点之间可由一条或多条边相连。否则就是不连通的。 ⚫ 圈:若图中某一点边顺序衔接序列中,始点和终点重合,则称之为圈。 ⚫ 例如:A-B-E-C-A A-B-E-F-D-A B A C D E F
3.2基本概念 树:即是一个无圈的连通图。 事故树:从结果到原因描绘事故发生的有向逻辑树。树中的节点具 有逻辑判断性质。 B E 图构成树的两个限制条件 有向性:要求连接线的方向根据输入和输出来规定 开放性:要求必须保证不形成回路
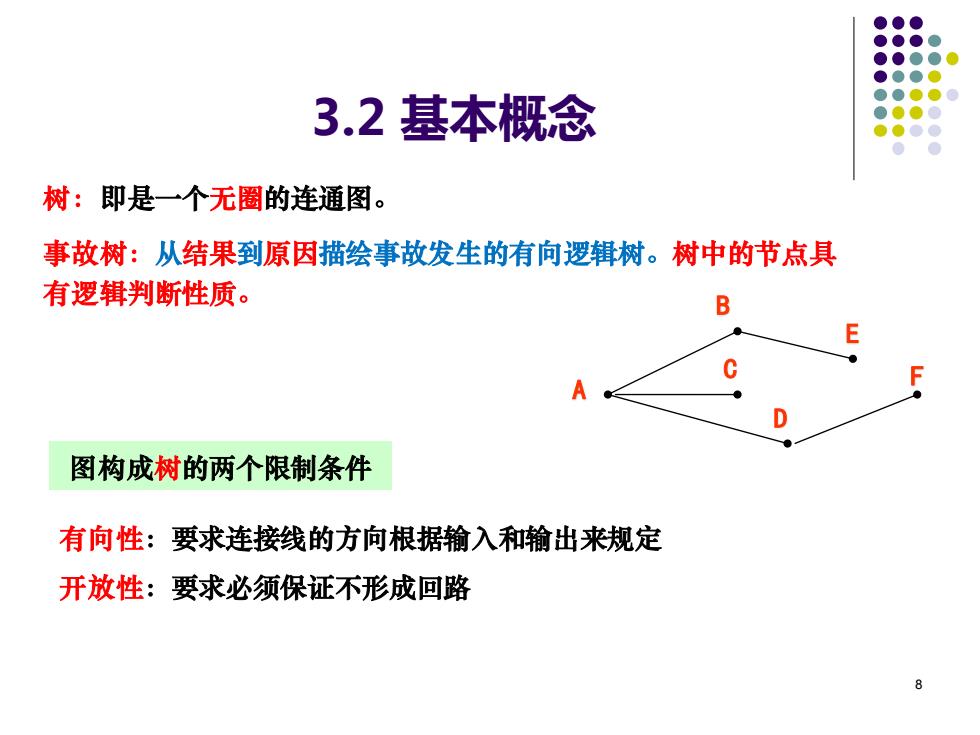
8 3.2 基本概念 树:即是一个无圈的连通图。 事故树:从结果到原因描绘事故发生的有向逻辑树。树中的节点具 有逻辑判断性质。 B A C D E F 图构成树的两个限制条件 有向性:要求连接线的方向根据输入和输出来规定 开放性:要求必须保证不形成回路

事故树的概念 ·形似倒立着的树。 ●树的“根部”顶点节点表示系统的某一个事故, ●树的“梢”底部节点表示事故发生的基本原因, ●树的“枝权”中间节点表示由基本原因促成的事故结果,又是系统事 故的中间原因; ●事故因果关系的不同性质用不同的逻辑门表示。 这样画成的一个“树”用来描述某种事故发生的因果关系,称之为事 故树
9 事故树的概念 ⚫ 形似倒立着的树。 ⚫ 树的“根部”顶点节点表示系统的某一个事故, ⚫ 树的“梢”底部节点表示事故发生的基本原因, ⚫ 树的“枝杈”中间节点表示由基本原因促成的事故结果,又是系统事 故的中间原因; ⚫ 事故因果关系的不同性质用不同的逻辑门表示。 ⚫ 这样画成的一个“树”用来描述某种事故发生的因果关系,称之为事 故树

3.3事故树分析方法的步骤 ·事故树分析是根据系统可能发生的事故或已经发生的事故所提供的信 息,去寻找同类事故发生有关的原因,从而采取有效的防范措施,防 止同类事故再次发生。 ·事故树分析的主要步骤包括: 。3.3.1编制事故树 ·3.3.2事故树定性分析 ·3.3.3事故树定量分析 ●3.3.4制定预防事故和改进系统的措施 10
10 3.3 事故树分析方法的步骤 ⚫ 事故树分析是根据系统可能发生的事故或已经发生的事故所提供的信 息,去寻找同类事故发生有关的原因,从而采取有效的防范措施,防 止同类事故再次发生。 ⚫ 事故树分析的主要步骤包括: ⚫ 3.3.1 编制事故树 ⚫ 3.3.2 事故树定性分析 ⚫ 3.3.3 事故树定量分析 ⚫ 3.3.4 制定预防事故和改进系统的措施