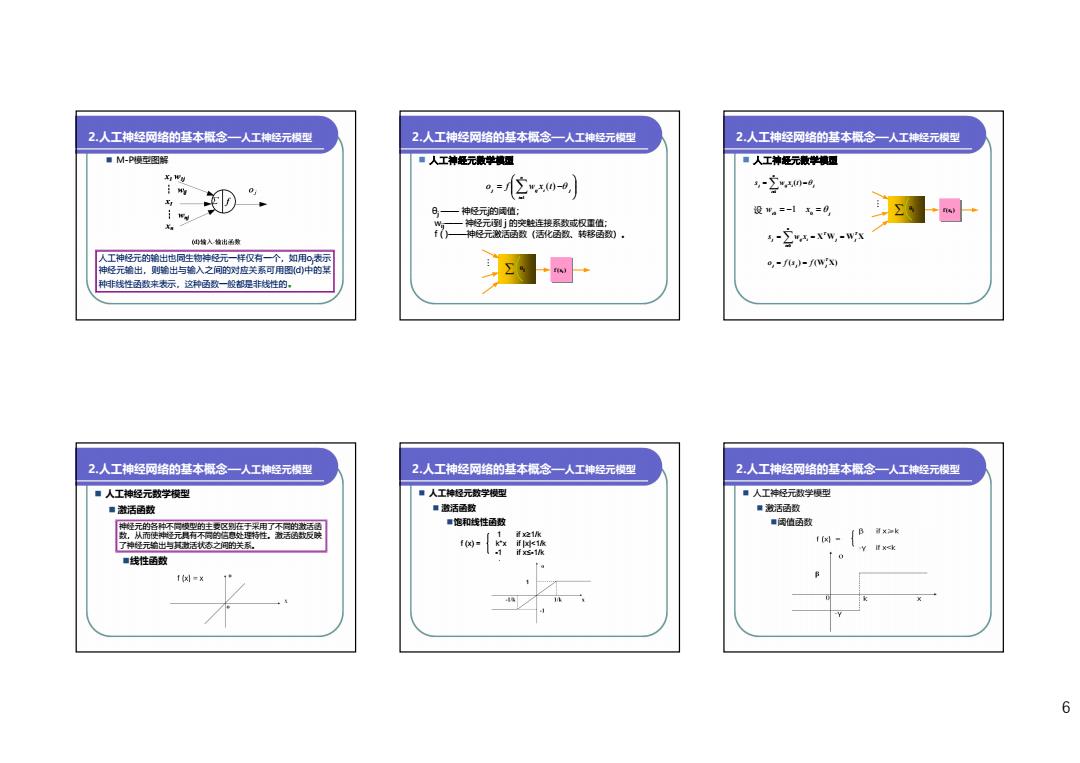
2.人工神经网络的基本叔念一人工神经元模型 2,人工神经网络的基本概念一人工神经元模型 2,人工神经网络的基本概念一人工神经元模型 ■M-P模图解 ■人工神是元败学模通 ■人工神经元散学模豆 XIW ” 。=它x- 20-g 神经元的话值: 设w。=-1无=0 ,经元到j的突触连接系数或权重值: 四 神经元激活通数(活化函数、转移陋), 与w 人工神经元的增出也同生物芹经元一样取有一个,如用©表示 0,-f6,)-fwx) 神经元输出,则输出与输入之问间的对应关系可用图(d中的某 种非线性函数来枣示。这种函数一般都是非线性的。 四 2.人工神经网络的基本概念、一人工神经元模型 2.人工神经网络的基本概念一人工排经元模型 2.人工神经网络的基本概念一人工神经元模型 ■人工神经元数学模型 ■人工神经元数学模型 ■人工持经元数学模型 ■激活函数 ■泼活涵数 ■就活函数 神经元的各种不同陵型的主蒙区在于采用了不的话利 ■饱和线性函数 ■闭值函数 数,从而使种经元其有不同店息处理特在,话数反碳 ix21/k 了神经元给出与活状态之间的关系。 if x5-1/k V量<水 ■线性函敬 1= 6
6 2.人工神经网络的基本概念—人工神经元模型 M-P模型图解 人工神经元的输出也同生物神经元一样仅有一个,如用oj表示 神经元输出,则输出与输入之间的对应关系可用图(d)中的某 种非线性函数来表示,这种函数一般都是非线性的。 2.人工神经网络的基本概念—人工神经元模型 人工神经元数学模型 n i j ij i j o f w x t 1 ( ) θj —— 神经元j的阈值; wij—— 神经元i到 j 的突触连接系数或权重值; f ( )——神经元激活函数(活化函数、转移函数)。 M ( )i j f s 2.人工神经网络的基本概念—人工神经元模型 人工神经元数学模型 n i j ij i j s w x t 1 ( ) ( ) (W X) T j j j o f s f 设 wi0 1 j x0 X W W X T j j T n i j ij i s w x 0 M j f (si) 2.人工神经网络的基本概念—人工神经元模型 人工神经元数学模型 激活函数 线性函数 神经元的各种不同模型的主要区别在于采用了不同的激活函 数,从而使神经元具有不同的信息处理特性。激活函数反映 了神经元输出与其激活状态之间的关系。 2.人工神经网络的基本概念—人工神经元模型 人工神经元数学模型 激活函数 饱和线性函数 1 if x≥1/k f (x) = k*x if |x|<1/k -1 if x≤-1/k 2.人工神经网络的基本概念—人工神经元模型 人工神经元数学模型 激活函数 阈值函数
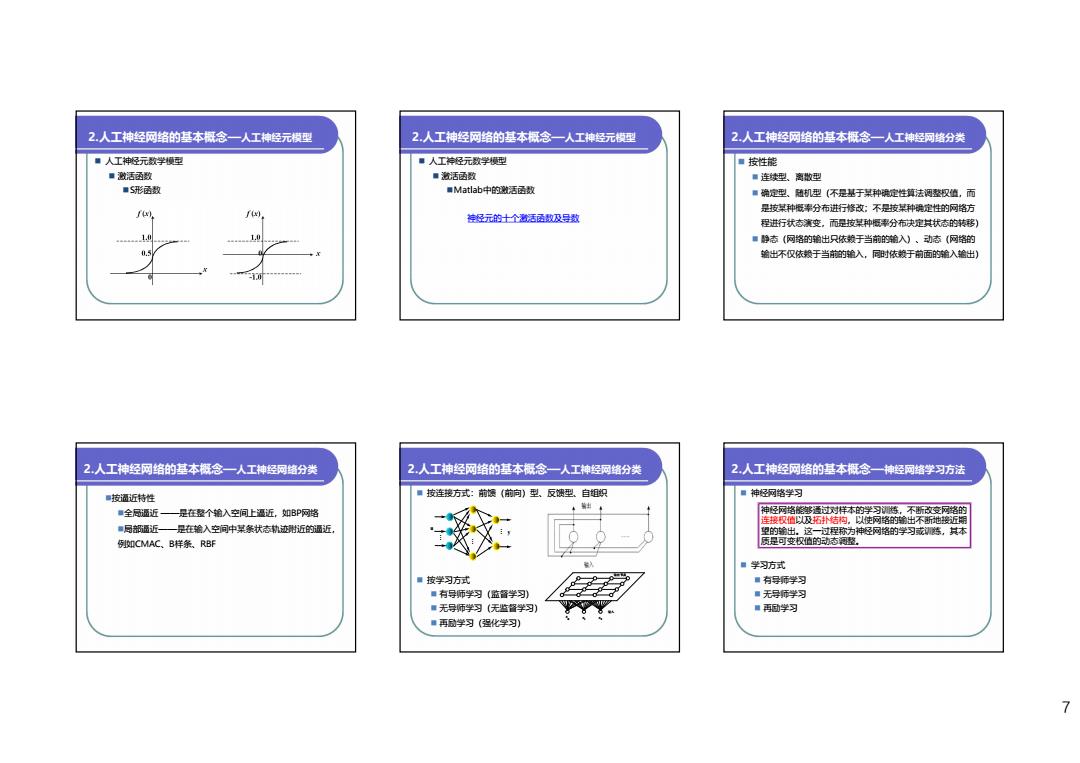
2.人工神经网络的基本叔念一人工神经元模型 2,人工神经网络的基本概念一人工神经元模型 2人工神经网络的基本概念一人工神经网络分类 ■人工神经元数学横型 ■人工持经元数学横型 ■按性能 ■融活函数 ■意活函数 ■连续型、离散型 ■S形函数 ■Matlab中的嫩活函数 ■确定型、随机型(不是基于某种定性算法调整权值,而 f 是按某种概率分布进行修改:不是按某种确定性的网路方 #经元的士个着活语数及导数 程进行状态演变,而是按某种概分布决定其状态的转移) ■静态(网路的输出只依数于当前的输入)、动态(网路的 输出不仅依赖于当前的维入,同时依赖于前面的端入缩出) 2,人工神经网络的基本概念一人工神经网络分类 2,人工神经网络的基本标念一人工神经网络分类 2,人工神经网络的基本概念一神经网络学习方法 ●按酒近特性 ■按连接方式:前烦(前向)型、反馈型.自组织 ■神经网络学习 ■全通近—是在整个输入空问上逼近,如BP网路 神经网路部适过对样本的学习测陈,不断改交网路的 连接权值以及拓扑结构。以使网路的罐出不断地接近期 ■局部画近一是在输入空问中某条状态轨迹附近的通近, 望的罐出。这一过程称为神经网格的学习或慈,其本 例如CMAC、B样条、RBF 质是可变权值的动态整 ■学习方式 ■按学习方式 ■有导师学习 ■有导师学习(监督学习) ■无寻师学习 ■无号师学习(无监督学习) ■再团学习 ■再励学习(程化学习) 7
7 2.人工神经网络的基本概念—人工神经元模型 人工神经元数学模型 激活函数 S形函数 2.人工神经网络的基本概念—人工神经元模型 人工神经元数学模型 激活函数 Matlab中的激活函数 神经元的十个激活函数及导数 2.人工神经网络的基本概念—人工神经网络分类 按性能 连续型、离散型 确定型、随机型(不是基于某种确定性算法调整权值,而 是按某种概率分布进行修改;不是按某种确定性的网络方 程进行状态演变,而是按某种概率分布决定其状态的转移) 静态(网络的输出只依赖于当前的输入)、动态(网络的 输出不仅依赖于当前的输入,同时依赖于前面的输入输出) 2.人工神经网络的基本概念—人工神经网络分类 按逼近特性 全局逼近 ——是在整个输入空间上逼近,如BP网络 局部逼近——是在输入空间中某条状态轨迹附近的逼近, 例如CMAC、B样条、RBF 2.人工神经网络的基本概念—人工神经网络分类 按连接方式:前馈(前向)型、反馈型、自组织 按学习方式 有导师学习(监督学习) 无导师学习(无监督学习) 再励学习(强化学习) M M M u y 输出节点 输入 0 x 1x 2 x 2.人工神经网络的基本概念—神经网络学习方法 神经网络学习 学习方式 有导师学习 无导师学习 再励学习 神经网络能够通过对样本的学习训练,不断改变网络的 连接权值以及拓扑结构,以使网络的输出不断地接近期 望的输出。这一过程称为神经网络的学习或训练,其本 质是可变权值的动态调整
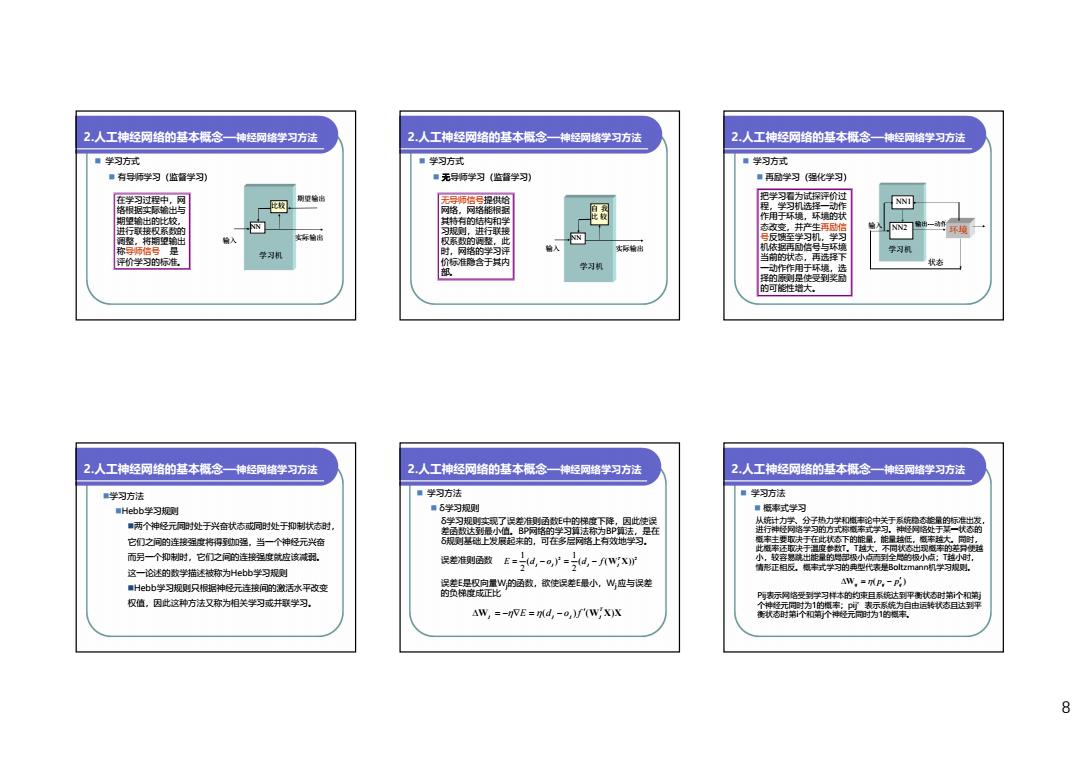
2,人工神经网络的基本概念一神经网络学习方法 2.人工神经网络的基本概念一神经网络学习方法 2人工神经网络的基本概念一神经网络学习方法 ■学习方式 ■学习方式 ■学习方式 ■有导师学习(监督学习)】 ■无导师学习(监督学习) ■再品学习程化学习) 在学习过程中,网 无导师信号提供 把学习石为试探评价过 据中输出与 网路。网络能报廷 程,学习机选择 动作 期里输出的比 其特有的结构和学 周 作用于环境,环境的状 进行联接权系的 N 习规则进行联接 态改变,并产生再励信 环境 仅系数的调整 称导师信号是 入 实诉输出 评价学习的标准 学习机 学习机 价准含于其内 当前的状态,再选轻下 学习机 动作作用于环境, 状态 择的原测是使受到奖励 的可能性增大, 2,人工神经网络的基本概念一神经罚络学习方法 2.人工神经网络的基本餐念一神经网络学习方法 2.人工神经网络的基本概念一神经网络学习方法 学习方法 ■学习方法 ■学习方法 ■Hebb学习规则 ■5学习规则 ■概率式学习 ■两个神经元可时处于兴奋状态或同时处于抑制状杏时」 6学习规实现了误差则函数E中的样度下降,因此使保 从统针力学、分子热力学和瓶丰论中关于系统隐态整量的标准出发 差数达到最小值,BP网路的学习法称为BP法,是在 进行神经同路学习的方式称草率式学习。种经码处于某一状态的 它们之间的连接强度将得到功加温。当一个神经元兴奋 规则础上发展起来的,可在多层网路上有效地学习. 登率主费取决于在此状态下的能量。能量越低,图率越大,司时, 而另一个抑制时,它们之问的连接程度就应该减现. 误差准则数E=片d,-o,护=d,-fwxr 这一论述的数学描述被称为Hebb学习规测 情形征相反,概中式学习的典型代表是Boltzmann机学习规则. ■Hebb学习规则只根据神经元连接问的激活水平改变 误差E是权向量W的函数,欲使误差最小,W应与误差 AW.=mP,-P) 的负梯成成证比 P阿支示网馅受到学习样本的约束且系构达到平衡状态时第个和第 权值,因此这种方法又称为相关学习或并联学习, AW,=-nvE=nd,-o,)f(W'X)X 8
8 2.人工神经网络的基本概念—神经网络学习方法 学习方式 有导师学习(监督学习) 在学习过程中,网 络根据实际输出与 期望输出的比较, 进行联接权系数的 调整,将期望输出 称导师信号 是 评价学习的标准。 期望输出 实际输出 学习机 输入 NN 比较 2.人工神经网络的基本概念—神经网络学习方法 学习方式 无导师学习(监督学习) 无导师信号提供给 网络,网络能根据 其特有的结构和学 习规则,进行联接 权系数的调整,此 时,网络的学习评 价标准隐含于其内 部。 实际输出 学习机 输入 NN 自 我 比 较 2.人工神经网络的基本概念—神经网络学习方法 学习方式 再励学习(强化学习) 把学习看为试探评价过 程,学习机选择一动作 作用于环境,环境的状 态改变,并产生再励信 号反馈至学习机,学习 机依据再励信号与环境 当前的状态,再选择下 一动作作用于环境,选 择的原则是使受到奖励 的可能性增大。 状态 输入 NN1 NN2 学习机 输出---动作 环境 2.人工神经网络的基本概念—神经网络学习方法 学习方法 Hebb学习规则 两个神经元同时处于兴奋状态或同时处于抑制状态时, 它们之间的连接强度将得到加强,当一个神经元兴奋 而另一个抑制时,它们之间的连接强度就应该减弱。 这一论述的数学描述被称为Hebb学习规则 Hebb学习规则只根据神经元连接间的激活水平改变 权值,因此这种方法又称为相关学习或并联学习。 2.人工神经网络的基本概念—神经网络学习方法 学习方法 δ学习规则 δ学习规则实现了误差准则函数E中的梯度下降,因此使误 差函数达到最小值。BP网络的学习算法称为BP算法,是在 δ规则基础上发展起来的,可在多层网络上有效地学习。 误差准则函数 2 2 ( ( )) 2 1 ( ) 2 1 W X T j j j j E d o d f 误差E是权向量Wj的函数,欲使误差E最小,Wj 应与误差 的负梯度成正比 W ( ) (W X)X T j j j j E d o f 2.人工神经网络的基本概念—神经网络学习方法 学习方法 概率式学习 从统计力学、分子热力学和概率论中关于系统稳态能量的标准出发, 进行神经网络学习的方式称概率式学习。神经网络处于某一状态的 概率主要取决于在此状态下的能量,能量越低,概率越大。同时, 此概率还取决于温度参数T。T越大,不同状态出现概率的差异便越 小,较容易跳出能量的局部极小点而到全局的极小点;T越小时, 情形正相反。概率式学习的典型代表是Boltzmann机学习规则。 Pij表示网络受到学习样本的约束且系统达到平衡状态时第i个和第j 个神经元同时为1的概率;pij’表示系统为自由运转状态且达到平 衡状态时第i个和第j个神经元同时为1的概率。 ( ) ij pij pij W
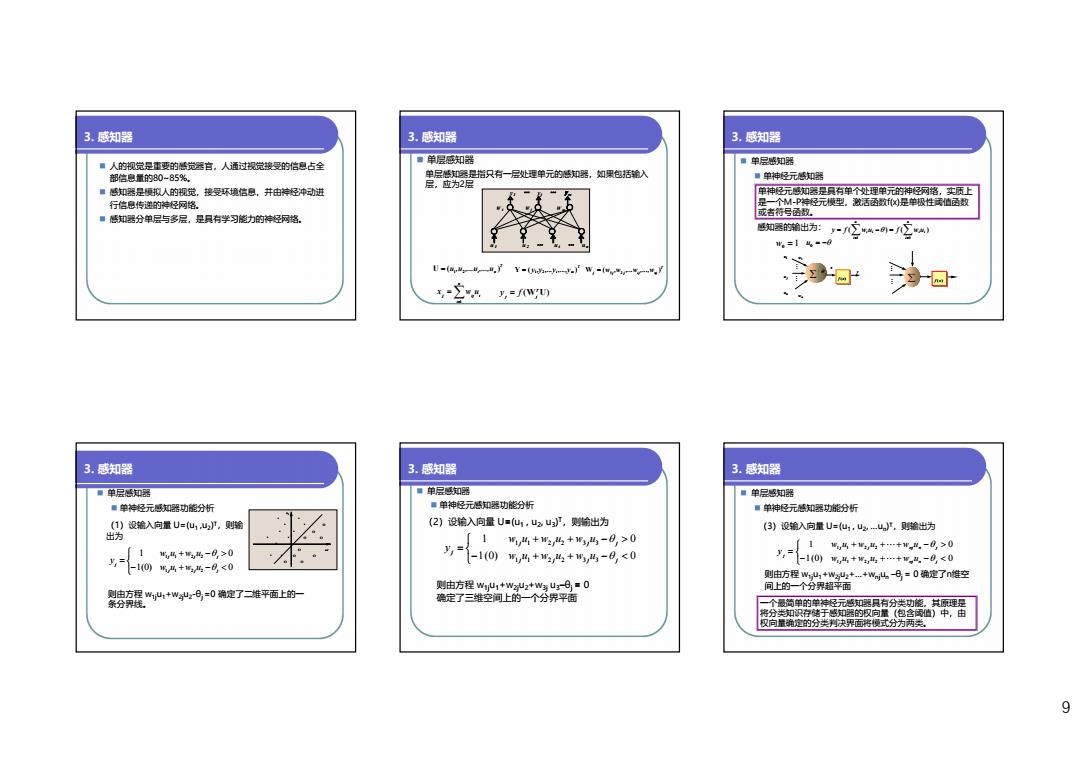
3.感知器 3.感知器 3.感知器 ■人的视觉是重要的感觉远官,人通过视觉接受的信恩占全 ■单层感知器 ■单层感知器 部信息量的80-85%, 单层感知堡是指只有一层处理单元的感知器,如果包括输入 ■单神经元感知器 ■感知器是模拟人的视觉。接受环境信息,并由梓经冲动进 层.应为2层 单神元感如深是具有单个处理单元的神经网络,实质上 行信吧传递的裤经网路. 是一个M-P裤经元模型。激活函数)是单极性无值函数 或者衍号函数。 ■感知器分单层与多层,是具有学习能力的裤经网路。 感如器的端出为:-立--A) w。=14=-0 0-4-,了Y-h-W,-w一- -24,=w四 酒分 @ 3.感知器 3.感知器 3.感知器 ■单层感知器 ■单层感知器 ■单层感知器 ■单裤经元感知器功能分析 ■单神经元感知器功能分析 ■单神经元感知器功能分析 (1)设输入向量U=(u1u)开,则输 (2)设输入向量U=仙1,2u,则输出为 (3)设输入向量U=(仙,u-山,,则输出力 出为 154+w西+53,4-0,>0 【1 ,= ,马+,十+…+w。-0,>0 y,= 马+5码-8>0 -1(0),4+2%+,%-8,<0 y,={-10"品+w品++g,L-0<0 1064+4-8<0 则由方程w,+w2++w儿-号=0确定了n雄空 则由方程w1心1+w2+WU日■0 间上的一个分界超平面 则由方程W1山1+w2-8=0确定了二维平面上的一 条分界线. 确定了三维空间上的一个分界平面 一个额简单的单裤经元感知器只有分类功能。其原理是 将分类知识行储于感加熙的权向量(包含阀值)中,由 权向量确定的分类判决界面粥模式分为两类, 9
9 3. 感知器 人的视觉是重要的感觉器官,人通过视觉接受的信息占全 部信息量的80~85%。 感知器是模拟人的视觉,接受环境信息,并由神经冲动进 行信息传递的神经网络。 感知器分单层与多层,是具有学习能力的神经网络。 3. 感知器 单层感知器 单层感知器是指只有一层处理单元的感知器,如果包括输入 层,应为2层 y1 … yj … y m W 1 ○ W j ○ W m○ ○ ○ ○ ○ u1 u2 … ui … un T i n (u ,u ,...u ,...,u ) U 1 2 T i m ( y ,y ,...y ,...,y ) Y 1 2 T j j j ij nj (w ,w ,...w ,...,w ) W 1 2 n i j ij i x w u 1 (W U) T j j y f 3. 感知器 单层感知器 单神经元感知器 单神经元感知器是具有单个处理单元的神经网络,实质上 是一个M-P神经元模型,激活函数f(x)是单极性阈值函数 或者符号函数。 感知器的输出为: ( ) ( ) 1 0 n i i i n i y f wiui f w u w0 1 u0 n j u u u1 M M y x wn w1 f (x) M M f (x) 3. 感知器 单层感知器 单神经元感知器功能分析 1(0) 0 1 0 1 1 2 2 1 1 2 2 j j j j j j j w u w u w u w u y (1)设输入向量 U=(u1 ,u2 )T,则输 出为 则由方程 w1ju1+w2ju2 -θj =0 确定了二维平面上的一 条分界线。 u1 * * * * O * * O * * O O * O u2 * * O O O O 3. 感知器 单层感知器 单神经元感知器功能分析 1(0) 0 1 0 1 1 2 2 3 3 1 1 2 2 3 3 j j j j j j j j j w u w u w u w u w u w u y (2)设输入向量 U=(u1 , u2 , u3 )T,则输出为 则由方程 w1ju1+w2ju2+w3j u3 –θj = 0 确定了三维空间上的一个分界平面 3. 感知器 单层感知器 单神经元感知器功能分析 1(0) 0 1 0 1 1 2 2 1 1 2 2 j j nj n j j j nj n j j w u w u w u w u w u w u y (3)设输入向量 U=(u1 , u2 , …un )T,则输出为 则由方程 w1ju1+w2ju2+…+wnjun –θj = 0 确定了n维空 间上的一个分界超平面 一个最简单的单神经元感知器具有分类功能,其原理是 将分类知识存储于感知器的权向量(包含阈值)中,由 权向量确定的分类判决界面将模式分为两类

3.感知器 3.感知器 3.感知器 ■单的学习算波 ■单神经元感知器 ■线性可分集合 ■用于两类模式分类时相当于在高雄样本空同中,用一个超 ()二输平面上的两典模式,见表, 00 2☑输入样本对UPd,其中UP=-1,uRuP,一4,,d为则的 平面将两类样本分开. 用因所示二轴入苹轴出单是墙加悬, 0 轮出问量(导信号),上标印代表样本对的棱式京号,设样集 轴入着出超述: 0 中样本总数为L则p=1,2L ■已证明若罐入的两类模式是线性可分集合(指存在一个超 )计算各节点的实东给出 平面能将其分开),则法一定收数 y-f八0的+w:妇--f八) ∫1,20 11 10,c0 9等3 ■局限性:若输入梗式为线姓不可分集合。感知腰的学习算 法不收,不能进行正确分类 练的稳定姓,太小则使链的收敛速度变樱。一般取0<门s1: 0,w,41+w:3<0 可见:轴入输出为物性可分果合,一定可 找到一条直填,将轴入模式分为两漠 物建速知与速知●单习算法 3.感知器 3.感知器 3.感知器 ■线性可分集合 ■线性可分集合 ■线性可分集合 此直纳方在: (2)三维空间上的两类模式,见表, (2)三维空间上的两类模式,见表 F=4+w5-8-0 0 用所示三地入单始由的单脚港,轴入轴由, 平面仿餐: -吗+"4+w4---,20 y=+w马3+w,叫-0=0 见图,此直线与权值及腾值有关 0,·0 1,4+n4+w128 甲-6,4+%w<8 此平面权值是同植有关见图。 可具,输入着出为州性可分角合。一度可找一个平国。 可仲到>3地空间上的 将地入黑式沿为两典 的零面上内安顿大#养国 分为两洗,由n输入/单编 6地 甲面上两天铜公好我 出的单知器实现 10
10 3. 感知器 单层感知器的学习算法 构建感知器与感知器学习算法 (1) 对各权值w0j(0),w1j(0),┄,wnj(0),j=1, 2,┄,m (m为计算层的 节点数)赋予较小的非零随机数; (2) 输入样本对{Up,dp},其中Up=(-1, u1p, u2p,┄,unp),dp为期望的 输出向量(导师信号),上标p代表样本对的模式序号,设样本集 中的样本总数为L,则 p=1, 2,┄,L; (3) 计算各节点的实际输出 (4) 调整各节点对应的权值,Wj(t+1)= Wj(t )+η[djp-yjp(t )]Up, j=1, 2,┄,m, 其中η为学习率,用于控制调整速度,太大会影响训 练的稳定性,太小则使训练的收敛速度变慢,一般取0<η≤1; (5) 返回到步骤(2)输入下一对样本,周而复始直到对所有样本, 感知器的实际输出与期望输出相等。 3. 感知器 单神经元感知器 用于两类模式分类时相当于在高维样本空间中,用一个超 平面将两类样本分开。 已证明若输入的两类模式是线性可分集合(指存在一个超 平面能将其分开),则算法一定收敛。 局限性:若输入模式为线性不可分集合,感知器的学习算 法不收敛,不能进行正确分类 3. 感知器 线性可分集合 (1) 二维平面上的两类模式,见表。 用图所示二输入/单输出单层感知器, 输入输出描述: 0 , 0 1 , 0 ( ) ( ) 1 1 2 2 y f w u w u f 即 1 1 2 2 1 1 2 2 0 , 1 , w u w u w u w u y 可见:输入输出为线性可分集合,一定可 找到一条直线,将输入模式分为两类 u u 1 2 y 0 0 0 1 0 0 0 1 0 1 1 1 3. 感知器 线性可分集合 此直线方程: y w u w u 1 1 2 2 0 则 u w w w 2 u 2 1 2 1 见图,此直线与权值及阈值有关。 u u 1 2 y 0 0 0 1 0 0 0 1 0 1 1 1 (a) 分类器结构 w2 w1 w0 y u0 1 2 1 u u u1 u2 (b) 平面上两类模式分界线 图 2-3-2 平面上两类模式分类 3. 感知器 线性可分集合 (2) 三维空间上的两类模式,见表。 用图所示三输入/单输出的单层感知器,输入输出: 0 , 0 1 , 0 ( ) ( ) 1 1 2 2 3 3 y f w u w u w u f 即 1 1 2 2 3 3 1 1 2 2 3 3 0 , 1 , w u w u w u w u w u w u y 可见,输入输出为线性可分集合,一定可找到一个平面, 将输入模式分为两类 u1 u2 u3 y 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 3. 感知器 线性可分集合 平面方程: y w1u1 w2u2 w3u3 0 则 2 3 2 1 3 1 3 3 u w w u w w w u 此平面与权值及阈值有关,见图。 (2) 三维空间上的两类模式,见表。 可引伸到n>3维空间上的 线性可分集合,一定可找 到一超平面,将输入模式 分为两类。由n输入/单输 出的单层感知器实现。 1 2 3 u u u y 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 w0 1 u0 y w1 w3 w2 3 2 1 u u u 2 u 1 u