Markov Chain for k-SAT Glauber Dynamics (X]VX2VX3)A(VXV x5)A (x4 Vx5VX6) Start from an arbitrary satisfyingx[T,F)V At each step: ·pick i∈V uniformly at random resample&~以~|ri) A:uniform distribution over all SAT solutionsx[T,F]V .(marginal distribution ofcond.on current values of all other variables
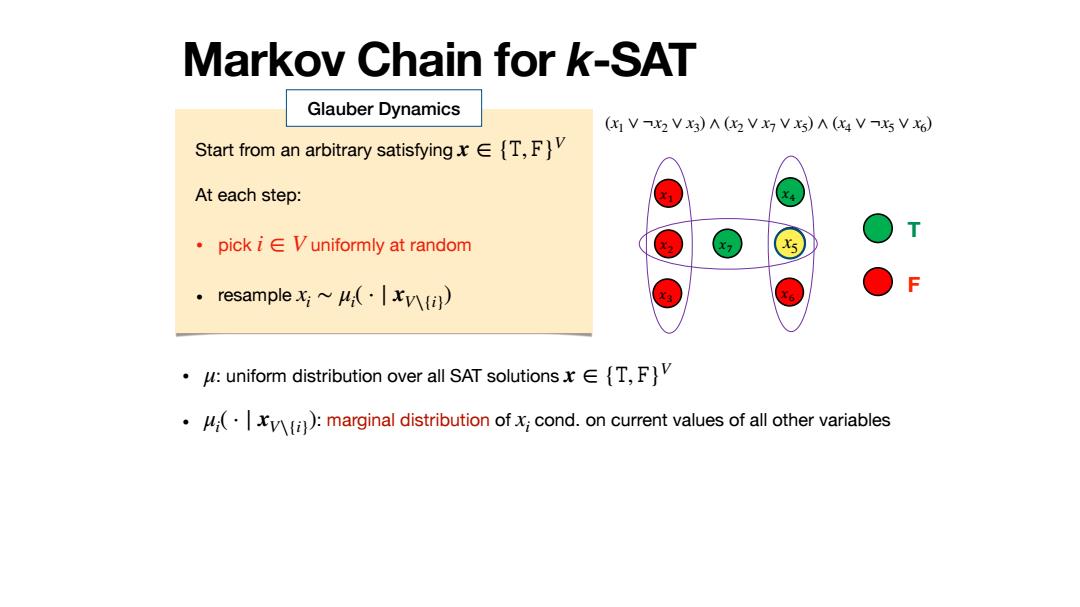
!" !# !$ !% !& !' !( Markov Chain for k-SAT (x1 ∨ ¬x2 ∨ x3) ∧ (x2 ∨ x7 ∨ x5) ∧ (x4 ∨ ¬x5 ∨ x6) T F • : uniform distribution over all SAT solutions • : marginal distribution of cond. on current values of all other variables μ x ∈ {𝚃, 𝙵}V μi ( ⋅ ∣ xV∖{i}) xi x5 Glauber Dynamics Start from an arbitrary satisfying At each step: • pick uniformly at random • resample x ∈ {𝚃, 𝙵}V i ∈ V xi ∼ μi ( ⋅ ∣ xV∖{i})

Markov Chain for k-SAT Glauber Dynamics (X]VX2VX3)A(VXV x5)A (x4 Vx5 VX6) Start from an arbitrary satisfyingx[T,F)V At each step: 。 pick i E Vuniformly at random resamplex:~以·|xi A:uniform distribution over all SAT solutionsx[T,F]V .(marginal distribution ofcond.on current values of all other variables
!" !# !$ !% !& !' !( Markov Chain for k-SAT (x1 ∨ ¬x2 ∨ x3) ∧ (x2 ∨ x7 ∨ x5) ∧ (x4 ∨ ¬x5 ∨ x6) T F • : uniform distribution over all SAT solutions • : marginal distribution of cond. on current values of all other variables μ x ∈ {𝚃, 𝙵}V μi ( ⋅ ∣ xV∖{i}) xi x5 ∈{T, F} Glauber Dynamics Start from an arbitrary satisfying At each step: • pick uniformly at random • resample x ∈ {𝚃, 𝙵}V i ∈ V xi ∼ μi ( ⋅ ∣ xV∖{i})