
Fast Sampling Constraint Satisfaction Solutions via the Lovasz Local Lemma Yitong Yin Nanjing University International Joint Conference On Theoretical Computer Science(IJTCS)2021 融 Frontiers of Algorithmics Workshop(FAW)2021
Fast Sampling Constraint Satisfaction Solutions via the Lovász Local Lemma Yitong Yin Nanjing University International Joint Conference On Theoretical Computer Science (IJTCS) 2021 Frontiers of Algorithmics Workshop (FAW) 2021

Constraint Satisfaction Problem Φ=(V,Q,C) Variables:V={,..}with finite domains ... (local)Constraints:C=[C1,C2,...,Cm} each cC is defined on a subset vbl(c)of variables c:⑧g,→{True,False} iEvbl(c) ·CSP formula:Hx∈Q1×Q2×…×2n x)=∧c(o Example (k-SAT):Boolean variables V=[x1,x2.x3x,} k-CNFΦ=(:1VxV)A(x1VVx4)AxVx4Vx5) clause
• Variables: with finite domains • (local) Constraints: • each is defined on a subset vbl(c) of variables • CSP formula: • Example (k-SAT): Boolean variables V = {x1, x2,…, xn} Q1,…, Qn C = {c1, c2,…, cm} c ∈ C c : i∈ ⨂ 𝗏𝖻𝗅(c) Qi → {𝚃𝚛𝚞𝚎, 𝙵𝚊𝚕𝚜𝚎} ∀x ∈ Q1 × Q2 × ⋯ × Qn Φ(x) = ⋀ c∈C c (x𝗏𝖻𝗅(c)) V = {x1, x2, x3, x4, x5} Φ = (x1 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ ¬x4 ∨ ¬x5) Constraint Satisfaction Problem Φ = (V, Q,C) k-CNF clause

Lovasz Local Lemma (LLL) Variables take independent random values X1,X2,...,X ·Violation Probability:each c∈C is violated with prob.≤p Dependency Degree:each c e C shares variables with s D other constraints c'∈C,i.e.vbl(c)nvbl(c)≠⑦ LLL [Erdos,Lovasz,1975]: epD≤I→solution exists .Constructive LLL [Moser,Tardos,2010]: epD≤I→solution can be found very efficiently
• Variables take independent random values • Violation Probability: each is violated with prob. ≤ p • Dependency Degree: each shares variables with ≤ D other constraints , i.e. • LLL [Erdős, Lovász, 1975]: ⟹ solution exists • Constructive LLL [Moser, Tardos, 2010]: ⟹ solution can be found very efficiently X1, X2,…, Xn c ∈ C c ∈ C c′∈ C 𝗏𝖻𝗅(c) ∩ 𝗏𝖻𝗅(c′) ≠ ∅ epD ≤ 1 epD ≤ 1 Lovász Local Lemma (LLL)
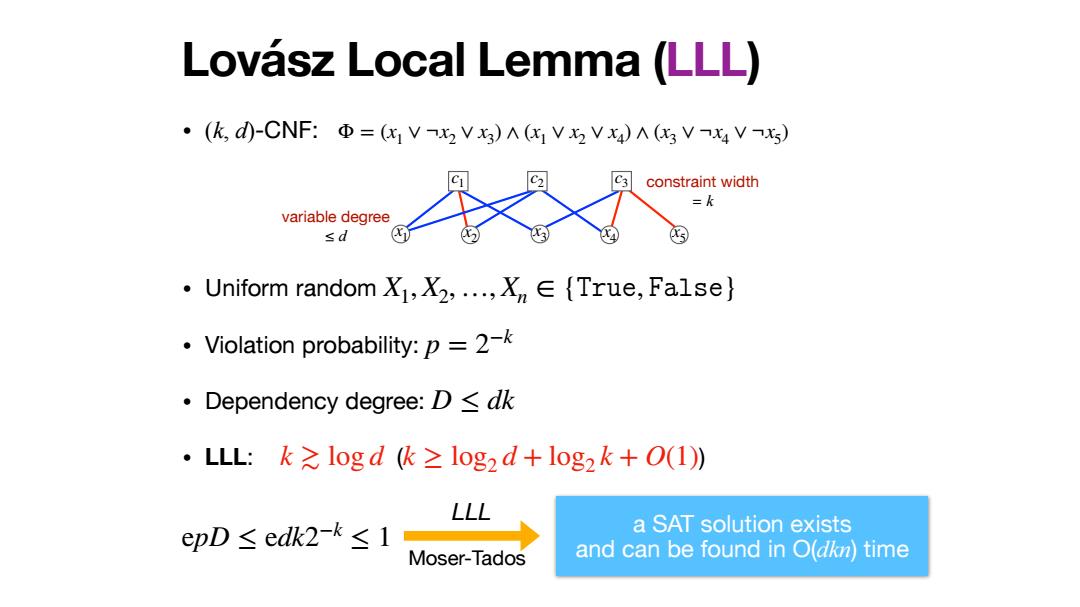
Lovasz Local Lemma(LLL) ·(k,d)-CNF:Φ=(x1Vx2V3)∧(x1Vx2Vx4)A(x3Vx4Vx5) constraint width =k variable degree sd ·Uniform random X1,X,,Xn∈{True,False} Violation probability:p=2-k ·Dependency degree:D≤dk ·LLL:k之logd (k≥1og2d+log2k+O(1) LLL epD≤edk2-k≤1 a SAT solution exists Moser-Tados and can be found in O(dkn)time
Lovász Local Lemma (LLL) • (k, d)-CNF: • Uniform random • Violation probability: • Dependency degree: • LLL: ( ) Φ = (x1 ∨ ¬x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ ¬x4 ∨ ¬x5) X1, X2, …, Xn ∈ {𝚃𝚛𝚞𝚎, 𝙵𝚊𝚕𝚜𝚎} p = 2−k D ≤ dk k ≳ log d k ≥ log2 d + log2 k + O(1) c1 c2 c3 x1 x2 x3 x4 x5 constraint width = k variable degree ≤ d a SAT solution exists and can be found in O(dkn) time epD ≤ edk2−k ≤ 1 LLL Moser-Tados

Sampling Counting Input:a CSP formula =(V,C) Output .(sampling)uniform random satisfying solution .(counting)#of satisfying solutions .u:uniform distribution over all satisfying solutions of Rejection Sampling generate a uniform random Vx∈Q1×Q2×…×2mi if (x)=True then accept else reject; u is the distribution of accept) SAT solutions may be exponentially rare!
• μ: uniform distribution over all satisfying solutions of Φ Sampling & Counting generate a uniform random ; if then accept else reject; is the distribution of ∀x ∈ Q1 × Q2 × ⋯ × Qm Φ(x) = 𝚃𝚛𝚞𝚎 μ (x ∣ accept) Rejection Sampling SAT solutions may be exponentially rare! Input: a CSP formula Output : • (sampling) uniform random satisfying solution • (counting) # of satisfying solutions Φ = (V, Q,C)